Techniques probabilistes, statistiques et analytiques pour les traders

Climax · 26-12-2023 13:43:52

Techniques probabilistes, statistiques et analytiques à connaître pour les traders

Pour les traders, les investisseurs et les acteurs du marché, il est important de comprendre les différentes techniques probabilistes, statistiques et analytiques pour prendre de bonnes décisions lorsque l'avenir est inconnu.

Les marchés sont en grande partie un exercice de probabilité appliquée.

Chacune de ces techniques et méthodes offre des capacités de modélisation uniques et permet aux professionnels de la finance de relever des défis spécifiques et complexes - évaluer les risques et identifier les opportunités potentielles.

Leur application nécessite souvent un mélange de connaissances dans le domaine, de capacités mathématiques et d'expertise informatique.

Elles reflètent la nature interdisciplinaire de l'analyse financière moderne et du développement de stratégies.

Nous décrirons brièvement chacune de ces techniques afin de limiter la longueur de l'article.

Nous disposons d'articles individuels sur un grand nombre des techniques probabilistes, statistiques et analytiques mentionnées ci-dessous, ou du moins de mentions imbriquées dans d'autres articles. Nous ferons donc un lien vers ces articles le cas échéant.

Simulations de Monte Carlo

Cette technique utilise l'échantillonnage aléatoire pour simuler le comportement de systèmes complexes.

Les simulations de Monte Carlo sont utilisées pour fixer le prix de produits dérivés complexes, évaluer les risques (comme la valeur à risque) et simuler divers scénarios de marché.

Elles sont particulièrement utiles pour modéliser des situations où les solutions analytiques sont difficiles ou impossibles à obtenir.

Statistiques bayésiennes

Cette approche incorpore des connaissances antérieures et de nouvelles données pour établir des déclarations probabilistes.

Pour les traders/investisseurs, les statistiques bayésiennes peuvent être utilisées pour mettre à jour les croyances sur les comportements du marché ou la probabilité de divers scénarios économiques sur la base des données entrantes.

Un exemple serait la mise à jour des croyances sur le prix auquel une action devrait être négociée après la publication des résultats trimestriels.

Modèles de Markov

Ces modèles sont utilisés pour prédire la probabilité de divers états en fonction de l'état actuel.

Les modèles de Markov peuvent être appliqués aux transitions des notations de crédit, aux mouvements des prix des actions et aux changements de régime du marché.

Dans d'autres jeux comme les échecs, un modèle de Markov est utilisé pour évaluer la position actuelle pour ce qu'elle est et pour déterminer les meilleures lignes à suivre.

Calcul stochastique

Essentiel pour modéliser le comportement aléatoire des prix des actifs, le calcul stochastique est utilisé dans le modèle Black-Scholes-Merton pour déterminer le prix des options et d'autres produits financiers dérivés.

Il est fondamental pour comprendre les marches aléatoires et le mouvement brownien sur les marchés financiers.

Modèles GARCH (Hétéroscédasticité conditionnelle auto-régressive généralisée)

Ils sont principalement utilisés pour prévoir la volatilité, un facteur dans la gestion du risque et la tarification des produits dérivés.

Les modèles GARCH sont utiles pour modéliser la volatilité variable dans le temps, qui est une caractéristique commune des données financières.

Les modèles eGARCH et tGARCH peuvent être utilisés pour tenir compte des asymétries dans les données de volatilité.

Modèles de copules

Ces modèles sont utilisés pour comprendre et modéliser la structure de dépendance entre différentes classes d'actifs ou instruments financiers.

Les copules sont utiles dans la gestion du risque et pour comprendre les dépendances de queue dans la gestion de portefeuille.

Théorie de la valeur extrême (TVE)

La TVE est utilisée pour évaluer et quantifier le risque de mouvements extrêmes du marché.

Elle est utilisée pour les tests de résistance et la gestion des risques extrêmes dans les portefeuilles.

Analyse des séries temporelles

Des techniques telles que l'ARIMA (Autoregressive Integrated Moving Average) sont utilisées pour prévoir les futurs cours des actions, les indicateurs économiques et d'autres données financières de séries temporelles.

Algorithmes d'apprentissage automatique

Les techniques d'apprentissage automatique telles que la régression, la classification, le regroupement et l'apprentissage par renforcement peuvent être utilisées pour prédire les mouvements du marché, identifier les opportunités de trading et développer des stratégies de trading automatisées.

Arbres de décision et forêts aléatoires

Ils sont utiles pour les tâches de classification et de régression en finance.

Ils peuvent être appliqués à l'évaluation du crédit, à la prédiction de la faillite et à l'élaboration de stratégies de trading quantitatives.

Modèles de Markov cachés (MMC)

Ces modèles sont utilisés pour étudier des données qui évoluent dans le temps - en supposant que les données suivent un modèle dont le comportement est influencé par des facteurs non observables (cachés).

Les MMC sont utiles dans le trading algorithmique pour détecter les changements de régime/paradigme sur les marchés financiers ou pour identifier les facteurs latents qui déterminent les mouvements du marché.

Analyse de survie

Cette approche statistique est utilisée pour prédire le temps qui s'écoulera avant qu'un événement intéressant ne se produise, comme le défaut de paiement d'un produit de crédit.

Utile dans la gestion des risques pour comprendre la durée de vie des instruments financiers ou des investissements.

Par exemple, sur le marché boursier, on conseille souvent "d'investir dans les bonnes entreprises".

Mais la définition d'une "bonne entreprise" (par exemple, ce qui figure dans le Dow Jones ou la capitalisation boursière la plus élevée du S&P 500) change au fil du temps.

Par exemple, les meilleures entreprises d'aujourd'hui sont très différentes de celles d'il y a 30 ans, qui sont très différentes de celles de la génération précédente, et ainsi de suite.

Environ 60 % du S&P 500 est remplacé tous les 25 ans.

Statistiques non paramétriques

Les techniques non paramétriques telles que l'estimation de la densité du noyau et les voisins les plus proches permettent une analyse sans modèle.

Elles peuvent être utiles lorsque la distribution sous-jacente des données financières est inconnue ou complexe.

Réseaux bayésiens dynamiques (RBD)

Il s'agit d'extensions des réseaux bayésiens qui modélisent des séquences de variables.

Ils sont utiles en finance pour modéliser des données séquentielles, comme des séries chronologiques de cours boursiers, et pour faire des prédictions basées sur des tendances historiques.

Filtrage particulaire

Cette méthode est utilisée pour estimer l'état d'une variable cachée dans un système dynamique.

Elle peut être appliquée aux données de trading à haute fréquence pour suivre et prédire les états du marché en temps réel.

Filtres de Kalman

Cet algorithme est utilisé pour estimer l'état d'un système dynamique linéaire à partir d'une série de mesures bruitées.

Les filtres de Kalman sont utilisés pour le suivi adaptatif des marchés et pour l'optimisation des stratégies de trading en temps réel.

Théorie des jeux et équilibres de Nash

La théorie des jeux et les équilibres de Nash sont utilisés pour modéliser et prévoir le comportement des acteurs du marché dans différents scénarios.

Elles sont utilisées dans la prise de décision stratégique et la théorie des enchères.

Théorie de l'utilité

Important pour comprendre et modéliser le comportement des traders et des investisseurs.

Souvent formulée en termes d'aversion au risque et de choix d'investissement dans l'incertitude.

Théorie des graphes et analyse des réseaux

Utile pour modéliser et comprendre l'interconnexion des marchés financiers, le risque systémique et les effets de contagion.

Apprentissage par renforcement

Bien qu'il s'agisse d'une technique d'apprentissage automatique, elle mérite d'être mentionnée pour son utilisation dans le développement d'algorithmes de trading sophistiqués qui apprennent et s'adaptent à partir de leur interaction avec le marché.

Techniques d'optimisation de portefeuille

Des méthodes telles que l'optimisation de la moyenne-variance et l'optimisation stochastique sont utilisées pour construire des portefeuilles efficaces.

Il s'agit principalement du compromis entre le risque et le rendement.

Approches de l'informatique quantique

Les techniques émergentes de l'informatique quantique commencent à être explorées pour la modélisation financière complexe.

Elles offrent des possibilités d'amélioration de la vitesse et de l'efficacité de certains types de calculs.

Mouvement brownien fractionnaire

Il s'agit d'une extension du mouvement brownien classique qui intègre la mémoire dans le processus.

Il est utile pour modéliser les dépendances à long terme dans les séries chronologiques financières, telles que les cours des actions ou les taux d'intérêt.

Réseaux neuronaux et apprentissage profond

Ces techniques d'apprentissage automatique sont utilisées pour la reconnaissance de formes complexes et la modélisation prédictive sur les marchés financiers.

Parmi les exemples d'applications figurent la prédiction du cours des actions, la détection des fraudes et le trading algorithmique.

Méthodes bootstrap

Les techniques de bootstrap sont utilisées pour estimer la distribution d'une statistique (comme la moyenne ou la variance) en procédant à un nouvel échantillonnage avec remplacement à partir des données.

Elles sont utiles en finance pour évaluer l'incertitude des estimations lorsque la distribution sous-jacente est inconnue.

Logique floue

La logique floue est une forme de logique utilisée en informatique qui permet de raisonner avec des informations approximatives ou incertaines - plutôt qu'avec une logique strictement binaire (vrai/faux).

Elle peut être appliquée à l'analyse des investissements et à l'évaluation des risques lorsque les données d'entrée sont ambiguës ou peu claires.

Analyse par vaguelettes

Elle est utilisée pour analyser les données financières de séries temporelles à différentes échelles ou résolutions.

Elle est particulièrement utile pour détecter les modèles cachés, les tendances et les anomalies sur les marchés financiers.

Machines à vecteurs de support (MVS)

Ils sont utilisés pour les tâches de classification et de régression.

Les MVS peuvent être appliqués à l'évaluation du crédit, à la prédiction des marchés et à l'élaboration de stratégies commerciales.

Analyse multifractale

Cette technique est utilisée pour analyser les structures complexes et auto-similaires des séries temporelles financières.

Modélisation basée sur les agents

La modélisation basée sur les agents simule les interactions des agents (comme les investisseurs ou les consommateurs) afin d'évaluer leurs effets sur le système financier dans son ensemble.

Théorie des catastrophes

Utilisée pour étudier le comportement des systèmes qui peuvent subir des changements soudains en réponse à des changements graduels, comme les krachs boursiers ou les crises financières.

Analyse en composantes principales (ACP)

Technique statistique utilisée pour réduire la dimensionnalité des ensembles de données financières tout en conservant la majeure partie de la variabilité des données.

Elle est utilisée dans la gestion des risques et pour identifier les facteurs clés des mouvements du marché.

Modélisation prédictive à l'aide de méthodes économétriques

Des techniques telles que l'auto-régression vectorielle et la cointégration sont utilisées pour prévoir les séries temporelles économiques et financières et pour comprendre les relations entre plusieurs séries temporelles.

Apprentissage automatique quantique

Un domaine émergent qui combine l'informatique quantique et l'apprentissage automatique.

Potentiel pour un traitement et une analyse des données plus rapides et plus efficaces dans le domaine de la finance.

Algorithmes évolutionnaires et programmation génétique

Utilisé pour les problèmes d'optimisation en finance, tels que l'optimisation de portefeuilles et le développement de stratégies, en simulant le processus d'évolution naturelle.

Fait partie d'un sous-ensemble d'algorithmes connus sous le nom d'heuristiques et de métaheuristiques.

Systèmes dynamiques non linéaires et théorie du chaos

Ces approches sont utilisées pour comprendre les systèmes complexes et dynamiques en finance (ceux qui présentent des comportements non linéaires et une sensibilité aux conditions initiales).

Modélisation éparse et techniques de régularisation

Des techniques telles que LASSO (Least Absolute Shrinkage and Selection Operator) et Ridge Regression sont utilisées pour traiter des données de haute dimension en finance.

Elles permettent d'améliorer l'interprétabilité des modèles et d'éviter l'ajustement excessif.

Méthodes d'ensemble

Des méthodes telles que le boosting et le bagging combinent plusieurs modèles pour améliorer les prédictions et réduire la variance.

Utiles pour les prévisions financières et la modélisation des risques.

Analyse des sentiments et traitement du langage naturel

Ces techniques analysent les données textuelles telles que les articles de presse, les rapports financiers et les médias sociaux afin d'évaluer le sentiment du marché et de prédire son impact sur les marchés financiers.

Détection des anomalies

Techniques statistiques permettant d'identifier les valeurs aberrantes ou les anomalies dans les données financières. Elles peuvent être révélatrices d'événements tels que la fraude, la manipulation du marché ou les risques opérationnels.

Modélisation par équations structurelles (MES)

Utilisé pour comprendre les relations complexes entre les variables observées et latentes.

Le MES peut être appliqué pour modéliser les relations entre divers indicateurs économiques et variables de marché.

Statistiques robustes

Se concentre sur les techniques qui ne sont pas indûment affectées par les valeurs aberrantes ou les écarts par rapport aux hypothèses.

Elles conviennent donc aux données financières qui présentent souvent des queues lourdes et sont sujettes à des valeurs aberrantes.

Modèles graphiques et réseaux bayésiens

Ces modèles représentent les dépendances entre les variables et sont utilisés pour l'inférence probabiliste et la prise de décision en finance.

Méthodes d'analyse temps-fréquence

Des techniques telles que la transformée de Fourier à court terme ou la transformée en vaguelettes continue sont utilisées pour analyser les séries temporelles financières non stationnaires.

Algorithmes de trading à haute fréquence

Algorithmes spécialisés conçus pour exécuter des ordres rapidement et en grande quantité.

Utilise des techniques probabilistes et statistiques pour faire des prévisions à court terme sur le marché.

Se concentre sur la microstructure du marché.

Recuit simulé et autres techniques d'optimisation

Utilisé pour résoudre des problèmes d'optimisation complexes dans le domaine de la finance - par exemple, l'allocation d'actifs et l'optimisation de portefeuilles - en particulier lorsque les méthodes traditionnelles sont trop gourmandes en ressources informatiques ou inadéquates.

Résolveurs coniques

Les solveurs coniques sont des outils d'optimisation utilisés pour trouver des solutions à des problèmes mathématiques définis par des sections coniques (comme des cercles ou des ellipses).

Ils impliquent généralement des contraintes et des objectifs.

Les solveurs coniques sont utilisés pour résoudre les problèmes d'optimisation de portefeuille et de gestion des risques, où les contraintes et les objectifs peuvent être modélisés à l'aide de structures coniques.

Fusion de données et intégration de sources multiples

Techniques d'intégration et d'analyse de données provenant de sources multiples (comme les données du marché, les indicateurs économiques et les médias sociaux) afin d'obtenir une vue d'ensemble des marchés financiers.

Modélisation du risque systémique

Méthodes permettant d'évaluer le risque d'effondrement de systèmes ou de marchés financiers entiers, plutôt que de composants individuels.

Comprend l'analyse des réseaux et les tests de résistance.

Complexité algorithmique et théorie de l'information

Utilisée pour analyser la complexité et l'efficacité informationnelle des marchés financiers, et pour développer des stratégies de trading algorithmique.

Traitement des signaux graphiques

Cette méthode étend les concepts de traitement des signaux aux données définies sur des graphiques, tels que les réseaux financiers.

Elle est utile pour comprendre la structure et la dynamique des systèmes financiers et pour le traitement des signaux dans les domaines irréguliers.

Modèles hiérarchiques

Ces modèles structurent les paramètres à plusieurs niveaux, ce qui permet une compréhension et une modélisation plus nuancées des hiérarchies et des relations entre les données - par exemple, celles que l'on trouve dans les portefeuilles multi-actifs.

Voir aussi : Parité des risques hiérarchique

Analyse des données en haute dimension

Des techniques telles que :

l'analyse en composantes principales (ACP)
l'analyse factorielle, et
l'apprentissage multiple...

...sont utilisées pour la réduction de la dimensionnalité et l'extraction de caractéristiques dans des ensembles de données financières de haute dimension.

Méthodes spectrales

Utilisé pour analyser le spectre (valeurs propres) des matrices associées aux données financières.

Ces méthodes sont utilisées pour comprendre diverses propriétés des marchés et des réseaux financiers, y compris la stabilité et le risque du marché.

Modèles de volatilité stochastique

Ces modèles rendent compte de la nature aléatoire et dynamique de la volatilité sur les marchés financiers, ce qui est essentiel pour l'évaluation des produits dérivés et la gestion des risques.

Théorie du contrôle stochastique

Les TCS sont utilisés dans l'optimisation dynamique des portefeuilles et dans la gestion des risques financiers.

Jeux différentiels stochastiques

Un domaine qui combine la théorie des jeux et les processus stochastiques.

Utile pour modéliser les comportements concurrentiels sur les marchés financiers lorsque l'avenir est inconnu.

Théorie stochastique du portefeuille

Cadre mathématique permettant de construire et d'analyser des portefeuilles sur des marchés stochastiques.

Se concentre sur les caractéristiques de distribution des rendements des portefeuilles.

Les personnes qui effectuent ce type d'analyse (par exemple, Monte Carlo) considèrent les résultats en termes de distributions de probabilités.

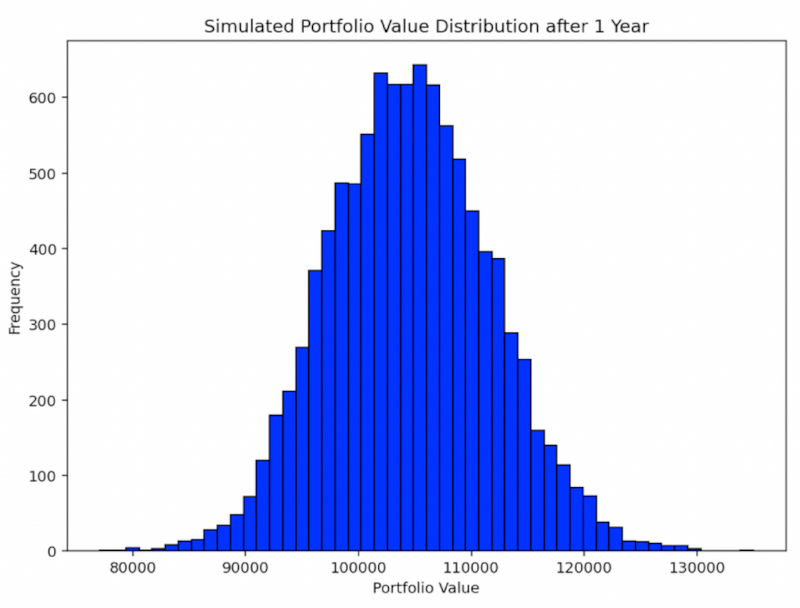
Distribution de probabilité

Les applications avancées et les extensions de la théorie stochastique du portefeuille incluent les effets de la microstructure du marché sur la dynamique du portefeuille.

Optimisation stochastique

Des techniques telles que la descente stochastique du gradient et le recuit simulé sont utilisées pour optimiser les portefeuilles et les stratégies de trading dans un contexte d'incertitude.

Géométrie stochastique

Ce domaine applique les concepts de la géométrie aux processus stochastiques.

Elle peut être utilisée pour modéliser les aspects spatiaux des données financières, par exemple la distribution géographique des acteurs du marché ou des actifs.

Théorie stochastique des jeux

Une généralisation de la théorie des jeux et de la théorie de la décision pour analyser les interactions stratégiques avec des résultats aléatoires.

Analyse fonctionnelle des données (AFD)

Cette approche traite des données qui sont des fonctions (comme des courbes ou des formes) plutôt que des observations scalaires.

Elle peut être utilisée pour analyser des courbes telles que des courbes de rendement ou des trajectoires de prix.

Théorie des systèmes complexes

Cette approche interdisciplinaire étudie la manière dont les relations entre les parties d'un système donnent lieu à ses comportements collectifs et comment le système interagit avec son environnement.

Applicable à l'analyse des systèmes financiers.

Peut également être liée à des techniques telles que la modélisation à base d'agents discutée ci-dessus.

Méthode basée sur les goulets d'étranglement de l'information

Utilisée pour trouver les informations pertinentes dans une variable aléatoire concernant une autre variable aléatoire.

Utile pour la sélection des caractéristiques et la réduction de la complexité des modèles financiers.

Algorithmes métaheuristiques

Des techniques telles que les algorithmes génétiques, le recuit simulé et l'optimisation en essaim sont utilisées pour résoudre des problèmes d'optimisation complexes qui sont difficiles à résoudre à l'aide des méthodes traditionnelles.

Modèles financiers quantiques

Utilisation des principes de la mécanique quantique pour modéliser les marchés financiers.

Ils sont utilisés pour résoudre des problèmes complexes pour lesquels les algorithmes classiques sont inefficaces.

Analyse de séries temporelles non linéaires

Des méthodes telles que la modélisation de l'espace d'état non linéaire et la théorie du chaos sont appliquées pour modéliser et prévoir des dynamiques complexes et non linéaires dans les séries temporelles financières.

Modélisation non linéaire de l'espace d'état

La modélisation non linéaire de l'espace-état est un cadre mathématique permettant de représenter des systèmes dynamiques.

La relation entre les variables et leur évolution dans le temps est caractérisée par des équations non linéaires.

Elle est utilisée pour saisir la dynamique complexe et non linéaire des marchés et des instruments financiers, par exemple pour prédire les cours des actions ou les indicateurs économiques qui ne suivent pas des schémas linéaires directs.

Théorie de la bifurcation

Ce concept mathématique étudie les changements dans la structure qualitative ou topologique d'une famille donnée de modèles.

Utile pour comprendre les changements du marché, comme les transitions entre des périodes stables et des périodes volatiles.

Théorie des grands écarts

Cette branche de la théorie des probabilités fournit un cadre pour l'évaluation des probabilités d'événements rares, tels que les mouvements extrêmes du marché.

Elle est utilisée pour l'évaluation des risques et les tests de résistance.

Analyse topologique des données (ATD)

L'ATD se concentre sur la forme des données et est utilisé pour extraire des structures et des modèles significatifs à partir d'ensembles de données financières complexes (principalement dans des espaces à haute dimension).

Filtrage non linéaire

Des techniques telles que les filtres particulaires et les filtres de Kalman non linéaires sont utilisées pour estimer les états cachés dans les séries temporelles financières.

Elles sont le plus souvent utilisées lorsque la dynamique est non linéaire.

Analyse prédictive à l'aide de l'apprentissage automatique

L'analyse prédictive à l'aide de l'apprentissage automatique implique l'utilisation d'algorithmes sophistiqués (par exemple, les méthodes d'ensemble et l'apprentissage profond) pour analyser les données et faire des prédictions futures basées sur des modèles et des tendances identifiés à partir d'informations (principalement) historiques.

Théorie des réseaux et modèles de contagion financière

Ces méthodes sont essentielles pour comprendre et modéliser l'interconnexion des systèmes financiers et la manière dont les chocs subis par une partie du système peuvent se propager à d'autres.

Modèles de finance comportementale

Ces modèles intègrent les connaissances de la psychologie pour comprendre le comportement des traders/investisseurs et des marchés.

Probabilité quantique

Un domaine émergent qui applique la théorie quantique aux événements probabilistes.

Applications potentielles dans la modélisation des marchés financiers et des systèmes économiques complexes.

Théorie algorithmique des jeux

Combine les algorithmes avec la théorie des jeux pour comprendre et concevoir des systèmes avec de multiples agents intéressés - par exemple, les marchés financiers, les enchères et les stratégies de trading.

Simulation multi-agents

Cette approche simule les actions et les interactions de plusieurs agents afin de recréer et de prédire l'émergence de phénomènes sur les marchés financiers.

Cela ressemble beaucoup à la modélisation basée sur les agents.

Optimisation des fonctions sous-modulaires

Utilisée dans des domaines tels que l'optimisation de portefeuilles et l'allocation de ressources, cette méthode traite de l'optimisation d'une classe spéciale de fonctions fixes qui présentent des rendements décroissants.

Mesures du risque et leurs propriétés

Étude avancée des mesures de risque telles que la CVaR (Conditional Value at Risk) et de leurs propriétés mathématiques, afin de mieux comprendre et gérer les risques financiers.

Modèles factoriels en haute dimension

Ces modèles, y compris l'ACP et l'analyse factorielle, sont étendus à des contextes de haute dimension.

Utile pour l'analyse d'ensembles de données financières à grande échelle, par exemple dans le cadre de l'analyse de données massives (big data).

Parité des risques et méthodes avancées de construction de portefeuille

Au-delà de l'optimisation traditionnelle de la moyenne-variance, les méthodes de parité des risques se concentrent sur la répartition du risque de manière égale entre les composants du portefeuille ou sur un autre objectif d'optimisation - par exemple, équilibrer le risque entre différents environnements macroéconomiques.

Prend en compte les corrélations et les volatilités pour créer des stratégies d'investissement plus résistantes.

Une forme de bêta équilibré.

Les stratégies alpha peuvent également être poursuivies dans le contexte de la parité des risques.

Filtrage adaptatif et apprentissage en finance

Techniques qui mettent à jour de manière adaptative les modèles ou les stratégies en réponse aux nouvelles données du marché.

Elles sont utilisées dans le cadre du trading à haute fréquence et de la prise de décision algorithmique, lorsque les conditions du marché sont en constante évolution.

Hypothèse des marchés fractals

Au-delà de l'hypothèse de l'efficience des marchés, cette approche considère que les marchés financiers sont de nature fractale.

Elle tient compte de l'échelle et de l'auto-similarité des mouvements du marché.

Inférence causale en économétrie

Des techniques telles que les tests de causalité de Granger et les modèles vectoriels auto-régressifs (VAR) sont utilisées pour déduire les relations de cause à effet dans les données économiques.

Elles peuvent être utilisées pour comprendre les impacts de la politique économique et les moteurs du marché.

Différenciation algorithmique en finance

Utilisée pour calculer efficacement les sensibilités des modèles financiers.

Utilisée dans la gestion des risques et l'évaluation des options lorsque des gradients et des dérivées partielles sont nécessaires.

Modèles multi-niveaux en finance

Ces modèles traitent des données organisées à plus d'un niveau.

Un exemple serait des actifs individuels au sein de portefeuilles.

Ils sont utiles pour l'agrégation hiérarchique des risques et les analyses financières à plusieurs niveaux.

Mouvement brownien géométrique dans la modélisation avancée

Au-delà de son application de base dans l'évaluation des options, ce processus stochastique est utilisé pour modéliser les prix des actions dans des scénarios plus complexes, incorporant des sauts et d'autres comportements réels du marché.

Analyse prédictive des séries temporelles avec les réseaux à mémoire à long terme

Un type de réseau neuronal récurrent particulièrement bien adapté à la modélisation et à la prédiction de séquences - par exemple, les données de séries temporelles financières.

Régression quantile

Au-delà des modèles basés sur la moyenne, la régression des quantiles est utilisée pour modéliser les différents quantiles d'une distribution.

Utile pour comprendre l'ensemble des résultats possibles du marché.

Elle peut également être utilisée pour tester la normalité. (La plupart des données financières ont une queue plus grosse que ne le suggère la distribution normale).

Modèles de notation de crédit utilisant l'apprentissage automatique avancé

Incorporation de techniques telles que les forêts aléatoires, le gradient boosting et les réseaux neuronaux pour améliorer la précision de l'évaluation du risque de crédit.

Analyse de la microstructure du marché

Comprendre les mécanismes et les comportements des marchés financiers au niveau microéconomique, notamment les spreads entre l'offre et la demande, le flux d'ordres et la liquidité.

Modélisation du risque de contrepartie

Évaluation du risque de défaillance de l'autre partie à une transaction financière.

Utilise des modèles qui tiennent compte des corrélations et des effets de réseau.

Calibration des processus stochastiques en finance

Techniques d'étalonnage des modèles stochastiques en fonction des données du marché.

Permet de s'assurer que les modèles reflètent correctement les dynamiques de marché observées.

Techniques avancées d'évaluation des produits dérivés

Au-delà de Black-Scholes, utilisation de modèles de volatilité stochastique, de modèles de diffusion par sauts et d'autres méthodes avancées pour évaluer des produits financiers dérivés complexes.

Apprentissage par différence temporelle dans l'apprentissage par renforcement

Appliqué au trading algorithmique et à la gestion de portefeuille.

Aide à l'apprentissage de politiques optimales par échantillonnage, sans nécessiter de modèle de l'environnement.

Modélisation avancée du risque de crédit

Utilisation de l'analyse de survie, de modèles d'aléas et de l'apprentissage automatique pour prédire les défaillances et gérer le risque de crédit avec plus de précision.

Important dans le contexte de grands portefeuilles de crédit.

Processus stochastiques avec sauts

Au-delà des modèles à trajectoires continues, ces processus (comme les processus de saut de Poisson) modélisent les mouvements soudains des prix du marché.

Ils sont utiles pour saisir les chocs du marché et les risques extrêmes.

Mécanique statistique de non-équilibre en finance

Application des concepts de la physique aux marchés financiers afin de modéliser et de comprendre la dynamique des marchés loin de l'équilibre, comme lors des krachs ou des bulles.

Techniques de gestion des risques extrêmes

Des méthodes avancées telles que les tests de résistance, l'analyse de scénarios et la couverture des risques extrêmes sont utilisées pour gérer et atténuer les risques liés aux mouvements extrêmes du marché.

Modèles de copules à haute dimension

Extension de la modélisation par copules à des dimensions élevées pour comprendre et modéliser les dépendances dans de grands portefeuilles ou entre plusieurs instruments financiers.

Modélisation du risque de liquidité

Méthodes avancées de quantification et de gestion du risque de liquidité. Particulièrement important en période de crise financière.

Modèles de réseaux dans l'analyse du risque systémique

Utilisation de la théorie des graphes et des modèles de réseaux pour analyser et atténuer le risque systémique dans le système financier, y compris l'étude des effets de contagion et de l'interconnexion.

Techniques de gestion de l'actif et du passif

Approches de modélisation avancée pour optimiser la composition des actifs et des passifs.

Utilisées par les banques, les compagnies d'assurance et de réassurance pour gérer les risques et les rendements au fil du temps.

Modélisation des données financières à haute fréquence

Techniques de traitement et d'analyse des volumes massifs de données générés par le trading à haute fréquence.

L'accent est mis sur la microstructure du marché et la dynamique des prix intrajournaliers.

Économie comportementale et expérimentale dans la prise de décision financière

Application des connaissances de l'économie comportementale pour comprendre et prédire la prise de décision financière, les résultats du marché et les anomalies.

Méthodes bayésiennes informatiques en finance

Utilisation de l'inférence bayésienne et des techniques de Markov Chain Monte Carlo (MCMC) pour une modélisation plus complexe et plus réaliste des phénomènes financiers.

Optimisation multi-objectifs en finance

Techniques d'optimisation de multiples objectifs contradictoires, tels que le rendement et le risque, la liquidité et le rendement, dans la gestion des investissements et des portefeuilles.

On parle parfois d'optimisation à moment élevé lorsque l'on essaie de trouver un équilibre ou d'optimiser diverses mesures au-delà de la moyenne (rendement) et de la variance (volatilité) - par exemple, l'asymétrie et l'aplatissement.

Conclusion

Chacune de ces techniques a son propre domaine d'application et convient à des types spécifiques d'analyse financière.

Le choix d'une technique dépend largement de la nature du problème financier, du type de données disponibles et des objectifs spécifiques de l'analyse.

La compréhension et l'application de ces méthodes probabilistes peuvent améliorer les capacités d'analyse des traders et des investisseurs.

Elles permettent aux acteurs du marché

d'affiner leurs stratégies
d'améliorer leurs modèles prédictifs et
de prendre des décisions plus éclairées dans un environnement caractérisé par un grand nombre d'inconnues et de dimensions.

#1 26-12-2023 13:43:52