Comment mesurer les niveaux de risques des marchés avec la VaR et la CVaR

La quantification du risque est devenue l'une des plus grandes préoccupations (ou du moins devrait l'être) des traders. La volatilité des actions, des taux de change, des taux d'intérêt, etc. ont rendu l'étude du risque de plus en plus importante. Dans cet article, nous vous montrerons comment utiliser la VaR et la CVaR pour évaluer vos niveaux de risque avec un degré de précision élevé.

Une autre question importante qui nous a permis d'améliorer l'étude du risque, parmi celles associées à notre activité, a été l'augmentation exponentielle de la capacité de calcul dont nous disposons actuellement. Actuellement, en tant que trader, vous avez au bout des doigts, depuis votre ordinateur portable ou votre smartphone, des bases de données contenant toutes les informations nécessaires sur l'historique des prix de presque tous les actifs financiers.

Lorsque nous développons une stratégie ou un système de trading, nous ne devons pas seulement nous concentrer sur l'établissement de règles claires pour entrer et sortir du marché, mais nous devons également analyser objectivement les résultats de notre système de trading.

Pour parvenir à une analyse objective, une grande variété de mesures a été mise au point pour évaluer les différents aspects de notre activité. Dans cet article, nous vous apprendrons à utiliser deux mesures basées sur le contrôle des risques : La valeur à risque (VaR) et la valeur conditionnelle à risque (CVaR). Ces mesures d'évaluation des risques ont des méthodologies et des techniques différentes pour leur estimation.

Avant d'entrer directement dans leur étude, il est important d'avoir quelques notions de base, comme par exemple ce qu'est le risque financier et quels sont les types de risques.

Qu'est-ce que le risque financier ?

Dans le contexte de l'investissement, le risque est la probabilité de perte due à des événements qui peuvent produire des changements importants, et qui affectent un actif financier. Il est donc important que lorsque nous décidons de faire un investissement, nous identifions et quantifions les différents types de risques auxquels nous serons exposés lors de l'investissement.

Tous les investissements comportent un risque associé, mais lorsque nous le gérons bien, nous pouvons trouver de grandes possibilités de rendements importants. Vous avez sûrement entendu parler de "l'aversion au risque". L'aversion au risque fait référence à l'attitude ou à la préférence d'un investisseur pour éviter l'incertitude financière ou le risque. Cela l'amène à investir dans des actifs financiers plus sûrs, même s'ils sont moins rentables.

Types de risques financiers

Bien qu'il existe de nombreux risques dans le monde de l'investissement, le risque financier peut être classé en trois grandes catégories :

Le risque de marché : ce type de risque se réfère au risque de perte résultant des mouvements de prix d'un actif financier ou du marché en général.

Le risque de crédit : l'incapacité d'une partie à répondre aux obligations d'une émission ou aux conditions strictes de l'émission (montant, intérêts, etc.), ce qui entraîne une perte pour la contrepartie.

Risque opérationnel : Ce type de risque est défini comme un risque de perte dû à des insuffisances ou à des défaillances des processus, du personnel et des systèmes internes.

Maintenant que nous avons clarifié ces concepts de base, voyons ce que sont la VaR et la CVaR.

Valeur à risque (VaR)

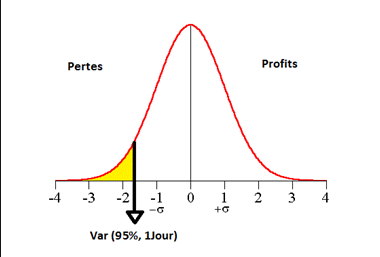
La valeur à risque est une mesure statistique utilisée pour évaluer le risque d'une position d'un actif ou d'un portefeuille donné. La VaR est la perte maximale attendue, dans des conditions normales de marché, dans un portefeuille ou un système de trading, avec une probabilité (généralement de 1 ou 5 %) et un intervalle de temps connu (généralement un jour, une semaine ou un mois).

La VaR est mesurée par trois variables : le montant de la perte, la probabilité qu'une telle perte se produise (niveau de confiance) et l'intervalle de temps dans lequel elle se produit. Il est important de noter que la VaR ne cherche pas à décrire ou à prévoir les pires scénarios, mais plutôt à fournir une estimation de la gamme des gains ou pertes potentiels.

Méthodes de calcul de la VaR

Il existe trois grandes méthodes ou approches pour calculer la VaR :

Méthode paramétrique : lorsque nous calculons la VaR à l'aide de la méthode paramétrique, nous supposons que la rentabilité a une distribution normale et que le portefeuille est une fonction linéaire des facteurs. Pour le calcul paramétrique, il est nécessaire de disposer des principaux paramètres statistiques (moyenne, variances, covariance, écarts types, etc.) de l'actif financier ou du portefeuille que nous analysons.

La formule de calcul de la VaR selon la méthode paramétrique est la suivante :

VaR = F * S * σ *

Où :

F = Valeur déterminée par le niveau de confiance (également appelée valeur Z).

S = Montant du portefeuille ou de l'actif financier aux prix courants du marché.

σ = Écart-type des rendements des actifs.

t = Horizon temporel dans lequel la VaR doit être calculée.

Méthode de simulation historique : utilise une grande quantité de données historiques pour estimer la VaR, mais ne fait aucune hypothèse sur la distribution de probabilité. L'une des plus grandes limites de cette approche est qu'elle suppose que toutes les variations futures possibles des prix des actifs ont déjà été observées dans le passé. La valeur de la VaR dépendra de la source des données et de la taille de la série (période de temps des données).

Modèle VaR de Monte-Carlo : Le calcul de la VaR selon la méthode de Monte-Carlo est basé sur la génération de centaines ou de milliers de scénarios hypothétiques à partir des séries de données initiales saisies par l'utilisateur. La précision de la VaR dépendra du nombre de scénarios que nous simulerons. La validation du modèle est fondamentale, pour cela il est recommandé d'effectuer des tests de backtest pour vérifier que la VaR estimée est vérifiée avec les séries historiques.

Un exemple pratique de calcul de la VaR :

Je vais le faire en donnant un exemple de calcul de la VaR dans les actions visant à simplifier le calcul des pips et des lots :

Supposons que nous ayons un portefeuille composé de 1000 actions de la société ABC et que le prix actuel par action soit de 12$, l'écart-type quotidien est de 1,8%. Comment pouvons-nous calculer la VaR avec un niveau de confiance de 95% pour une journée ?

La formule de calcul de la VaR est la suivante :

VaR = F * S * σ *

Pour calculer la valeur de F, nous utilisons la fonction "DISTR.NORM.ESTAND.INV (probabilité)" du tableur Excel.

F = DISTR.NORM.ESTAND.INV (niveau de confiance) = DISTR.NORM.ESTAND.INV (95%) = 1,6448

S est le montant total investi dans le portefeuille et est calculé comme suit :

S = montant de l'action * prix du marché = 1.000 actions * 12$ = 12.000

L'écart-type σ est égal à 1,8 %.

Comme nous voulons calculer la VaR pour un jour, alors t = 1.

Nous remplaçons les valeurs dans la formule VaR et nous avons :

VaR = 1,6448 * 12

Cette valeur de la VaR nous indique que l'investisseur a un niveau de confiance de 95% que son investissement ne perdra pas plus de 355,28 dollars en un jour.

Que se passe-t-il si nous augmentons le niveau de confiance à 99 % ? Dans ce cas, la VaR serait :

VaR = 2,3263 * 12 000 $* 1,8 % * = 502,48

Cette valeur de la VaR nous indique que l'investisseur a un niveau de confiance de 99 % dans le fait que son investissement ne perdra pas plus de 502,48 dollars en une journée, ou, ce qui est identique, la probabilité de subir des pertes supérieures à 502,48 dollars au cours d'une journée, n'est que de 1 %.

Avantages de la VaR

Quelques avantages très importants de l'utilisation de la VaR pour la quantification du risque financier sans ce qui suit :

- La VaR est une mesure de risque standardisée très reconnue par les opérateurs et les régulateurs. Elle est devenue une norme dans le secteur financier.

- Elle ajoute tout le risque d'un investissement en un seul chiffre, ce qui rend l'évaluation du risque très facile.

- Elle est probabiliste et nous fournit des informations utiles sur les probabilités associées (niveau de confiance) à un montant spécifique de pertes (perte maximale).

- Elle peut être appliquée à tout type de gestion et permet également de comparer les risques de différents portefeuilles quelle que soit leur composition, qu'il s'agisse de titres à revenu fixe ou d'actions.

- La VaR vous permet d'ajouter les risques de différentes positions en tenant compte de la manière dont elles sont corrélées entre elles, des différents facteurs de risque.

- Elle prend en compte de multiples facteurs de risque et peut se concentrer non seulement sur des composantes individuelles, mais aussi sur le risque global de l'ensemble du portefeuille.

- Elle est plus simple et plus facile à comprendre que les autres indicateurs qui mesurent le risque financier, car elle est exprimée en perte d'argent (monnaie de base ; dollar, euro, etc.).

Inconvénients de la VaR

Mais la VaR, comme toute autre mesure utilisée pour les systèmes d'investissement, a ses inconvénients :

- Elle dépend généralement de la qualité des données historiques utilisées pour son calcul. Si les données incluses ne sont pas exactes ou correctes, la VaR ne sera pas utile.

- Bien que l'interprétation des valeurs de la VaR soit très simple, certaines méthodes de calcul peuvent être très compliquées et coûteuses, par exemple la méthode de Monte Carlo.

- Elle peut générer un faux sentiment de sécurité chez les traders. Toute mesure de probabilité ne doit pas être interprétée comme une certitude de ce qui va se passer. N'oubliez pas qu'en tant que traders, nous ne traitons que des scénarios d'incertitude, jamais des scénarios de certitude, nous ne faisons pas de prévisions.

- Elle ne calcule pas le montant de la perte attendue restant dans le pourcentage de probabilité.

Valeur en risque conditionnelle (CVaR)

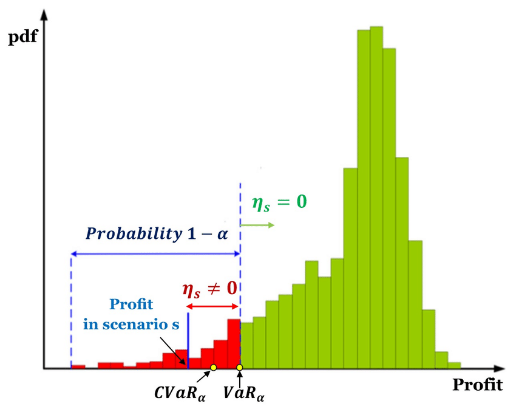
La valeur du risque conditionnel (CVaR) est la moyenne des observations dans la file de distribution, c'est-à-dire en dessous de la VaR au niveau de confiance spécifié. Par conséquent, la CVaR est également connue sous le nom de déficit attendu (Expected Shortfall, ES), AVaR (Average Value at Risk) ou ETL (Expected Tail Loss).

La CVaR est le résultat de la moyenne pondérée des observations pour lesquelles la perte dépasse la VaR. Par conséquent, la CVaR dépasse l'estimation de la VaR, car elle permet de quantifier des situations plus risquées, complétant ainsi les informations fournies par la VaR.

La CVaR est utilisée pour l'optimisation des portefeuilles, car elle quantifie les pertes qui dépassent la VaR et sert de limite supérieure à la VaR.

Propriétés du CVaR

La CVaR se distingue par de meilleures propriétés mathématiques que la VaR, étant une mesure cohérente du risque, car elle répond aux critères de :

Monotonicité : Si un actif financier est plus performant qu'un autre sur un horizon de temps donné, son risque est également plus faible.

Homogénéité positive : Désigne la proportionnalité entre la taille de la position et le risque.

Invariance aux transferts : En ajoutant du capital à une position, votre risque diminue en proportion directe du capital ajouté.

Sous-additivité : La diversification des actifs diminue le risque d'une position globale.

En résumé, la CVaR mesure si le risque de deux ou plusieurs actifs qui composent un portefeuille est inférieur à la somme des risques individuels.

Interprétation de la valeur conditionnelle à risque (CVaR)

Le choix entre la CVaR et la VaR n'est pas toujours simple, puisque la valeur à risque conditionnelle (CVaR) est dérivée de la valeur à risque (VaR). En général, l'utilisation de la CVaR plutôt que de la seule VaR tend à conduire à une approche plus conservatrice en termes d'exposition au risque.

Alors que la VaR représente une perte maximale associée à une probabilité et à un horizon temporel définis, la CVaR est la perte attendue si l'on franchit le seuil de la pire éventualité (perte maximale). En d'autres termes, la CVaR quantifie les pertes attendues qui se produisent au-delà du point de rupture de la VaR.

En règle générale, si un investissement a maintenu sa stabilité dans le temps, la valeur de risque pourrait être suffisante pour la gestion du risque dans un portefeuille qui maintient l'investissement actif. Toutefois, nous devons garder à l'esprit que moins l'investissement est stable, plus il y a de chances que la VaR n'affiche jamais une image complète du risque. Dans la pratique, les systèmes de trading dépassent rarement la VaR de manière significative. Toutefois, les systèmes plus volatils peuvent présenter une CVaR plusieurs fois supérieure à la VaR.

Enfin, si nous créons un système de trading et calculons votre la VaR, cette VaR nous indique quelle est la perte maximale avec un certain niveau de confiance et un certain horizon temporel. Mais si la perte est supérieure à la VaR, combien devons-nous nous attendre à perdre ? C'est là qu'entre en jeu la valeur à risque conditionnelle (CVaR), qui nous indiquera la perte moyenne conditionnelle attendue si la perte est supérieure à la VaR.

Comparatif des courtiers en bourse

Courtiers	Supports financiers	Frais de courtage Actions Euronext	Notre avis
	Compte titres, compte sur marge	Pas de commissions pour un volume mensuel maximum de 100 000 EUR puis 0,20%	XTB : Trading sans commissions, mais avec un choix de titres limité à 3500 actions et 400 ETF. Compte démo gratuit pour tester la plateforme.
	Compte titres, PEA, PEA-PME, banque en ligne	0.10% à 0.20% selon le profil	Service complet avec toutes les options d'une banque en ligne
	Compte Titres	1€ par ordre	Trade Republic est accessible à tous les investisseurs avec une application mobile élégante et aucun dépôt minimum. Toutefois, l'accent mis sur le trading mobile limite les outils d'analyse.
Investir comporte des risques de perte