Théorie des probabilités et trading

- Hasard
- Exclusivité mutuelle
- Expérience (Essai de Bernoulli)
- Distribution de probabilités
- Distribution binomiale
- Valeur attendue
- Chaîne de Markov
- Marche aléatoire
- Processus stochastique
- Probabilité conditionnelle
- Loi des grands nombres
- Théorème de Bayes
- Corrélation et covariance
- Brokers de CFD
- FAQ
- Conclusion - La théorie des probabilités dans le trading
La théorie des probabilités est essentielle en matière de trading et d'investissement car elle permet aux acteurs du marché de comprendre et de quantifier l'incertitude et le risque associés aux décisions financières.
Comme la vie elle-même, le trading est une question de probabilités. Il existe rarement des résultats évidents, en noir et blanc, sur lesquels il est facile de capitaliser.
En utilisant la théorie des probabilités, les traders/investisseurs peuvent prendre des décisions plus éclairées sur la base de la probabilité de divers résultats.
Voici quelques raisons pour lesquelles la théorie des probabilités est si importante dans le trading/investissement :
Quantifier le risque
La théorie des probabilités permet aux investisseurs de calculer la probabilité que diverses choses se produisent, y compris les scénarios positifs et négatifs.
Cela permet aux traders de mieux comprendre les risques potentiels associés à différentes transactions/investissements.
Prise de décision
La théorie des probabilités permet aux traders de prendre de meilleures décisions en se basant sur la probabilité de différents résultats et en évaluant les probabilités elles-mêmes (ce que l'on pourrait appeler des "probabilités de probabilités", car les chances que différentes choses se produisent ne sont pas connues elles-mêmes).
Par exemple, si un investissement ou une transaction a une probabilité de 70 % de produire un rendement positif sur un an, comment le savez-vous ?
La théorie des probabilités couvre des aspects tels que la variance et la manière de mieux gérer ce que vous ne savez pas et ne pouvez pas savoir.
Gestion de portefeuille
La théorie des probabilités aide les traders/investisseurs à gérer leurs portefeuilles en leur fournissant un moyen d'évaluer le risque associé à différentes classes d'actifs.
En analysant la probabilité de différents résultats, les traders/investisseurs peuvent créer un portefeuille diversifié qui équilibre le risque et le rendement.
Gestion du risque
La théorie des probabilités est également importante dans la gestion des risques, car elle aide les investisseurs à déterminer la probabilité d'événements susceptibles d'avoir un impact négatif sur leurs investissements/opérations et à prendre des mesures pour les atténuer.
Dans l'ensemble, la théorie des probabilités est un outil important qui permet aux investisseurs/traders de comprendre les risques et les bénéfices potentiels de différentes opportunités d'investissement, de faire des choix plus éclairés et d'obtenir de meilleurs résultats sur le long terme.
Dans cet article, nous allons examiner les différentes branches de la théorie des probabilités et ses applications dans le domaine du trading.
Hasard
Dans la théorie des probabilités, le caractère aléatoire fait référence au fait que l'issue d'un événement est imprévisible et peut varier d'un essai à l'autre.
Ce phénomène est souvent modélisé à l'aide de distributions de probabilité, qui décrivent la probabilité de chaque résultat possible.
L'aléatoire est un concept fondamental de la théorie des probabilités, car il nous permet de quantifier ce qui est inconnu et de faire des prédictions sur l'avenir à partir d'informations incomplètes.
Dans de nombreuses situations du monde réel, les résultats des événements sont affectés par un grand nombre de variables qu'il est difficile, voire impossible, de prévoir avec certitude/précision.
L'aléatoire permet d'en tenir compte et d'estimer la probabilité de divers résultats sur la base de données historiques, de liens de cause à effet économiques ou d'autres informations.
Dans le domaine du trading et de l'investissement, le hasard est toujours présent car les marchés financiers sont soumis à un large éventail d'influences.
Il existe de nombreux types de personnes sur les marchés, de tailles différentes, et dont les motivations pour effectuer des transactions sont différentes.
Le caractère aléatoire peut se manifester sous la forme de la volatilité du marché, d'événements inattendus ou d'autres facteurs susceptibles de provoquer des fluctuations rapides et imprévisibles des prix.
Il est essentiel de comprendre et de prendre en compte ce caractère aléatoire pour élaborer des stratégies de trading fructueuses et gérer les risques.
Plus les gens acquièrent de l'expérience sur les marchés, plus ils se rendent compte que tout ce qu'ils savent est faible par rapport aux choses qu'il faut savoir en fonction de ce qui est actualisé sur les marchés.
L'une des façons dont les traders et les investisseurs peuvent gérer le caractère aléatoire est d'utiliser des modèles basés sur les probabilités pour prendre des décisions.
Par exemple, un trader peut utiliser un modèle statistique pour estimer la probabilité d'une hausse ou d'une baisse du prix d'un actif particulier sur une période donnée. Ces informations peuvent ensuite être utilisées pour constituer un portefeuille bien équilibré et gérer le risque.
Par exemple, si la distribution des prix actualisés d'un actif particulier ressemble à ceci :
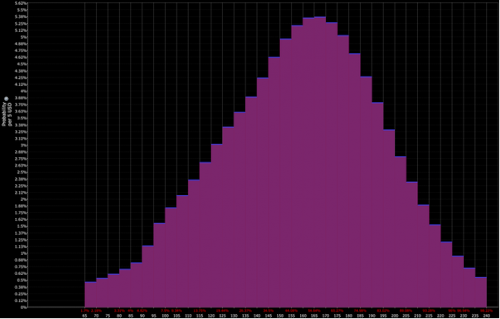
Et l'interprétation du trader est plus proche de la combinaison de la distribution rouge et violette (c'est-à-dire une inclinaison baissière) :
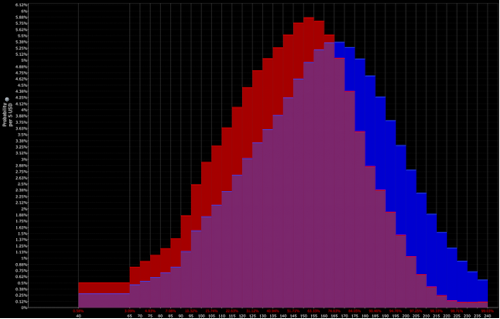
Ils peuvent alors s'attendre à prendre une position baissière sur l'actif. Ensuite, bien sûr, il y a la question de la manière de la mettre en place et de la taille.
Exclusivité mutuelle
En théorie des probabilités, le concept d'exclusivité mutuelle fait référence à la propriété de deux événements qui sont différents l'un de l'autre.
Mathématiquement, deux événements A et B sont dits mutuellement exclusifs si leur intersection (c'est-à-dire l'événement où A et B se produisent tous les deux) est vide, c'est-à-dire que P(A ∩ B) = 0.
L'exclusivité mutuelle est importante dans le trading/investissement car elle aide les investisseurs à mieux comprendre comment gérer leurs risques.
Lorsque les investisseurs détiennent un portefeuille d'actifs, ils doivent tenir compte des corrélations entre/parmi leurs actifs.
Par exemple, supposons qu'un trader/investisseur possède un portefeuille d'actions comprenant à la fois des sociétés technologiques et des sociétés pétrolières. Si le prix du pétrole augmente, cela peut aider les compagnies pétrolières mais les valeurs technologiques peuvent en pâtir (par exemple, en raison de l'effet négatif de la hausse des prix du pétrole sur les taux d'intérêt), et vice versa.
Toutefois, si certains développements se produisent dans chaque secteur, ils peuvent ne pas avoir d'influence sur les prix des titres de l'autre secteur.
Ainsi, même si les titres sont liés les uns aux autres à certains égards - comme les variations de la croissance actualisée et de l'inflation - à d'autres égards, ils s'excluent mutuellement.
Comment ces facteurs mutuellement exclusifs sont-ils séparés ?
Parfois, il s'agit simplement de la nature du flux financier - par exemple, le pétrole par rapport aux produits/services technologiques.
Parfois, on les appelle des facteurs - par exemple, momentum, taille, qualité, valeur, etc.
En outre, l'exclusivité mutuelle est importante dans le trading des options, où le gain d'une option peut souvent être basé sur la non-occurrence d'un autre événement. Dans ce contexte, l'exclusivité mutuelle aide les opérateurs à couvrir leurs risques et à gérer leur exposition.
Expérience (Essai de Bernoulli)
Une expérience ou un essai de Bernoulli est un concept fondamental de la théorie des probabilités qui fait référence à un événement aléatoire avec seulement deux résultats possibles.
Par exemple, le lancer d'une pièce de monnaie est un essai de Bernoulli, où les résultats possibles sont pile ou face.
Un autre exemple est de savoir si une transaction d'option particulière sera payante (dans le cours) ou non (hors du cours) à l'expiration.
Dans la théorie des probabilités, la probabilité de réussite (c'est-à-dire l'issue qui nous intéresse) est définie par p, et la probabilité d'échec (c'est-à-dire l'autre issue) par q = 1 - p.
Les résultats d'un essai de Bernoulli sont souvent désignés par 1 pour le succès et 0 pour l'échec.
L'importance des essais de Bernoulli dans le domaine du trading et de l'investissement réside dans le fait que certaines décisions financières impliquent des résultats binaires.
Par exemple, vous pouvez décider d'acheter une option d'achat d'actions en espérant qu'elle atteindra le seuil de rentabilité, ou vous pouvez choisir de la vendre en espérant que son prix atteindra le seuil de rentabilité et que vous percevrez la totalité de la prime.
Dans les deux cas, le résultat est binaire en termes d'argent. Les paris binaires purs se présentent sous la forme d'options binaires.
En appliquant les principes de la théorie des probabilités au trading et à l'investissement, vous pouvez prendre des décisions plus éclairées sur le moment d'acheter ou de vendre.
Il existe également des concepts tels que la valeur attendue, qui vous apprennent à ne pas toujours parier sur le résultat le plus probable.
Distribution de probabilités
En théorie des probabilités, une distribution de probabilité est une fonction qui décrit la probabilité de différents résultats dans une expérience ou un processus aléatoire.
Elle spécifie les probabilités de toutes les issues possibles d'un événement, et la somme des probabilités de toutes les issues est égale à un.
Il existe de nombreux types de distributions de probabilité, mais parmi les plus courantes figurent la distribution normale, la distribution binomiale et la distribution de Poisson.
Chaque distribution possède son propre ensemble de paramètres qui déterminent sa forme, et ces paramètres sont souvent utilisés pour faire des prédictions et prendre des décisions.
Bien sûr, sur les marchés financiers, les rendements ont tendance à avoir des queues plus larges et à ne pas correspondre à une distribution préétablie, ils ont donc tendance à être personnalisés.
Dans l'ensemble, les distributions de probabilité sont importantes car elles fournissent un cadre permettant de comprendre le risque et l'incertitude associés aux investissements financiers.
L'un des concepts les plus importants en matière de trading/investissement est que tout est une probabilité (c'est-à-dire une distribution de résultats potentiels). Il n'existe pas d'issue unique particulièrement probable.
En utilisant des distributions de probabilité, les traders et les investisseurs peuvent estimer la probabilité de différents résultats et prendre des décisions plus éclairées sur la manière d'allouer leurs ressources.
Par exemple, un trader peut utiliser la distribution normale ou une distribution à queue plus grosse pour modéliser les rendements quotidiens d'une action particulière.
Il pourrait ensuite utiliser cette distribution pour estimer la probabilité que le rendement de l'action dépasse un certain seuil, par exemple un rendement de +/-5 % en un jour.
En utilisant les distributions de probabilités de cette manière, les traders peuvent mieux gérer leur risque et optimiser leurs rendements.
Outre l'estimation des probabilités, les distributions de probabilités sont également utilisées pour créer des instruments financiers tels que les options et les contrats à terme.
Ces instruments ont un prix basé sur la distribution sous-jacente de l'actif auquel ils sont liés, et les traders peuvent les utiliser pour couvrir leur risque ou faire des paris sur les mouvements de prix futurs de l'actif.
De plus, les distributions peuvent être construites sur la base du prix des options sous-jacentes, comme on peut le voir ci-dessous.
Distribution telle qu'actualisée par les marchés :
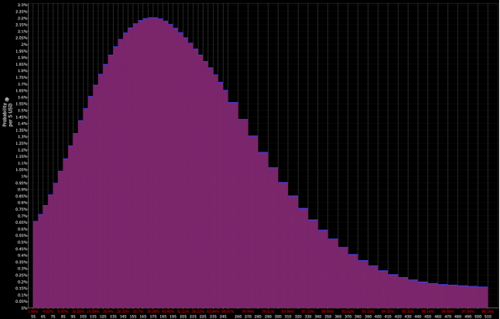
Distribution déterminée par le trader (ce qui ouvre la porte à des opportunités tactiques) :
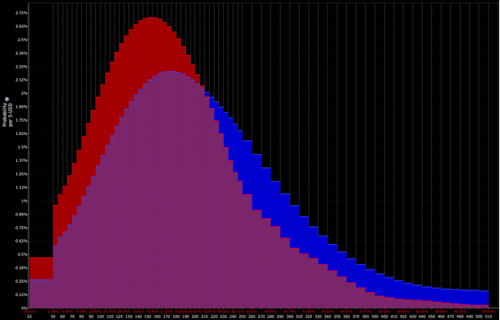
Distribution binomiale
La distribution binomiale est une distribution de probabilité qui modélise le nombre d'issues positives dans une série d'essais indépendants et identiques, où chaque essai n'a que deux issues possibles (par exemple, pile ou face, gagnant ou perdant, haut ou bas).
Les paramètres clés de la distribution binomiale sont la probabilité de réussite d'un seul essai (désignée par p) et le nombre d'essais (désigné par n).
La distribution binomiale est importante dans le domaine du trading et de l'investissement car elle peut être utilisée pour modéliser la distribution des rendements d'une stratégie de trading binaire (par exemple, une stratégie qui consiste à acheter ou à vendre un actif selon qu'un certain événement se produit ou non).
En particulier, la valeur attendue d'une stratégie de trading binaire peut être calculée en utilisant la distribution binomiale.
La valeur attendue d'une stratégie de trading binaire est la somme des produits de la probabilité de chaque résultat possible et du rendement correspondant à ce résultat.
Par exemple, si une stratégie de trading binaire a une probabilité de 60% de réaliser un rendement de 10% et une probabilité de 40% de réaliser un rendement de -5%, la valeur attendue de la stratégie est la suivante :
(0.6 * 0.1) + (0.4 * (-0.05)) = +0.04
La distribution binomiale peut être utilisée pour calculer les probabilités de chaque résultat possible dans une série de transactions binaires.
Par exemple, si un trader effectue 10 transactions binaires avec une probabilité de réussite de 60 % et une probabilité d'échec de 40 %, la probabilité de réaliser un certain nombre de transactions réussies (c'est-à-dire un certain taux de réussite) peut être calculée à l'aide de la distribution binomiale.
Cela peut aider le trader à évaluer le risque et le rendement potentiel de sa stratégie de trading.
Valeur attendue
Nous avons abordé la valeur attendue (VA) dans d'autres articles, car il s'agit d'un concept fondamental de la théorie des probabilités qui décrit le résultat moyen d'une variable aléatoire.
Dans le domaine du trading et de l'investissement, la valeur attendue est utilisée pour calculer le rendement et le risque potentiels d'un investissement ou d'une stratégie de trading.
Mathématiquement, la valeur attendue d'une variable aléatoire est la somme des produits de chaque résultat possible et de sa probabilité.
Par exemple, prenons le cas d'un tirage de pièce de monnaie qui rapporte 1 $ pour les têtes et 0 $ pour les queues.
La valeur attendue de ce tirage au sort est la suivante :
VA = (0.5 * $1) + (0.5 * $0) = $0.50
Cela signifie que le gain moyen pour ce tirage à pile ou face est de 0,50 $. Vous obtiendrez ainsi un seuil de rentabilité au fil du temps, car vos chances correspondent à la probabilité réelle.
En matière de trading et d'investissement, la valeur attendue est utilisée pour estimer les rendements potentiels d'une stratégie de trading ou d'un investissement.
Par exemple, si une action a 60 % de chances d'augmenter sa valeur de 10 % et 40 % de chances de la diminuer de 5 %, le rendement attendu de l'investissement peut être calculé comme suit :
VA = (0.6 * 10%) + (0.4 * -5%) = 6% – 2% = 4%
Cela signifie que le rendement attendu de l'investissement est de 4 %.
Ces informations peuvent aider les investisseurs et les traders à décider d'investir dans l'action, et à évaluer le risque et le rendement potentiel de leur investissement.
La valeur attendue est également importante dans la gestion des risques.
En calculant la valeur attendue d'une stratégie de trading ou d'un investissement, les traders et les investisseurs peuvent évaluer le risque potentiel de l'investissement.
Par exemple, si la valeur attendue d'un investissement est négative, cela signifie que l'investissement est susceptible de perdre de l'argent en moyenne sur le long terme.
Les traders/investisseurs peuvent utiliser ces informations pour gérer leur risque en diversifiant leurs investissements ou en limitant leur exposition à l'investissement ou à la transaction.
En outre, comme nous l'avons également abordé dans d'autres articles, parier sur le résultat à la valeur attendue la plus élevée n'est pas toujours la meilleure décision.
Il est parfois préférable d'avoir une valeur attendue plus faible si cela vous donne une variance plus faible (risque de perte ou d'échec plus faible). En outre, vous voulez toujours vous assurer que vous pouvez couvrir la perte.
Par exemple, si vous disposez de 1 000 $ et que vous avez 90 % de chances de doubler votre argent pour atteindre 2 000 $ et 10 % de chances de perdre la totalité des 1 000 $, votre VA est très élevée (1 800 $ - 1 000 $ = +800 $).
Mais si vous ne pouvez pas vous permettre de perdre les 1 000 $ au cas où vous vous tromperiez, il est préférable de ne pas prendre la décision.
Chaîne de Markov
La chaîne de Markov est un concept mathématique de la théorie des probabilités qui décrit un processus dans lequel l'étape ou l'état suivant dépend uniquement de l'état actuel et non des états précédents.
En d'autres termes, il s'agit d'un processus sans mémoire qui ne s'appuie que sur son état actuel pour déterminer son état futur.
Une chaîne de Markov est définie par un ensemble d'états et les probabilités de passer d'un état à un autre.
Ces probabilités sont souvent représentées dans une matrice de transition, où chaque élément de la matrice représente la probabilité de passer d'un état à un autre.
La chaîne de Markov est importante dans le domaine du trading/investissement car elle peut être utilisée pour modéliser le comportement des marchés financiers.
Le marché boursier, par exemple, est un système complexe comportant un grand nombre de variables affectant le prix des titres qui le composent.
La chaîne de Markov permet de simplifier le système en se concentrant uniquement sur l'état actuel du marché et les probabilités de passer à d'autres états.
En modélisant le marché boursier comme une chaîne de Markov, les traders et les investisseurs peuvent potentiellement obtenir une perspective supplémentaire en prédisant les mouvements futurs du marché sur la base de l'état actuel du marché.
La chaîne de Markov peut également être utilisée pour aider à calculer diverses mesures telles que les rendements attendus, la volatilité et le risque.
En outre, la chaîne de Markov est utilisée dans diverses techniques de modélisation financière telles que l'évaluation des options, l'optimisation des portefeuilles et la gestion des risques.
Elle permet aux traders/investisseurs de créer et de tester différentes stratégies d'investissement, et de mesurer l'efficacité de ces stratégies dans différentes conditions de marché.
Marche aléatoire
La marche aléatoire est un concept mathématique de la théorie des probabilités qui décrit le mouvement d'un objet de manière aléatoire et imprévisible.
Dans une marche aléatoire, la prochaine position de l'objet est déterminée par un processus aléatoire, tel que le tirage au sort ou le lancer d'un dé.
En finance, un modèle de marche aléatoire est souvent utilisé pour décrire l'évolution du cours des actions dans le temps.
La théorie qui sous-tend ce modèle est que le mouvement des prix des actions est imprévisible et suit un modèle aléatoire.
Cela signifie que le prix d'une action à un moment donné a autant de chances de monter que de descendre, et que l'évolution du prix de l'action dans le temps n'est pas influencée par les prix passés ou d'autres facteurs externes. (Bien entendu, il existe diverses idées et théories sur les tendances, le momentum, etc.)
Le concept de marche aléatoire est utile à connaître dans le domaine du trading et de l'investissement car il suggère qu'il est très difficile de prédire l'évolution des cours des actions.
Cela signifie qu'il est difficile de battre constamment le marché en achetant et en vendant des actions sur la base des mouvements de prix passés ou d'autres informations.
Les investisseurs et les traders peuvent utiliser le concept de marche aléatoire pour étayer leur stratégie d'investissement et prendre des décisions plus éclairées.
Par exemple, ils peuvent choisir d'investir dans un portefeuille diversifié d'actions afin de réduire leur exposition aux mouvements individuels des cours boursiers et de diversifier par actifs, classes d'actifs, pays et devises, et envisager l'utilisation d'une stratégie d'achat et de conservation pour éviter les coûts et les risques des transactions fréquentes.
Processus stochastique
Le processus stochastique est un cadre mathématique utilisé pour modéliser le comportement d'un système qui évolue de manière aléatoire dans le temps.
Il s'agit d'une collection de variables aléatoires indexées par le temps, ce qui signifie que la valeur du processus à tout moment donné est aléatoire.
Les processus stochastiques sont utiles en théorie des probabilités car ils peuvent nous aider à analyser le comportement de phénomènes aléatoires qui évoluent dans le temps.
Ils fournissent un moyen de modéliser et de comprendre le caractère aléatoire de ces phénomènes, qui peut être utilisé pour faire des prédictions et prendre des décisions en fonction des résultats attendus.
Dans le domaine du trading et de l'investissement, les processus stochastiques sont utilisés pour modéliser certains comportements des marchés financiers et des prix des actifs.
Ils permettent d'analyser le caractère aléatoire et la volatilité des données financières, qui peuvent être utilisés pour prendre des décisions sur le moment d'acheter ou de vendre des actifs.
Par exemple, les processus stochastiques peuvent être utilisés pour modéliser le mouvement des prix des actions ou des taux de change, ce qui peut aider les traders et les investisseurs à faire des prédictions sur les mouvements futurs de ces marchés.
Les processus stochastiques sont également utilisés pour développer et tester des stratégies de trading. En simulant le comportement des marchés financiers à l'aide de processus stochastiques, les traders et les investisseurs peuvent tester leurs stratégies de trading et évaluer leurs performances dans différentes conditions de marché.
Probabilité conditionnelle
La probabilité conditionnelle est un concept fondamental de la théorie des probabilités qui fait référence à la probabilité qu'un événement se produise si un autre événement s'est déjà produit. C'est un moyen de mettre à jour nos estimations de probabilité sur la base de nouvelles informations.
Plus formellement, la probabilité conditionnelle d'un événement A étant donné que l'événement B s'est produit est définie comme suit :
P(A | B) = P(A et B) / P(B)
Où :
- P(A et B) est la probabilité que les deux événements A et B se produisent, et
- P(B) est la probabilité que l'événement B se produise.
La probabilité conditionnelle est importante en trading et en investissement car elle nous permet de mettre à jour nos estimations de probabilité à mesure que de nouvelles informations deviennent disponibles.
Par exemple, si nous savons qu'une entreprise vient d'annoncer un rapport positif sur ses bénéfices, la probabilité conditionnelle que le cours de l'action augmente compte tenu de cette information est plus élevée qu'avant l'annonce.
Les investisseurs et les traders utilisent la probabilité conditionnelle pour prendre des décisions mieux informées sur la base de nouvelles informations.
En actualisant leurs estimations de probabilité, ils peuvent mieux évaluer les risques et les bénéfices potentiels d'un investissement donné.
Cela peut les aider à réaliser des transactions plus rentables et à gérer leurs risques plus efficacement.
Par exemple, supposons qu'un investisseur envisage d'acheter une action qui a toujours été volatile.
En utilisant la probabilité conditionnelle, l'investisseur peut évaluer la probabilité que le cours de l'action augmente ou diminue en fonction de diverses conditions de marché, telles que des changements dans les taux d'intérêt, la croissance, l'inflation, la politique ou les événements géopolitiques.
Ces informations peuvent aider l'investisseur à prendre une décision plus éclairée quant à l'achat, la conservation ou la vente de l'action.
Loi des grands nombres
La loi des grands nombres est un concept fondamental de la théorie des probabilités qui décrit le comportement de la moyenne d'un grand nombre de variables aléatoires indépendantes.
Cette loi stipule qu'à mesure que le nombre d'essais indépendants augmente, la moyenne de ces essais converge vers la valeur attendue de la distribution de probabilité sous-jacente.
En termes plus simples, la loi des grands nombres stipule que plus une expérience est répétée, plus les résultats observés seront proches du résultat attendu.
Exemple de pile ou face
Par exemple, si l'on tire à pile ou face à plusieurs reprises, la loi des grands nombres prédit que la fréquence des têtes se rapprochera de 50 % à mesure que le nombre de tirages augmentera.
Sur 1 000 essais, il est extrêmement improbable qu'une pièce de monnaie équitable obtienne 55/45 dans un sens ou dans l'autre (0,17 %), mais c'est tout à fait possible sur 100 lancers (36,8 %).
Pourquoi c'est utile
La loi des grands nombres est utile en matière de trading et d'investissement car elle permet d'atténuer le risque lié aux fluctuations imprévisibles du marché.
En investissant dans un portefeuille diversifié, un investisseur peut répartir son risque sur un grand nombre d'actifs, ce qui peut contribuer à réduire l'impact des mouvements de prix des actifs individuels.
En outre, la loi des grands nombres est utile pour analyser les données historiques du marché afin de prendre des décisions d'investissement éclairées.
En examinant un grand nombre de tendances historiques du marché, les investisseurs peuvent aider à identifier des modèles et des tendances qui peuvent les aider à prendre des décisions d'investissement plus éclairées.
Par exemple, si un trader veut savoir si la Réserve fédérale a déjà réduit les taux d'intérêt malgré une inflation supérieure à son objectif, il peut se tourner vers l'histoire pour voir s'il existe des précédents et l'effet que cela a eu sur divers marchés d'actifs.
S'il existe un échantillon, quelle est sa taille pour obtenir suffisamment de données utiles afin de déterminer des conclusions utiles ?
Comment la loi des grands nombres est-elle liée à la signification statistique ?
La loi des grands nombres et la signification statistique sont des concepts liés en statistique, mais ils ne sont pas identiques.
La loi des grands nombres fait référence au fait que la moyenne de l'échantillon d'un grand nombre d'observations indépendantes converge vers la valeur attendue de la distribution de probabilité sous-jacente, lorsque le nombre d'observations approche de l'infini.
La signification statistique, quant à elle, est une mesure de la probabilité que les résultats observés d'une étude ne soient pas dus au hasard.
Dans les tests d'hypothèses statistiques, un résultat est considéré comme statistiquement significatif si la probabilité d'obtenir le résultat observé par hasard est inférieure à un seuil prédéfini, généralement 5 % ou moins.
Dans la pratique, la loi des grands nombres peut être utilisée pour étayer la signification statistique.
Lorsqu'un grand échantillon est collecté et que la moyenne de l'échantillon est proche de la valeur attendue de la distribution sous-jacente, cela suggère que les résultats observés sont moins susceptibles d'être dus au hasard et plus susceptibles d'être statistiquement significatifs.
Cependant, il est important de noter que la signification statistique n'implique pas nécessairement une signification pratique ou une pertinence économique, et que la signification statistique seule ne doit pas être utilisée pour prendre des décisions importantes.
Pour prendre des décisions éclairées, il est essentiel de bien comprendre les données sous-jacentes, les méthodes statistiques et le contexte du problème étudié.
Théorème de Bayes
Le théorème de Bayes est un concept fondamental de la théorie des probabilités qui décrit comment mettre à jour les probabilités en fonction de nouvelles preuves ou informations.
Il doit son nom au révérend Thomas Bayes, un statisticien et théologien britannique du XVIIIe siècle.
Le théorème fournit un moyen de calculer la probabilité d'une hypothèse ou d'un événement sur la base de connaissances ou de croyances antérieures (appelées probabilité antérieure) et de nouvelles preuves (appelées vraisemblance).
La probabilité actualisée est appelée probabilité postérieure, et elle représente la probabilité de l'hypothèse ou de l'événement après prise en compte des nouvelles preuves.
La formule du théorème de Bayes est la suivante :
P(A|B) = P(B|A) * P(A) / P(B)
Où :
- P(A|B) est la probabilité postérieure de l'événement A étant donné la preuve B
- P(B|A) est la probabilité de la preuve B étant donné l'événement A
- P(A) est la probabilité antérieure de l'événement A, et
- P(B) est la probabilité de la preuve B
Le théorème de Bayes est utile dans le domaine du trading et de l'investissement car il peut aider les investisseurs à mettre à jour leurs croyances sur la probabilité de différents événements en fonction de nouvelles informations, telles que des nouvelles sur les bénéfices d'une entreprise ou des indicateurs économiques.
Et c'est là un aspect essentiel de la probabilité bayésienne : elle met à jour vos croyances préalables, sans nécessairement les déterminer ou les recalculer à partir de zéro.
En utilisant le théorème de Bayes, les investisseurs peuvent actualiser leurs probabilités et prendre des décisions d'investissement plus éclairées.
Exemples de l'importance de la vérification de nos hypothèses
Guichetier de banque
Un exemple célèbre du théorème de Bayes en action provient de l'étude de Kahneman et Tversky.
Dans cette étude, les participants ont reçu les informations suivantes :
Linda a 31 ans, elle est célibataire, a un franc-parler et est très intelligente. Elle a étudié la philosophie. Lorsqu'elle était étudiante, elle était très préoccupée par les questions de discrimination et de justice sociale, et a également participé à des manifestations antinucléaires.
Les participants ont ensuite été invités à classer la probabilité de deux scénarios possibles :
- Linda est caissière de banque.
- Linda est caissière de banque et est active dans le mouvement féministe.
Malgré le fait que le premier scénario inclut plus de personnes (tous les guichetiers) que le second (guichetier et féministe), de nombreux participants ont classé le second scénario comme plus probable.
Cela s'explique par le fait que la description de Linda correspond à leur stéréotype de féministe, même si la probabilité que les deux événements se produisent est plus faible que la probabilité du premier événement.
Cet exemple démontre l'importance de vérifier nos hypothèses et de prendre en compte toutes les informations disponibles avant de prendre des décisions.
Le théorème de Bayes peut aider les investisseurs à mettre à jour leurs probabilités et à éviter les biais qui peuvent conduire à des décisions incorrectes.
Steve est-il agriculteur ou bibliothécaire ?
La célèbre étude menée par Kahneman et Tversky portait sur un autre scénario dans lequel les participants devaient déterminer la probabilité que Steve soit soit agriculteur ou bibliothécaire, sur la base d'informations limitées sur sa personnalité.
Les participants ont reçu les informations suivantes :
Steve est un individu calme et timide qui aime lire des livres et n'est pas très sociable.
Sur la base de cette seule information, la plupart des participants ont conclu que Steve avait plus de chances d'être bibliothécaire que fermier. Cependant, Kahneman et Tversky ont montré que cette conclusion n'était pas nécessairement justifiée.
Pour le démontrer, ils ont présenté aux participants des informations supplémentaires pertinentes mais non incluses dans la description initiale.
Par exemple, ils ont ajouté des informations sur le nombre d'agriculteurs par rapport aux bibliothécaires et sur le pourcentage d'agriculteurs ayant le type de personnalité de Steve, ce qui a quand même donné un nombre d'agriculteurs plus élevé que le nombre total de bibliothécaires.
Par exemple, s'il y a 20x plus d'agriculteurs que de bibliothécaires et que 20% des agriculteurs correspondent à ce type de personnalité, il est toujours 4x (20 * 0,20) plus probable que Steve soit un agriculteur qu'un bibliothécaire.
Lorsque les participants ont reçu cette nouvelle information, leurs probabilités que Steve soit un agriculteur ont augmenté de manière significative, ce qui indique que leurs conclusions initiales n'étaient pas suffisamment éclairées.
Cette étude souligne l'importance de mettre à l'épreuve les hypothèses lors de la prise de décisions basées sur des informations limitées.
Il est important de prendre en compte tous les facteurs pertinents et de ne pas se fier uniquement aux hypothèses initiales ou aux heuristiques, telles que les stéréotypes, lors de la prise de décisions ou de la formation de jugements.
Cette approche est conforme à l'approche bayésienne des probabilités, qui implique une mise à jour continue des croyances en fonction des nouvelles informations.
Dans le trading et l'investissement, il est toujours important de se demander comment savez-vous que vous savez ?
Corrélation et covariance
La corrélation et la covariance sont deux concepts statistiques couramment utilisés dans la théorie des probabilités pour décrire la relation entre deux variables aléatoires.
La covariance mesure dans quelle mesure deux variables aléatoires évoluent ensemble, tandis que la corrélation mesure la force et la direction de leur relation.
Une covariance positive indique que les deux variables ont tendance à évoluer dans la même direction, tandis qu'une covariance négative indique qu'elles ont tendance à évoluer dans des directions opposées.
Un coefficient de corrélation va de -1 à 1, les valeurs de 1 indiquant une corrélation positive parfaite, les valeurs de -1 indiquant une corrélation négative parfaite, et les valeurs de 0 indiquant une absence de corrélation.
Dans le domaine du trading/investissement, la corrélation et la covariance sont des outils utiles pour la gestion du risque et la diversification du portefeuille.
En comprenant la relation entre différents actifs, les investisseurs peuvent mieux gérer leurs portefeuilles en sélectionnant des actifs qui ne sont pas fortement corrélés entre eux.
Cela peut contribuer à réduire le risque global du portefeuille en répartissant les investissements entre différentes classes d'actifs et différents secteurs.
Par exemple, un portefeuille d'actions fortement corrélées entre elles peut être plus risqué qu'un portefeuille d'actions ou d'autres actifs faiblement corrélés entre eux.
En sélectionnant une gamme diversifiée d'actifs à faible corrélation, un investisseur peut créer un portefeuille plus résilient, moins susceptible de subir des pertes importantes en cas de baisse du marché.
En outre, la compréhension de la corrélation et de la covariance peut aider les investisseurs à identifier des modèles sur le marché et à prédire les tendances futures.
Il est également important de comprendre que les corrélations sont rétrospectives et ont tendance à évoluer dans le temps.
Par exemple, les actions et les obligations peuvent être négativement corrélées dans un environnement où les changements de l'inflation actualisée diminuent, mais peuvent être positivement corrélées dans des environnements où l'inflation actualisée augmente.
Ainsi, des interprétations plus robustes de l'inflation examineront de plus près l'état intrinsèque des actifs sur la base des liens économiques de cause à effet, plutôt que des interprétations rétrospectives comme les simples coefficients de corrélation, qui ne sont que des sous-produits fugaces de l'environnement dans lequel ils se trouvent.
Brokers de CFD
FAQs - La théorie des probabilités dans le trading
Qu'est-ce que la théorie des probabilités et pourquoi est-elle importante dans le trading ?
La théorie des probabilités est une branche des mathématiques qui traite de l'analyse des phénomènes aléatoires.
Elle fournit un cadre permettant de comprendre la probabilité des événements et le comportement des systèmes qui présentent un caractère aléatoire.
La théorie des probabilités est un outil essentiel pour prendre des décisions éclairées dans des situations où l'issue est incertaine.
Dans le domaine du trading, la théorie des probabilités est cruciale pour comprendre les risques et les rendements potentiels des différentes stratégies d'investissement.
Les traders utilisent la théorie des probabilités pour évaluer la probabilité que certains événements se produisent, comme la probabilité qu'une action prenne de la valeur ou qu'un événement important se produise.
Ils l'utilisent également pour calculer la valeur attendue de leurs transactions, c'est-à-dire le profit ou la perte moyenne qu'ils peuvent s'attendre à réaliser sur le long terme.
En utilisant la théorie des probabilités, les traders peuvent prendre des décisions plus éclairées sur le moment d'entrer ou de sortir d'une transaction, sur le montant à investir et sur la manière de gérer le risque.
Ils peuvent également l'utiliser pour développer et tester des stratégies de trading afin de voir comment elles se comportent dans différentes conditions de marché.
Quels sont les concepts de probabilité les plus importants à comprendre pour les traders ?
Il existe plusieurs concepts de probabilité importants que les traders doivent comprendre.
En voici quelques-uns :
- Distributions de probabilités : Les distributions de probabilités décrivent la probabilité de différents résultats dans un événement aléatoire. Les traders utilisent les distributions de probabilité pour comprendre l'éventail potentiel de résultats pour une transaction donnée. Les distributions de probabilités couramment utilisées en trading comprennent la distribution normale, qui décrit le comportement de nombreuses variables financières, et la distribution binomiale, qui est utilisée pour modéliser les résultats binaires.
- Valeur attendue : La valeur attendue d'une transaction est le profit ou la perte moyenne que l'on peut espérer sur le long terme. En calculant la valeur attendue, les traders peuvent évaluer la rentabilité potentielle d'une transaction et prendre des décisions plus éclairées quant à l'entrée ou la sortie de la transaction.
- Écart type : L'écart-type est une mesure de la quantité de variation ou de volatilité dans un ensemble de données. Les traders utilisent l'écart-type pour comprendre le niveau de risque associé à une transaction donnée. Des niveaux plus élevés d'écart-type indiquent des niveaux de risque plus élevés. Notez que l'écart-type est basé sur la distribution normale, qui ne correspond pas à de nombreux résultats d'actifs financiers/variables.
- Corrélation : La corrélation mesure la force et la direction de la relation entre deux variables. Dans le trading, les traders utilisent la corrélation pour comprendre comment différents actifs évoluent les uns par rapport aux autres. Une corrélation positive élevée entre deux actifs indique qu'ils ont tendance à évoluer dans la même direction, tandis qu'une corrélation négative indique qu'ils ont tendance à évoluer dans des directions opposées.
- Signification statistique : La signification statistique fait référence à la probabilité qu'un résultat observé ne soit pas dû au hasard. Les traders utilisent la signification statistique pour évaluer l'efficacité d'une stratégie de trading ou pour déterminer si un événement particulier est susceptible d'avoir un impact significatif sur le marché.
La compréhension de ces concepts et d'autres concepts de probabilité peut aider les traders à prendre de meilleures décisions sur les marchés et à gérer leurs risques plus efficacement.
Conclusion - La théorie des probabilités dans le trading
La théorie des probabilités joue un rôle crucial dans le trading, car elle aide les traders à prendre des décisions éclairées sur la base d'une analyse fondée sur des données.
En utilisant la théorie des probabilités, les traders peuvent estimer la probabilité des mouvements potentiels du marché et développer des stratégies de trading pour capitaliser sur ces mouvements.
Elle aide les traders à évaluer le rapport risque-récompense d'une transaction, à gérer leur portefeuille et à optimiser leurs positions.
La théorie des probabilités est particulièrement utile pour quantifier l'incertitude et mesurer la volatilité du marché, permettant aux traders d'anticiper et de se préparer aux changements du marché.
Dans l'ensemble, la théorie des probabilités fournit aux traders les outils nécessaires pour prendre des décisions de trading plus informées et plus précises, ce qui peut conduire à une meilleure rentabilité et à une réduction des risques.


