#1 25-12-2023 19:22:09

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 232

Méthodes bayésiennes en finance

L'analyse bayésienne en finance, en trading et en investissement est un cadre qui intègre la modélisation probabiliste et la prise de décision en situation d'incertitude.

Cette approche est basée sur l'inférence bayésienne, où les croyances antérieures sont mises à jour avec de nouvelles informations pour former des croyances postérieures.

Les méthodes bayésiennes en finance offrent un cadre probabiliste permettant d'incorporer des connaissances préalables et des données en temps réel pour modéliser l'incertitude et prendre des décisions éclairées.

Les applications comprennent la gestion des risques, l'optimisation des portefeuilles et l'évaluation des actifs.

Les méthodes bayésiennes non paramétriques sont capables de capturer des modèles et des relations complexes dans les données sans être limitées par les structures rigides des modèles paramétriques.

Leur adaptabilité et leur capacité à intégrer des connaissances préalables les rendent particulièrement adaptées aux marchés financiers.

Les méthodes bayésiennes variationnelles en finance permettent l'application de modèles bayésiens à des problèmes complexes et de haute dimension pour lesquels les méthodes traditionnelles peuvent être prohibitives sur le plan informatique.

En fournissant une inférence plus rapide et évolutive, elles sont particulièrement utiles dans les domaines nécessitant une analyse en temps réel ou le traitement de données financières à grande échelle.

Concepts clés de l'analyse bayésienne en finance

Explorons les concepts clés :

Inférence bayésienne

Il s'agit du processus de mise à jour de l'estimation de la probabilité d'une hypothèse au fur et à mesure que de nouvelles preuves ou informations sont disponibles.

Il s'agit d'un élément central de l'analyse bayésienne en finance, où les informations du marché sont continuellement incorporées dans les modèles.

Un exemple courant serait l'intégration d'informations provenant d'une annonce de résultats dans le prix d'une action.

Les résultats actualisent une vision existante d'une entreprise, de ses finances, de son orientation et de ce que cela signifie pour ses actions.

Probabilité bayésienne

Contrairement à la probabilité fréquentiste, qui interprète la probabilité comme la fréquence à long terme des événements, la probabilité bayésienne est une mesure du degré de croyance ou de confiance dans l'occurrence d'un événement.

Théorème de Bayes

Ce théorème décrit comment mettre à jour les probabilités des hypothèses lorsqu'on dispose de preuves.

Il est fondamental dans l'analyse bayésienne pour réviser les croyances à la lumière de nouvelles données.

Théorème de Bernstein-von Mises

Ce théorème justifie les méthodes bayésiennes d'un point de vue fréquentiste, en montrant que, sous certaines conditions, la distribution postérieure bayésienne converge vers une distribution normale centrée sur la vraie valeur du paramètre à mesure que la taille de l'échantillon augmente.

Cohérence

Dans l'analyse bayésienne, la cohérence fait référence à la consistance interne d'un ensemble de probabilités.

Un ensemble cohérent de probabilités ne contient pas de contradictions.

Théorème de Cox

Ce théorème sous-tend les fondements de la théorie bayésienne des probabilités, en montrant que l'actualisation bayésienne découle logiquement de certains axiomes de cohérence.

En finance, par exemple, une action réagit de manière prévisible à l'annonce d'un bénéfice en fonction de l'évolution des résultats par rapport aux attentes actualisées.

Règle de Cromwell

Dans l'analyse bayésienne, cette règle conseille de ne pas attribuer une probabilité de 0 ou de 1 à un événement à moins qu'il ne soit logiquement certain.

Elle reconnaît la nécessité de garder l'esprit ouvert à de nouvelles preuves.

L'un des problèmes des traders est qu'ils deviennent souvent trop confiants alors que les marchés sont en fin de compte un jeu de probabilités.

C'est pourquoi les résultats futurs des actifs que l'on négocie sont généralement représentés de manière analytique sous la forme de distributions, telles que les suivantes :

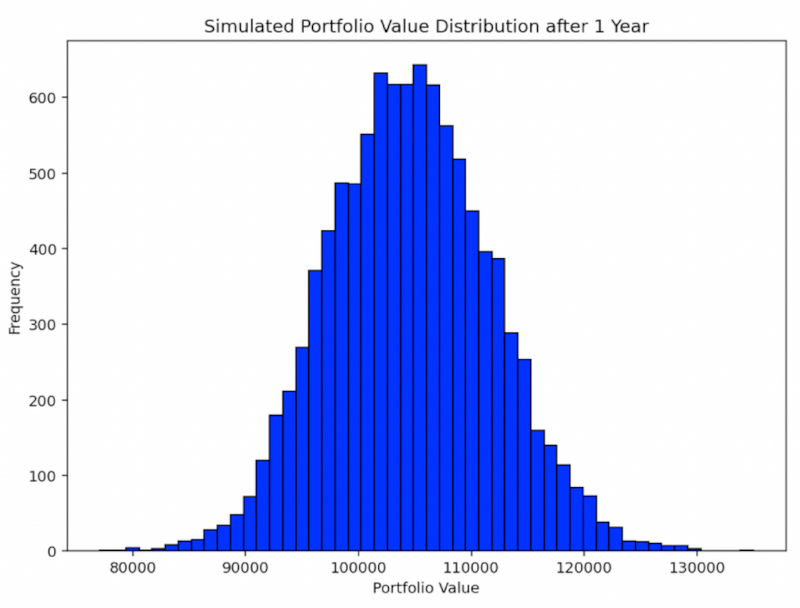
En rapport : Biais psychologiques et comment les éviter

Principe d'indifférence

Ce principe suggère d'attribuer des probabilités égales à tous les résultats lorsqu'aucune information supplémentaire n'est disponible.

Par exemple, si vous avez le choix entre l'action A et l'action B et que vous n'avez étudié aucune des deux sociétés, il n'est probablement pas judicieux de parier sur l'une plutôt que sur l'autre.

Principe de l'entropie maximale

Lors du choix d'une distribution de probabilité, il convient de choisir la distribution ayant l'entropie maximale compatible avec les contraintes données, afin d'obtenir l'estimation la moins biaisée possible.

Construction de modèles

En finance, la construction d'un modèle bayésien implique la spécification d'une distribution a priori et d'une fonction de vraisemblance, à partir desquelles la distribution a posteriori est dérivée.

A priori faible ... A priori fort

• Un a priori faible (ou non informatif) reflète un manque de connaissances préalables.

• Un a priori fort est basé sur des connaissances préalables substantielles ou des croyances fortes sur les paramètres.

A priori conjugué

Un a priori conjugué est choisi parce que sa forme simplifie le calcul analytique de la distribution a posteriori.

Régression linéaire

La régression linéaire bayésienne utilise le théorème de Bayes pour l'analyse de régression, fournissant des interprétations probabilistes des paramètres du modèle et des prédictions.

Bayes empirique

Cette méthode estime les distributions préalables à partir des données.

Elle combine les idées des statistiques fréquentistes et bayésiennes.

Modèle hiérarchique

Cette méthode consiste à structurer les paramètres en couches, chaque couche étant conditionnée par les paramètres de la couche supérieure. Elle est utile pour traiter les structures de données complexes en finance.

Exemple de modèle hiérarchique en finance

Dans un modèle bayésien hiérarchique appliqué à la finance, on peut structurer le modèle de manière à ce que les rendements des actifs individuels soient conditionnés par des paramètres spécifiques au secteur, qui sont à leur tour conditionnés par des paramètres de marché plus larges.

Par exemple, si le S&P 500 augmente de 1 % en une journée en raison d'une certaine baisse des taux d'intérêt, on peut supposer que le secteur de l'énergie se comportera de la même manière.

Cela permet une analyse nuancée qui saisit à la fois les comportements des actifs au niveau microéconomique et les tendances du marché au niveau macroéconomique.

Cette approche stratifiée facilite la modélisation des dépendances et des interactions complexes au sein des ensembles de données financières.

Elle permet une compréhension plus détaillée et interconnectée des dynamiques de risque et de rendement à différents niveaux d'un marché financier donné.

Approximation postérieure

Des techniques telles que la chaîne de Markov Monte Carlo (MCMC), l'approximation de Laplace, les approximations de Laplace intégrées et imbriquées, et l'inférence variationnelle sont utilisées pour l'approximation de distributions postérieures complexes qui sont difficiles à calculer analytiquement.

Chaîne de Markov Monte Carlo (MCMC)

Technique de calcul qui utilise l'échantillonnage aléatoire pour approximer des distributions postérieures complexes et de haute dimension dans l'inférence bayésienne.

Approximation de Laplace

Méthode qui approxime une distribution postérieure complexe par une distribution gaussienne centrée sur le mode de la distribution postérieure.

Approximations de Laplace intégrées et imbriquées (ALII)

Technique d'inférence bayésienne approximative dans les modèles gaussiens latents, offrant des calculs plus rapides que le MCMC.

Inférence variationnelle

Approche basée sur l'optimisation qui approxime les distributions postérieures complexes par des distributions paramétrées plus simples afin de rendre l'inférence bayésienne calculable.

Estimateurs

Dans l'analyse bayésienne, les estimateurs sont utilisés pour résumer la distribution a posteriori, comme l'estimateur bayésien et l'estimation maximale a posteriori.

Intervalle crédible

Il s'agit de l'équivalent bayésien des intervalles de confiance, représentant l'intervalle dans lequel un paramètre non observé se situe avec une certaine probabilité.

Approximation de la preuve et limite inférieure de la preuve

Il s'agit de méthodes utilisées dans la sélection de modèles bayésiens et pour l'approximation des preuves en faveur d'un modèle.

Échantillonnage imbriqué

Technique utilisée pour le calcul bayésien, en particulier pour le calcul des preuves d'un modèle.

Évaluation du modèle

Dans l'analyse bayésienne, l'évaluation du modèle est essentielle.

Le facteur de Bayes, le calcul de la moyenne du modèle et les vérifications prédictives postérieures sont des outils permettant d'évaluer l'adéquation et la précision prédictive des modèles bayésiens.

Résumé

Dans les contextes financiers, ces concepts sont importants pour développer des modèles qui s'adaptent aux nouvelles informations, gèrent les risques et font des prédictions.

Les méthodes bayésiennes permettent une approche plus nuancée et plus souple de la modélisation des marchés financiers, en tenant compte de la nature dynamique des données financières.

L'analyse bayésienne offre un cadre permettant d'aborder les inconnues et d'incorporer les croyances subjectives dans la finance.

       

Applications de l'analyse bayésienne

Les applications de l'analyse bayésienne dans la construction de portefeuilles, l'évaluation et la gestion des risques sont considérables.

Construction de portefeuille

Intégration des opinions et des incertitudes

Les méthodes bayésiennes permettent d'intégrer des points de vue subjectifs (d'experts du marché, par exemple) aux données historiques.

Allocation dynamique des actifs

Les techniques bayésiennes permettent une mise à jour dynamique de l'allocation d'actifs au fur et à mesure que de nouvelles données sont disponibles, ce qui facilite l'adaptation aux changements du marché.

Modélisation des rendements

Les modèles bayésiens, tels que la régression bayésienne, peuvent être utilisés pour modéliser les rendements des actifs.

Adaptation aux préférences des investisseurs

Les méthodes bayésiennes permettent d'adapter les portefeuilles aux préférences individuelles en matière de risque et aux horizons d'investissement.

Cela permet de prendre en compte l'incertitude des estimations des rendements et des risques.

L'évaluation

Estimation des flux de trésorerie et des taux d'actualisation

Les modèles bayésiens peuvent fournir une approche probabiliste pour estimer les flux de trésorerie et les taux d'actualisation futurs.

Évaluation des options réelles

L'analyse bayésienne aide à évaluer les options réelles, lorsque la prise de décision est séquentielle et que l'information est révélée au fil du temps.

Fusions et acquisitions

Dans les scénarios de fusions et acquisitions, les méthodes bayésiennes peuvent être utilisées pour incorporer des informations provenant de diverses sources afin d'évaluer les entreprises cibles dans des conditions d'incertitude.

Évaluation des start-ups

Les startups manquent souvent de données historiques. L'analyse bayésienne permet de combiner les données du marché et les avis d'experts pour estimer leur valeur.

Gestion des risques

Modélisation du risque de crédit

Les techniques bayésiennes permettent d'incorporer des connaissances préalables et des avis d'experts dans les modèles de risque de crédit, ce qui est particulièrement utile lorsque les données historiques sont rares ou non représentatives.

Évaluation du risque de marché

Dans le domaine du risque de marché, les méthodes bayésiennes permettent de mettre à jour de manière dynamique la distribution des rendements des actifs, ce qui conduit à des calculs plus précis de la valeur à risque (VaR) ou de l'espérance de perte (EP).

Risque opérationnel

Pour le risque opérationnel, qui manque souvent de données historiques suffisantes, les approches bayésiennes peuvent combiner des données internes, des données externes et le jugement d'experts.

Tests de résistance et analyse de scénarios

Les modèles bayésiens peuvent être utilisés pour générer et mettre à jour des scénarios de simulation de crise, en tenant compte des conditions actuelles du marché et des informations prospectives.

Risque de liquidité

Les réseaux bayésiens peuvent modéliser les dépendances entre divers facteurs de marché et le risque de liquidité, ce qui permet de mieux comprendre la probabilité de crises de liquidité dans différents scénarios.

Résumé de l'étude

Dans chacun de ces domaines, l'analyse bayésienne améliore les méthodes traditionnelles en intégrant un niveau de raisonnement probabiliste et en traitant les inconnues de manière plus explicite.

Elle permet aux analystes financiers et aux décideurs de quantifier leur confiance dans diverses hypothèses et résultats.

Méthodes bayésiennes variationnelles en finance

Les méthodes bayésiennes variationnelles constituent une alternative aux techniques traditionnelles comme la chaîne de Markov Monte Carlo (MCMC) pour l'approximation des distributions postérieures dans l'inférence bayésienne - utile en finance où les modèles impliquent souvent des données complexes et de haute dimension.

Ces méthodes transforment le problème de l'inférence bayésienne en un problème d'optimisation. Cela permet d'obtenir une efficacité de calcul et une évolutivité.

Concepts et techniques clés

Inférence variationnelle (IV)

IV approxime la distribution postérieure par une distribution plus simple.

Il optimise les paramètres de cette distribution plus simple pour qu'elle soit aussi proche que possible de la vraie distribution postérieure.

Approximation du champ moyen

Approche courante en IV où la distribution conjointe est approximée par un produit de distributions indépendantes, ce qui simplifie les calculs.

Limite inférieure de preuve (LIPR)

Dans l'inférence variationnelle stochastique, l'optimisation consiste à maximiser l'LIPR, qui est une limite inférieure de l'évidence du modèle (ou de la vraisemblance marginale).

Inférence variationnelle stochastique (IVS)

Le IVS associe le IV à l'optimisation stochastique.

Il est ainsi possible de traiter les grands ensembles de données que l'on rencontre souvent en finance.

Applications en finance

Gestion du risque

Les méthodes variationnelles permettent d'estimer efficacement les distributions postérieures des modèles de risque, tels que les modèles de valeur à risque (VaR), en particulier lorsqu'il s'agit de grands portefeuilles ou de dynamiques d'actifs complexes.

Optimisation de portefeuille

Dans l'optimisation bayésienne de portefeuille, les méthodes variationnelles peuvent traiter des modèles complexes, tels que ceux qui incorporent les croyances des investisseurs et les opinions du marché, plus efficacement que le modèle MCMC.

Modèles d'évaluation des actifs

L'estimation des paramètres de modèles sophistiqués d'évaluation d'actifs - en particulier ceux qui comportent un grand nombre de variables latentes ou de facteurs - peut être plus efficace en termes de calcul grâce aux méthodes variationnelles.

Trading algorithmique

Pour les stratégies de trading à haute fréquence, où la vitesse est le facteur principal, les méthodes variationnelles offrent une inférence plus rapide que les méthodes bayésiennes traditionnelles.

Cela permet une mise à jour en temps réel des modèles de trading.

Modélisation du risque de crédit

Dans la modélisation du risque de crédit, en particulier avec de grands portefeuilles ou des structures de corrélation complexes, les méthodes bayésiennes variationnelles fournissent une solution évolutive pour l'estimation des probabilités de défaut et des distributions de pertes.

Prévisions macroéconomiques

Les méthodes bayésiennes variationnelles sont utilisées dans les modèles d'équilibre général stochastique dynamique (EGSD) et d'autres modèles macroéconomiques complexes pour une inférence et une prédiction plus rapides.

Analyse des séries temporelles

Les méthodes variationnelles conviennent à l'analyse bayésienne des séries temporelles, y compris les modèles espace-état et les modèles linéaires dynamiques.

Permet des mises à jour et des prévisions plus rapides.

Réseaux neuronaux bayésiens

En appliquant les réseaux neuronaux à la modélisation financière, les méthodes bayésiennes variationnelles offrent un moyen de quantifier l'incertitude dans les prédictions.

Résumé

Les méthodes bayésiennes variationnelles en finance permettent l'application de modèles bayésiens à des problèmes complexes et de haute dimension pour lesquels les méthodes traditionnelles peuvent être prohibitives sur le plan informatique.

En fournissant une inférence plus rapide et évolutive, elles sont particulièrement utiles dans les domaines nécessitant une analyse en temps réel ou le traitement de données financières à grande échelle.

Leur capacité à quantifier les inconnues et à intégrer les connaissances préalables continue à en faire un choix de plus en plus populaire dans diverses applications financières.

Méthodes bayésiennes non paramétriques en finance

Les méthodes bayésiennes non paramétriques en finance sont précieuses pour leur flexibilité dans la modélisation de données financières complexes et dynamiques sans supposer une forme paramétrique spécifique.

Ces méthodes s'adaptent à la structure des données.

Elles sont donc bien adaptées aux caractéristiques souvent non linéaires et non normales/à queue grasse des marchés financiers.

Les principales applications et techniques sont les suivantes :

Techniques clés

Processus de Dirichlet (PD)

Le processus de Dirichlet est une méthode bayésienne non paramétrique couramment utilisée pour regrouper ou modéliser des distributions de mélanges sans spécifier à l'avance le nombre de grappes ou de composants du mélange.

Il est utile en finance pour modéliser les distributions de rendements, identifier les régimes dans les séries chronologiques financières ou regrouper les actifs.

Processus gaussiens (PG)

Les processus gaussiens sont utilisés pour les tâches de régression et de classification, offrant une approche flexible de la modélisation des fonctions inconnues.

En finance, ils sont utilisés pour les prévisions de séries temporelles, la modélisation des courbes de rendement et la gestion des risques.

Régression non paramétrique bayésienne

Cette approche étend les modèles de régression traditionnels en autorisant un nombre infini de paramètres.

Elle est utile pour les relations complexes dans les données financières, telles que la relation entre les variables macroéconomiques et les prix des actifs.

Modèles de Markov cachés infinis (MMCI)

Dans les MMCI, le nombre d'états latents n'est pas fixe, ce qui permet une modélisation plus souple des séries temporelles avec des régimes ou des comportements changeants, tels que le regroupement de la volatilité dans les rendements des actifs.

Applications en finance

Gestion des risques

Les méthodes bayésiennes non paramétriques peuvent modéliser la distribution des rendements ou des pertes d'actifs de manière plus précise, en tenant compte des queues grasses et des asymétries souvent observées sur les marchés financiers.

Évaluation des actifs et répartition des portefeuilles

Ces méthodes permettent une modélisation plus souple de la dynamique des rendements des actifs et des corrélations.

Cela permet de construire des portefeuilles et des modèles d'évaluation des actifs plus robustes.

Trading algorithmique

Dans le cadre du trading algorithmique, les modèles non paramétriques peuvent s'adapter plus efficacement aux nouvelles conditions du marché - en capturant des modèles complexes dans les données à haute fréquence pour les stratégies de trading.

Évaluation du crédit et prévision des défaillances

Les modèles non paramétriques peuvent être utilisés pour modéliser la probabilité de défaillance sans supposer une forme de distribution spécifique, ce qui peut améliorer la précision des modèles de risque de crédit.

Modélisation de la courbe de rendement

Les méthodes non paramétriques permettent une modélisation flexible de la courbe de rendement.

Prévisions macroéconomiques

Ces méthodes permettent de prévoir les indicateurs économiques sans imposer d'hypothèses restrictives sur les relations économiques sous-jacentes.

Modélisation des actifs illiquides

Pour les actifs dont les données sont peu nombreuses, comme certains titres à revenu fixe ou l'immobilier, les modèles bayésiens non paramétriques peuvent tirer parti de leur flexibilité pour fournir de meilleures estimations de la valeur et du risque.

Voir aussi : Modèles non paramétriques en finance

Exemple de codage - Méthodes bayésiennes pour l'optimisation de portefeuille

Pour démontrer un exemple de codage des méthodes bayésiennes dans l'optimisation de portefeuille, nous utiliserons un scénario simplifié.

Nous supposerons un portefeuille composé de quelques actifs et nous utiliserons les rendements historiques pour mettre à jour nos croyances sur les rendements attendus de ces actifs.

Pour des raisons de simplicité, nous utiliserons des données synthétiques.

Le code suivra les étapes suivantes :

• Générer des rendements historiques synthétiques pour quelques actifs.

• Définir une distribution préalable pour les rendements attendus (par exemple, une distribution normale).

• Mettre à jour la distribution avec les données synthétiques en utilisant l'inférence bayésienne.

• Optimiser le portefeuille sur la base des croyances actualisées concernant les rendements attendus.

Nous utiliserons des bibliothèques Python telles que numpy pour les opérations numériques et scipy pour les fonctions statistiques.

import numpy as np
from scipy.stats import norm
import scipy.optimize as optimize

# Générer des rendements historiques synthétiques pour 3 actifs
np.random.seed(0)
n_assets = 3
n_obs = 1000
historical_returns = np.random.randn(n_obs, n_assets) * 0.05

# Définir des priorités pour les rendements attendus (moyenne 0, std 0,1)
priors = [norm(loc=0, scale=0.1) for _ in range(n_assets)]

# Mise à jour des croyances avec les données historiques (estimation a posteriori)
# En supposant un a priori conjugué, nous mettons à jour la moyenne (exemple simple)
posterior_means = [(prior.mean() + historical_returns[:,i].mean()) / 2 for i, prior in enumerate(priors)]
posterior_stds = [0.05 for _ in range(n_assets)] # Simplified standard deviation

# Définir la fonction objective pour l'optimisation du portefeuille (maximiser le rendement attendu)
def portfolio_expected_return(weights):
return -np.dot(posterior_means, weights)

# Contraintes : la somme des poids est égale à 1 et est limitée entre 0 et 1
constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
bounds = tuple((0, 1) for _ in range(n_assets))

# Estimation initiale (répartition égale)
init_guess = [1/n_assets] * n_assets

# Optimisation du portefeuille
optimized_weights = optimize.minimize(portfolio_expected_return, init_guess, method='SLSQP', bounds=bounds, constraints=constraints)

optimized_weights.x # Optimized portfolio weights based on Bayesian updated beliefs

Dans cet exemple Python, nous avons généré des rendements historiques synthétiques pour trois actifs et utilisé un mécanisme simple de mise à jour bayésienne pour estimer les rendements attendus postérieurs.

La distribution préalable du rendement attendu de chaque actif a été supposée être une distribution normale avec une moyenne de 0 et un écart type de 0,1.

Les moyennes postérieures ont été estimées en faisant la moyenne de la moyenne antérieure et de la moyenne de l'échantillon des données synthétiques.

Pour l'optimisation du portefeuille, l'objectif était de maximiser le rendement attendu, qui est la valeur négative du produit de points des moyennes postérieures et des pondérations du portefeuille.

L'optimisation a été soumise aux contraintes suivantes : la somme de tous les poids est égale à 1 et chaque poids est compris entre 0 et 1.

Le résultat de l'optimisation suggère une répartition égale entre les trois actifs, ce qui est le résultat des hypothèses simplistes et des données synthétiques utilisées.

Méthodes bayésiennes en finance, exemple de codage en Python

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.