Vous n'êtes pas identifié(e).
- Contributions: Récentes | Sans réponse
#1 27-01-2024 19:51:55
- Climax
- Administrateur

- Inscription: 30-08-2008
- Messages: 6 411


La géométrie différentielle en finance, trading et marchés
La géométrie différentielle est un domaine des mathématiques qui traite des formes lisses et des propriétés des surfaces et des courbes.
Elle trouve des applications dans les marchés financiers et le trading, principalement dans la gestion des risques, l'optimisation des portefeuilles et les modèles d'évaluation des options.
Sa valeur dans ces domaines découle de sa capacité à modéliser et à analyser des relations complexes, multidimensionnelles et non linéaires (tout en apportant un élément visuel).
Principaux enseignements
La géométrie différentielle est un domaine des mathématiques qui utilise le calcul et l'algèbre pour étudier la géométrie des courbes et des surfaces. Elle peut être utile aux traders quantitatifs.
Comprendre la dynamique des marchés à l'aide des formes
La compréhension de la courbure et de la topologie des manifolds représentant des données financières peut aider les traders à identifier des modèles ou des relations inconnus entre les actifs.
Gestion des risques et optimisation des portefeuilles
La géométrie différentielle peut aider à optimiser les portefeuilles dans un espace courbe, qui reflète mieux les marchés financiers réels que l'espace plat supposé dans les modèles linéaires traditionnels.
Cette approche prend en compte les non-linéarités et les complexités des marchés et des données financières.
Stratégies avancées de tarification et de couverture des produits dérivés
La géométrie différentielle permet de modéliser et de comprendre des instruments financiers complexes (en particulier les produits dérivés).
L'approche géométrique permet de mieux comprendre leur comportement dans diverses conditions de marché.
Cela peut aider à développer des modèles de tarification et des stratégies de couverture efficaces, principalement pour les options et autres instruments dont les valeurs dépendent de multiples variables sous-jacentes.
Concepts de géométrie différentielle en finance
La géométrie différentielle, à la base, implique l'étude de formes lisses et de la vitesse à laquelle les quantités changent.
En finance, cette discipline mathématique peut être appliquée à la courbure et à la topologie du collecteur des portefeuilles de trading/investissement ou des distributions de probabilité.
Cette approche permet de mieux comprendre le profil risque-rendement de différents instruments financiers ou portefeuilles.
Voici quelques concepts clés pour lesquels la géométrie différentielle peut être utilisée en finance :
Courbure et dynamique du marché
En géométrie différentielle, la courbure mesure la façon dont une courbe s'écarte d'une ligne droite ou une surface d'un plan.
En finance, ce concept peut être appliqué pour comprendre la "courbure" (c'est-à-dire la non-linéarité et la multidimensionnalité) des données financières.
Manifolds dans l'optimisation de portefeuille
Les manifolds sont des espaces qui ressemblent localement à l'espace euclidien et peuvent être utilisés pour représenter des instruments financiers ou des portefeuilles complexes.
Dans le cadre de l'optimisation de portefeuille, les manifolds peuvent représenter l'ensemble de toutes les combinaisons de portefeuilles possibles.
Les outils de la géométrie différentielle, comme les espaces tangents et les géodésiques, peuvent aider à trouver le chemin optimal ou la combinaison de portefeuilles qui maximise les rendements pour un niveau de risque donné.
Par exemple, supposons que vous ayez un portefeuille de 5 actifs (tous non corrélés, de même rendement et de même risque) et que vous essayiez de déterminer comment obtenir le rendement le plus élevé pour le niveau de risque que vous prenez.
La géométrie différentielle peut aider à montrer la forme de cet exercice d'optimisation par le biais d'un collecteur.
Dans ce cas, il est plus risqué de tout concentrer dans un seul actif (la partie bleue du collecteur, à l'extrémité où il est le plus raide) et de le répartir entre les cinq actifs pour obtenir le meilleur rapport rendement/risque (la partie jaune et plate de la surface).
Nous avons présenté une courbe 2D de ces données dans un article séparé.
Le mouvement brownien géométrique dans l'évaluation des options
Utilisé notamment dans le modèle de Black-Scholes pour l'évaluation des options,
Le mouvement brownien géométrique est un processus stochastique à temps continu dans lequel le logarithme de la variable suit un mouvement brownien (une marche aléatoire).
La géométrie différentielle permet d'analyser de tels processus stochastiques, qui sont utilisés pour comprendre et prédire les mouvements de prix des produits dérivés.
Mesures du risque et hypersurfaces
Les mesures du risque telles que la valeur à risque (VaR) et la valeur à risque conditionnelle (CVaR) peuvent être représentées comme des hypersurfaces dans un espace multidimensionnel où chaque dimension représente un actif ou un facteur de risque différent.
La géométrie différentielle permet une analyse plus sophistiquée de ces hypersurfaces.
Cela peut aider à comprendre la structure et le comportement des risques dans un portefeuille.
Faisceaux de fibres dans les réseaux financiers
Les faisceaux de fibres, structures composées d'un espace "de base" et de "fibres" à chaque point de l'espace de base, peuvent être utilisés pour modéliser les réseaux financiers.
Chaque nœud (par exemple, une institution financière) est un point de l'espace de base, et les fibres représentent l'état ou le comportement de ce nœud.
Cette approche permet de comprendre le risque systémique et l'interconnexion des entités financières.
Théorie du transport optimal
Ce domaine, qui a ses racines dans la géométrie différentielle, implique l'optimisation du mouvement des ressources (comme les biens ou les marchandises) et est pertinent dans les stratégies de minimisation des coûts.
Elle trouve également des applications dans l'étalonnage des modèles et dans la mesure des distances entre les distributions de probabilité, ce qui est utile dans la gestion des risques.
La topologie différentielle dans le trading algorithmique
Dans le domaine du trading algorithmique, la topologie différentielle peut être appliquée pour analyser la structure des données des marchés financiers et pour concevoir des algorithmes qui s'adaptent à l'évolution des conditions du marché.
L'étude de la topologie des mouvements de prix peut permettre de mieux comprendre le comportement du marché.
Moments et cumuls des distributions de probabilité
Les moments (comme la moyenne, la variance, l'asymétrie, l'aplatissement) sont des mesures quantitatives qui décrivent la forme d'une distribution de probabilité.
Les cumulants, liés aux moments, fournissent un moyen complémentaire de caractériser les distributions, particulièrement utile pour traiter les processus non gaussiens/non normaux courants sur les marchés financiers.
Application à l'optimisation de portefeuille
Dans l'optimisation de portefeuille, le cadre traditionnel de la moyenne-variance peut être amélioré de manière significative en utilisant la géométrie différentielle.
Ce cadre se concentre généralement sur les deux premiers moments (moyenne et variance), mais l'intégration de moments plus élevés (comme l'asymétrie et l'aplatissement) peut conduire à une représentation plus précise de la distribution des rendements d'un portefeuille.
La géométrie différentielle permet d'explorer ces moments à plus haute dimension d'une manière plus facile et plus intuitive.
Interprétation géométrique du risque et du rendement
En considérant l'espace des rendements de portefeuille comme un objet géométrique, on peut utiliser la géométrie différentielle pour comprendre comment de petits changements dans la composition du portefeuille peuvent entraîner des changements dans le profil risque-rendement.
Cela peut impliquer l'étude de la courbure de l'espace, qui est liée à la façon dont le risque (dont la variance fait partie) change lorsqu'on passe d'un portefeuille à un autre.
Modèles et algorithmes avancés
La combinaison de la géométrie différentielle et des processus stochastiques permet de développer des modèles et des algorithmes sophistiqués pour la sélection de portefeuilles.
Ces modèles peuvent saisir plus précisément les complexités des marchés financiers, y compris les relations non linéaires et les risques extrêmes qui sont souvent négligés dans les modèles plus simples.
Implications pratiques
Pour les praticiens, l'application de la géométrie différentielle à l'optimisation des portefeuilles pourrait impliquer l'utilisation d'outils tels que le manifold learning, qui permet de découvrir la géométrie intrinsèque des données financières à haute dimension.
Cela peut conduire à de meilleures techniques de construction de portefeuille qui sont sensibles aux structures géométriques sous-jacentes des données.
Géométrie différentielle et apprentissage automatique en finance
La géométrie différentielle, qui met l'accent sur les courbes, les surfaces et les formes, combinée à l'apprentissage automatique, offre aux traders quantiques un autre cadre d'analyse pour modéliser les relations complexes et non linéaires dans les données financières.
Cette synergie améliore la capacité à découvrir des modèles et des dépendances cachés dans les données du marché, ce qui peut aider à concevoir de meilleures stratégies de trading et un meilleur avantage.
En employant des techniques telles que l'apprentissage multiple, les traders peuvent extraire des informations significatives d'ensembles de données financières à haute dimension.
Géométrie différentielle et géométrie de l'information en finance et sur les marchés
La géométrie différentielle et la géométrie de l'information sont deux disciplines mathématiques similaires qui trouvent des applications dans la finance et les marchés.
Comprendre leurs différences et leurs utilisations spécifiques peut permettre de mieux comprendre la modélisation et l'analyse financières.
La géométrie différentielle en finance et sur les marchés
Courbure et dynamique des marchés
Les concepts de courbure et de forme de la géométrie différentielle permettent d'analyser la courbure dans différentes allocations d'actifs.
Surfaces de risque et optimisation de portefeuille
La géométrie différentielle est utilisée pour visualiser et optimiser des surfaces de risque complexes dans le cadre de la gestion de portefeuille.
Par exemple, la courbure d'une surface de risque peut indiquer la stabilité du portefeuille en cas de tensions sur le marché.
Modélisation d'instruments financiers complexes
La géométrie différentielle est utilisée pour modéliser les structures complexes de divers instruments financiers et comprendre leur comportement dans différentes conditions de marché.
Il peut s'agir d'options exotiques pour lesquelles il existe diverses structures non linéaires ou probabilistes qui peuvent être modélisées géométriquement.
Mouvement brownien géométrique
Ce concept, pierre angulaire du modèle de Black-Scholes pour l'évaluation des options, est une application clé de la géométrie différentielle.
Il modélise les mouvements du cours des actions et contribue à l'évaluation des options.
Géométrie de l'information dans la finance et les marchés
Distributions de probabilités et analyse des données
La géométrie de l'information s'applique à l'étude des distributions de probabilité, en particulier à la compréhension de la structure des données du marché.
Elle se concentre sur la géométrie des modèles statistiques.
Mesure du risque et de l'incertitude
Elle est utilisée pour quantifier l'incertitude dans les modèles financiers.
La divergence entre différentes distributions de probabilité peut être analysée à l'aide de la géométrie de l'information.
Dynamique des prix des actifs
La géométrie de l'information fournit des outils pour comprendre la dynamique des prix des actifs en examinant le manifeste statistique des mouvements de prix et la manière dont il évolue dans le temps.
Modèles de trading algorithmique et de prédiction du marché
En créant des modèles pour le trading algorithmique, la géométrie de l'information aide à analyser les modèles de données et à prédire les tendances futures du marché.
Comparaison et application en finance
Focus
La géométrie différentielle se concentre sur les aspects structurels, basés sur la forme, des modèles financiers.
La géométrie de l'information traite des propriétés statistiques et des incertitudes au sein de ces modèles.
Complexité et dimensionnalité
La géométrie différentielle traite de la courbure et des formes dans des espaces de dimensions supérieures, ce qui est important pour la modélisation d'instruments financiers complexes.
La géométrie de l'information, quant à elle, traite de la forme des modèles statistiques. Elle se concentre sur les distributions de probabilité sous-jacentes des données du marché.
Approche de la modélisation
La géométrie différentielle fournit un cadre pour comprendre la structure géométrique des modèles financiers.
La géométrie de l'information permet de comprendre l'incertitude et l'information contenues dans ces modèles.
Applications pratiques
La géométrie différentielle s'intéresse davantage à la structure et à la relation entre les différents instruments financiers et les marchés.
La géométrie de l'information permet d'extraire des informations des données du marché, de comprendre la dynamique du marché et de faire des prédictions basées sur des modèles statistiques.
En bref, la géométrie différentielle s'intéresse davantage à la structure géométrique et physique des modèles financiers, tandis que la géométrie de l'information se concentre sur la nature statistique et probabiliste des données et des modèles de marché.
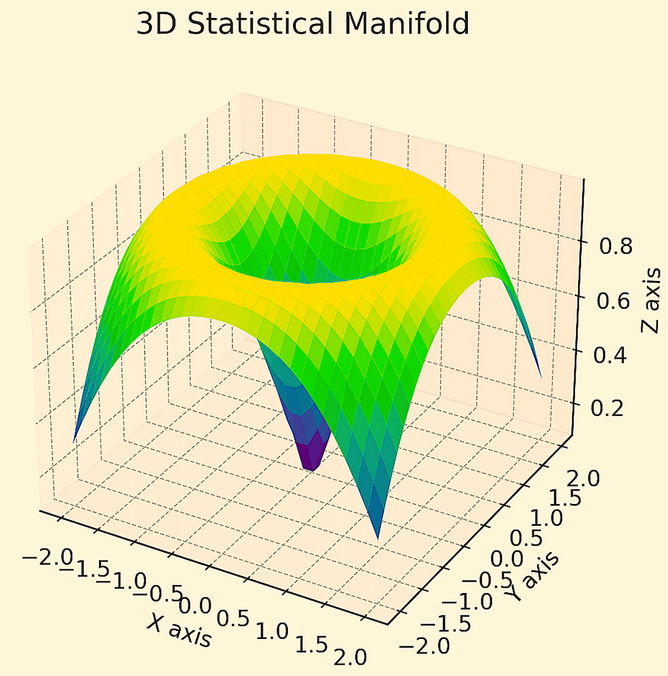
Exemple de codage - Géométrie différentielle
Voici un graphique en 3D représentant un collecteur statistique pour l'optimisation d'un portefeuille d'actifs financiers.
Chaque point du graphique représente un état possible d'un portefeuille composé de trois actifs différents. Les axes indiquent les rendements de ces actifs.
Cette visualisation aide à comprendre la nature multidimensionnelle des relations entre les actifs financiers et la dynamique des portefeuilles.

Code utilisé pour générer le graphique :
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Generate random data to sim returns of three financial assets
np.random.seed(17)
asset1_returns = np.random.normal(0.05, 0.15, 100)
asset2_returns = np.random.normal(0.07, 0.1, 100)
asset3_returns = np.random.normal(0.02, 0.05, 100)
# Create 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Scatterplot to rep the 3D statistical manifold
ax.scatter(asset1_returns, asset2_returns, asset3_returns, c='blue', marker='o')
# Labels & title
ax.set_xlabel('Asset 1 Returns')
ax.set_ylabel('Asset 2 Returns')
ax.set_zlabel('Asset 3 Returns')
ax.set_title('3D Statistical Manifold of Portfolio Optimization')
# Show plot
plt.show()Géométrie différentielle stochastique
La géométrie différentielle stochastique combine la géométrie différentielle (l'étude des formes lisses et de leurs propriétés) et le calcul stochastique (qui traite des systèmes influencés par des processus aléatoires) afin de modéliser et d'analyser des systèmes complexes et dynamiques tels que les marchés financiers.
Voici quelques-unes de ses principales applications :
Optimisation des portefeuilles sur des manifolds
L'optimisation traditionnelle des portefeuilles suppose souvent des relations linéaires entre les actifs, généralement modélisées dans des espaces euclidiens.
La géométrie différentielle stochastique étend cette hypothèse en permettant à l'optimisation de portefeuille de se produire sur des manifolds, qui sont des espaces courbes plus généraux.
Cette approche permet de saisir des relations et des dépendances plus complexes entre les actifs, ainsi que diverses interactions et contraintes non linéaires.
Modélisation du risque de queue
Le risque de queue fait référence au risque de pertes financières extrêmes, souvent sous-estimées dans des conditions de marché normales.
La géométrie différentielle stochastique permet de modéliser la dynamique des prix des actifs d'une manière qui rend mieux compte de la probabilité de ces événements rares et extrêmes.
Cela est possible grâce à l'utilisation d'équations différentielles sur des manifolds.
Cela permet une modélisation plus précise des queues lourdes souvent observées dans les distributions des rendements financiers.
Dynamique des prix des actifs sur les manifolds
Les marchés financiers sont complexes et présentent souvent des dynamiques non linéaires que les modèles standard ne parviennent pas à saisir.
En modélisant la dynamique des prix des actifs sur des plaines, la géométrie différentielle stochastique fournit un cadre pour comprendre ces complexités (si elle est bien modélisée).
Elle permet d'intégrer divers facteurs, tels que l'évolution de la volatilité du marché et des corrélations, dans un modèle cohérent et mathématiquement rigoureux.
Gestion des risques et tarification des produits dérivés
La géométrie différentielle stochastique permet de développer des modèles pour l'évaluation de produits dérivés complexes et la gestion des risques associés aux instruments financiers.
Ces modèles prennent en compte la courbure et la topologie de l'espace dans lequel les prix des actifs évoluent.
Pour les produits dérivés complexes, en particulier ceux dont les caractéristiques dépendent de la trajectoire ou ceux qui impliquent plusieurs actifs sous-jacents, la géométrie différentielle stochastique peut fournir un cadre permettant de saisir avec plus de précision la dynamique de leurs prix.
Apprentissage automatique et analyse de données
Dans le domaine de l'apprentissage automatique et de l'analyse des données, la géométrie différentielle stochastique permet d'analyser des espaces de données à haute dimension, courants dans la finance.
Elle fournit des méthodes pour comprendre la forme et la structure des données, ce qui est essentiel pour des tâches telles que la détection des anomalies, la reconnaissance des formes et la modélisation prédictive.
Analyse de la microstructure du marché
La compréhension de la microstructure des marchés, y compris le comportement du trading à haute fréquence et la dynamique du carnet d'ordres, peut bénéficier de l'application de la géométrie différentielle stochastique.
La géométrie différentielle stochastique peut offrir des modèles qui tiennent compte à la fois de la nature aléatoire du flux d'ordres et de la nature structurée de la profondeur du marché.
Stratégies de négociation à haute dimension
Le trading algorithmique implique souvent de prendre des décisions dans des espaces à haute dimension avec des relations complexes entre les variables.
La géométrie différentielle stochastique peut permettre de naviguer et d'optimiser les stratégies dans ces espaces.
Modélisation des surfaces de volatilité
La géométrie des surfaces de volatilité, qui représentent la manière dont la volatilité implicite varie en fonction du prix d'exercice et de l'échéance, peut être analysée à l'aide de la géométrie différentielle stochastique afin de mieux comprendre et prédire les changements dans la volatilité du marché.
Exemple : Tenseurs = Actifs, Manifold = Portefeuille, Courbure = Risque
Les actifs en tant que tenseurs
Imaginez que chaque actif ou classe d'actifs (comme les actions, les obligations, l'or, etc.) soit un "cube de données" multidimensionnel ou un tenseur.
) comme un "cube de données" multidimensionnel ou un tenseur. Ce tenseur contient toutes les variables et données qui influencent ses mouvements et ses rendements, comme l'historique des prix, la croissance, l'inflation, les primes de risque, les taux d'actualisation/taux d'intérêt, les corrélations, etc.
Analogie simple : Imaginez ce tenseur comme une feuille de calcul à plusieurs niveaux. Chaque couche (ou tranche) de la feuille de calcul pourrait représenter un attribut différent de l'actif, par exemple une couche pour les prix dans le temps, une autre pour la volatilité et une autre pour les facteurs externes tels que les indicateurs économiques. L'ensemble de ces couches donne une vue complète et multidimensionnelle de l'actif.
La configuration du portefeuille en tant que multiple
Imaginez maintenant l'univers entier des configurations de portefeuille possibles sous la forme d'une surface ou d'une forme, que nous appelons mathématiquement un "collecteur".
Chaque point de ce collecteur représente une combinaison spécifique de portefeuille, avec différentes répartitions de vos actifs ou classes d'actifs.
Analogie avec l'espace géométrique : Imaginez un paysage avec des collines, des vallées et des plateaux. Chaque point de ce paysage représente la façon dont vous avez réparti les différents actifs de votre portefeuille. La "hauteur" d'un point quelconque de ce paysage indique le rapport rendement/risque de cette composition spécifique du portefeuille.
Courbe et risque du portefeuille
Dans ce paysage, la courbure représente le risque. Les zones à forte courbure (comme les parties abruptes d'une colline) représentent un risque élevé, tandis que les zones plus plates (comme les plateaux) représentent un risque plus faible.
Interprétation simple : Si vous vous trouvez sur une colline escarpée, vous êtes plus susceptible de glisser et de tomber (risque élevé), alors que si vous vous trouvez sur un terrain plat, vous êtes beaucoup plus en sécurité (risque faible). En termes de portefeuille, se trouver dans une partie "abrupte" du collecteur signifie que de petits changements peuvent avoir un impact important sur vos rendements, ce qui indique un risque plus élevé. Les parties abruptes représentent des zones de forte concentration du portefeuille.
Objectif : forte hausse et faible courbure
Votre objectif dans ce paysage (multiple) est de trouver un endroit où vous êtes le plus haut possible (maximiser le ratio rendement/risque) tout en étant dans une zone de faible courbure (minimiser la sensibilité).
Un exemple de courbure acceptablement élevée pourrait être lorsque le risque de tomber loin n'est pas élevé (par exemple, une couverture prudente du risque, telle que des options coupant le risque de la queue gauche après un point).
Analogie du point idéal : Vous recherchez un plateau élevé ou une colline douce. Il s'agit d'une configuration de portefeuille dans laquelle vous avez réussi à maximiser vos rendements par rapport au risque tout en maintenant la sensibilité du portefeuille (courbure) à un niveau aussi bas que possible.
Approche mathématique
L'idée de base est de :
Définir le tenseur pour chaque actif
Mathématiquement, vous représenterez chaque actif sous la forme d'un tenseur qui encapsule ses facteurs d'influence et ses mesures de performance.
Cartographier les configurations de portefeuille sur le manifold
Construire un manifold où les points représentent les combinaisons de portefeuilles et où la géométrie (courbure) du manifold encode le risque.
Optimisation sur le collecteur
Utilisez les techniques de la géométrie différentielle pour trouver des points sur le collecteur qui optimisent les résultats souhaités (par exemple, en utilisant l'ascension en pente pour atteindre les points élevés tout en évitant les zones abruptes).
Brokers d'options
Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.
Hors ligne
- Utilisateurs enregistrés en ligne dans ce sujet: 0, invités: 1
- [Bot] ClaudeBot

