La géométrie de l'information dans la finance et le trading

Climax · 24-01-2024 23:22:19

La géométrie de l'information dans la finance, les marchés et le trading

La géométrie de l'information applique les concepts et les méthodes de la géométrie différentielle aux problèmes de la théorie des probabilités et des statistiques, qui sont importants en finance.

Elle explore la structure géométrique des modèles statistiques et étudie comment ces structures influencent les processus d'inférence et de prise de décision.

Le concept clé de la géométrie de l'information est la notion de collecteur statistique, qui est un espace géométrique où chaque point représente une distribution de probabilité.

Principaux enseignements :
➡️ La géométrie de l'information fournit un cadre mathématique permettant de visualiser et d'analyser des données financières complexes dans un espace multidimensionnel.
➡️ Elle permet de mieux comprendre les relations et les modèles nuancés et non linéaires des marchés financiers afin d'améliorer la prise de décision.
➡️ Aide les traders à analyser les données financières dans le contexte des manifolds statistiques.
➡️ En exploitant la courbure et la topologie de l'espace de données, la géométrie de l'information peut contribuer à diverses formes d'analyse (par exemple, l'optimisation).

Dans le contexte de la finance, la géométrie de l'information peut être appliquée de plusieurs façons :

Optimisation de portefeuille

L'une des applications les plus directes de la géométrie de l'information en finance est l'optimisation de portefeuille.

L'espace des portefeuilles potentiels peut être considéré comme un manifeste statistique, chaque point représentant une combinaison différente d'actifs.

Les méthodes de géométrie de l'information peuvent alors être utilisées pour comprendre la courbure et la structure de cet espace.

Cela permet de sélectionner des portefeuilles optimaux qui équilibrent le risque et le rendement d'une manière plus nuancée que les méthodes traditionnelles.

Gestion des risques

La géométrie de l'information peut aider à comprendre et à gérer les risques associés à différents instruments financiers.

En modélisant l'espace des facteurs de risque sous la forme d'un objet géométrique, on peut mieux comprendre les relations et les dépendances entre les différents risques, ce qui est important pour la gestion des risques et les stratégies d'atténuation.

Évaluation des options et produits dérivés

Dans l'évaluation des options et des produits dérivés, la géométrie de l'information peut être utilisée pour modéliser l'incertitude et la dynamique des actifs sous-jacents.

L'approche géométrique peut fournir de nouvelles perspectives sur les sensibilités des prix des options à divers facteurs (comme la volatilité, les taux d'intérêt, etc.), conduisant à des modèles d'évaluation potentiellement plus robustes.

Trading algorithmique

La géométrie de l'information peut être appliquée au développement d'algorithmes de trading.

En comprenant les propriétés géométriques des données du marché, ces algorithmes peuvent potentiellement identifier des modèles et des tendances qui ne sont pas immédiatement visibles par les méthodes statistiques traditionnelles.

Indicateurs économiques et modélisation macroéconomique

La géométrie de l'information peut également être appliquée à la modélisation des indicateurs économiques et des facteurs macroéconomiques, et contribuer à la construction de modèles qui reflètent plus précisément la dynamique des systèmes économiques.

Manifolds statistiques et utilisation dans le trading

En géométrie de l'information, un manifold statistique est un espace géométrique dans lequel chaque point représente une distribution de probabilité.

Ce concept repose sur l'idée que les distributions de probabilités peuvent être paramétrées et donc être considérées comme des points dans un espace géométrique.

La géométrie de cet espace est définie en termes de métrique d'information de Fisher, qui permet de mesurer les distances entre les distributions de probabilités.

Exemple d'un collecteur statistique

Prenons l'exemple d'un portefeuille de 5 actifs où chaque actif (ou flux de rendement) présente des risques et des rendements égaux et où tous les actifs ne sont pas corrélés les uns aux autres.

Ce graphique montre que si vous concentrez votre risque sur un seul des cinq actifs, vous obtiendrez un mauvais rapport rendement/risque - représenté par la forte courbure de l'espace.

En revanche, si vous les diversifiez davantage, vous vous retrouverez dans une partie plus plate de l'espace, ce qui représente un meilleur rapport rendement/risque.

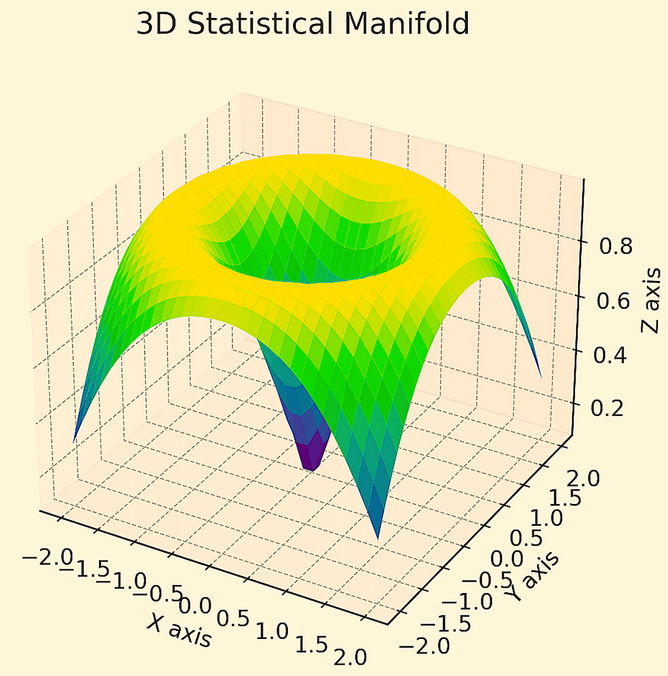
Chaque point du graphique représenterait une distribution de probabilité théorique d'une certaine combinaison d'actifs.

En outre, s'il s'agissait d'un scénario de "probabilités de probabilités" dans lequel les probabilités elles-mêmes ne sont pas bien connues - comme c'est souvent le cas sur les marchés - nous aurions des structures de probabilité d'ordre supérieur.

Au lieu d'un plan 2D incurvé dans un espace 3D, nous aurions des couches supplémentaires de dimensionnalité et nous optimiserions ensuite cette structure.

Comprendre le manifold statistique

Paramétrage des distributions de probabilités

Considérons une famille de distributions de probabilités paramétrées par un ensemble de paramètres (comme la moyenne et la variance dans une distribution normale).

Chaque ensemble de paramètres correspond à une distribution de probabilités unique, et donc à un point du collecteur statistique.

Métrique d'information de Fisher

La métrique d'information de Fisher permet de mesurer la "distance" entre différentes distributions de probabilités (ou points) sur le manifold.

Cette métrique est définie en termes de sensibilité de la distribution de probabilité aux changements de ses paramètres.

En termes simples, elle mesure à quel point la distribution de probabilités change lorsque l'on modifie légèrement ses paramètres.

Géodésiques

Le chemin le plus court entre deux points (distributions) d'un manifold est appelé géodésique.

Dans le contexte des manifolds statistiques, ces géodésiques représentent le moyen le plus efficace de passer d'une distribution de probabilités à une autre en termes de changement d'information.

Domaines mathématiques connexes

La géométrie de l'information est liée à plusieurs autres domaines mathématiques.

En les intégrant à la géométrie de l'information, on peut obtenir une approche complète et solide de la modélisation et de l'analyse financières.

Voici un aperçu des domaines mathématiques connexes et des méthodes supplémentaires qui peuvent être employées :

Géométrie différentielle

Il s'agit du fondement mathématique de la géométrie de l'information.

Elle traite des propriétés des courbes et des surfaces et étend ces concepts à des dimensions supérieures.

La géométrie différentielle fournit les outils permettant de définir et d'analyser la courbure et la topologie des manifolds statistiques.

Probabilité et statistiques

La géométrie de l'information applique les concepts de la géométrie différentielle à la théorie des probabilités, principalement dans le contexte de l'inférence statistique et de l'estimation.

Algèbre linéaire

L'algèbre linéaire est utile pour comprendre la structure des données et des modèles. Elle est également utile dans les espaces à haute dimension.

La décomposition des valeurs propres et la décomposition des valeurs singulières sont des techniques clés de l'algèbre linéaire qui trouvent des applications en finance.

Calcul des variations et théorie du contrôle optimal

Ces domaines fournissent des méthodes pour trouver des chemins ou des stratégies optimales, un peu comme la recherche de chemins géodésiques en géométrie de l'information.

Analyse numérique

Les méthodes numériques sont essentielles pour mettre en œuvre les modèles et résoudre les équations qui apparaissent en géométrie de l'information, en particulier lorsqu'il s'agit de données à haute dimension.

Triangulation avec d'autres méthodes

En combinant la géométrie de l'information avec ces domaines et méthodes mathématiques connexes, un trader quantique peut développer une compréhension plus nuancée et à multiples facettes des phénomènes financiers, ce qui peut conduire à une meilleure prise de décision et à de meilleurs modèles financiers.

Apprentissage automatique et science des données

Des techniques telles que les réseaux neuronaux, l'analyse de régression et le regroupement peuvent fournir des informations empiriques qui complètent les modèles théoriques de la géométrie de l'information.

Ces méthodes sont particulièrement utiles pour la reconnaissance des formes, la modélisation prédictive et la classification des risques.

Analyse des séries temporelles

Les méthodes d'analyse des séries temporelles peuvent aider à comprendre et à prédire la dynamique temporelle des marchés, ce qui peut être important pour valider les modèles développés à l'aide de la géométrie de l'information.

Économétrie

Comprendre les facteurs économiques qui influencent les marchés financiers et tester des hypothèses sur le comportement des marchés.

Finance comportementale

Ce domaine étudie les facteurs psychologiques qui influencent le comportement des traders et des investisseurs.

L'intégration des connaissances de la finance comportementale peut fournir une vision plus holistique, en particulier dans les modèles qui pourraient autrement supposer un comportement rationnel.

Techniques de gestion des risques

Des outils tels que la valeur à risque (VaR), la valeur à risque conditionnelle (CVaR) et les tests de résistance sont essentiels pour évaluer et gérer les risques identifiés par les modèles de géométrie de l'information.

Processus stochastiques et théorie de la marche aléatoire

Les processus stochastiques sont utiles pour modéliser le caractère aléatoire inhérent aux marchés financiers, et leur intégration peut valider ou remettre en question les hypothèses des modèles géométriques de l'information.

Théorie de l'optimisation

Particulièrement pertinente pour l'optimisation des portefeuilles et les problèmes d'allocation des ressources en finance, en s'appuyant sur des techniques d'optimisation linéaires et non linéaires.

Nous consacrerons le reste de l'article à l'application de la géométrie de l'information à la construction de portefeuilles.

Nous utiliserons l'exemple de la parité des risques ou de l'allocation à bêta équilibré.

Utilisation de la géométrie de l'information dans les cadres de négociation (exemple : la parité des risques)

L'intégration de concepts tels que les collecteurs statistiques et la géométrie de l'information dans un cadre de parité des risques (en particulier dans le contexte de l'équilibrage des allocations afin d'éviter les biais environnementaux en faveur des conditions d'inflation et de croissance actualisées) implique une certaine approche.

Voici comment celle-ci peut être structurée.

Modélisation de l'environnement à l'aide de plis statistiques

La stratégie de parité des risques diffère de l'optimisation traditionnelle des portefeuilles en ce qu'elle se concentre non seulement sur les rendements attendus des actifs, mais aussi, et surtout, sur la répartition des risques.

L'intégration de concepts tels que les manifolds statistiques et la géométrie de l'information peut améliorer la compréhension et la mise en œuvre des stratégies de parité des risques.

Dimensions environnementales

Créez un collecteur statistique où chaque dimension représente une variable économique clé qui fait partie de ce cadre :

inflation actualisée
conditions de croissance actualisées
primes de risque
taux d'actualisation

Cartographie des classes d'actifs

Positionnez chaque classe d'actifs dans ce collecteur en fonction de sa sensibilité et de sa réaction à ces variables.

On peut d'abord penser à un cadre en deux dimensions :

Distance ajustée au risque

Utilisez les principes de la géométrie de l'information pour évaluer la "distance" entre les classes d'actifs dans un espace ajusté au risque.

Cela permet de comprendre les avantages de la diversification et la contribution au risque de chaque classe d'actifs dans des conditions économiques différentes.

Allocation dynamique

Actualiser régulièrement l'allocation du portefeuille en fonction de l'évolution de la géométrie du collecteur, qui reflète les changements dans les conditions économiques et les sensibilités des classes d'actifs.

Dynamique du risque

La géométrie du collecteur peut illustrer la manière dont la dynamique du risque des différentes classes d'actifs évolue en fonction de différents scénarios de marché, tels que les variations de l'inflation ou de la croissance économique.

Structure de corrélation

La courbure et les autres propriétés géométriques du collecteur peuvent donner un aperçu de la structure de corrélation entre les classes d'actifs.

Cet aspect est important dans les stratégies de parité des risques, car il permet de s'assurer que les risques ne sont pas concentrés, mais répartis entre différents actifs dans différentes dimensions (diversification par classe d'actifs, par pays et par devise).

Mise en œuvre pratique dans la gestion de portefeuille

Sélection des catégories d'actifs

Choisissez des catégories d'actifs dont la sensibilité à l'inflation, à la croissance, aux primes de risque et aux taux d'actualisation varie afin d'assurer une large couverture du collecteur.

Les zones à forte courbure d'un collecteur peuvent indiquer des classes d'actifs très sensibles à l'évolution des conditions économiques.

Comme nous l'avons montré graphiquement dans une section précédente, une forte courbure dans un collecteur signifie que le portefeuille est très sensible aux changements des conditions économiques et de marché.

Par exemple, si vous concentrez votre portefeuille sur n'importe quoi - actions, obligations, pétrole, etc. - vous connaîtrez des hauts et des bas importants par rapport à un portefeuille plus diversifié qui extrait plus efficacement les primes de risque du marché.

Optimisation de la parité des risques

Ajustez le portefeuille de manière à ce que la contribution au risque de chaque catégorie d'actifs corresponde à la performance attendue dans les conditions économiques actuelles.

Tenez compte à la fois du risque absolu de chaque actif et de sa prime de risque relative.

Vous pouvez augmenter la part d'un actif si vous êtes rémunéré par rapport à son risque et par rapport au fait qu'il déséquilibre le portefeuille.

En d'autres termes, si une classe d'actifs présente une prime de risque élevée qui est suffisamment compensée en termes de risque ajusté, augmentez son allocation.

À l'inverse, il convient de réduire la part des classes d'actifs présentant une faible prime de risque ou une forte sensibilité aux conditions économiques défavorables.

Suivi continu

Utiliser la structure du collecteur pour surveiller en permanence la façon dont les changements des conditions économiques affectent le profil risque-rendement du portefeuille.

Il s'agirait de suivre les mouvements des classes d'actifs au sein du collecteur en fonction de l'évolution des variables économiques.

Analyse de scénarios et tests de résistance

Effectuer des analyses de scénarios pour comprendre comment le portefeuille se comporterait dans diverses conditions économiques, telles qu'une inflation élevée ou des périodes de faible croissance.

Cette méthode permet de s'assurer que le portefeuille est positionné de manière à tirer parti des risques compensés (comme les primes de risque élevées) tout en conservant un profil de risque équilibré et diversifié.

Géométrie de l'information dans la construction de portefeuilles

Mesurer la diversification

La géométrie de l'information peut aider à quantifier le degré de diversification d'un portefeuille.

La distance entre les points (représentant différentes combinaisons d'actifs) dans le collecteur peut indiquer à quel point ils sont similaires ou différents en termes de risque.

L'effet de levier

Dans certains cas, il est possible d'appliquer un effet de levier aux catégories d'actifs à faible risque afin d'égaliser leur contribution au risque par rapport aux catégories d'actifs à risque plus élevé.

Par exemple, les obligations d'État ont tendance à être peu risquées et à faible rendement.

Mais elles peuvent être transformées en actifs à haut risque et à haut rendement, comme les actions, en appliquant un effet de levier ou des techniques similaires (par exemple, les contrats à terme, les options, les swaps).

Il s'agit d'un type d'ingénierie financière qui permet d'obtenir des flux d'actifs ou de rendements à risque égal.

Suivi continu et rééquilibrage

Contrôler régulièrement le portefeuille pour s'assurer que les contributions au risque restent équilibrées.

Autres formes d'analyse (par exemple, l'analyse topologique des données)

La topologie algébrique, en particulier l'analyse topologique des données, peut être utilisée pour identifier des schémas complexes dans des données financières à haute dimension, par exemple pour identifier des groupes d'actifs qui se comportent de manière similaire.

Courtiers pour investir en bourse

Investir comporte des risques de perte

#1 24-01-2024 23:22:19