#1 28-01-2024 17:34:48

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 299

La topologie différentielle dans la finance, les marchés et le trading

La topologie différentielle est un domaine des mathématiques qui s'intéresse à l'étude des fonctions et des ensembles différentiables.

Elle comporte plusieurs concepts clés qui peuvent être appliqués théoriquement et pratiquement à la finance et aux marchés, principalement sous la forme d'une interprétation visuelle avancée des données.

Principaux enseignements

Flexibilité du modèle

• La topologie différentielle permet de modéliser des instruments financiers complexes et la dynamique des marchés.

• Elle s'adapte aux relations non linéaires et complexes.

Analyse de la surface du risque

• Permet une compréhension plus approfondie des paysages de risque.

Interprétation avancée des données

• Offre des méthodes sophistiquées pour interpréter les données financières à haute dimension.

• Révèle des informations que les modèles standard pourraient manquer.

• La visualisation topologique des données peut être utile pour explorer des ensembles de données financières complexes de manière plus intuitive.

Exemples de codage

• Vous trouverez ci-dessous quelques exemples de codage.

Concepts clés de la topologie différentielle en finance, marchés et trading

Explorons quelques-uns de ces concepts et leurs applications potentielles :

Manifolds

En topologie différentielle, un manifold est un espace qui ressemble localement à l'espace euclidien.

Les marchés financiers peuvent être vus comme des manifolds, où chaque point du manifold représente, par exemple, un état du marché ou un portefeuille défini par divers paramètres.

Comprendre la structure manifold des marchés peut aider à comprendre comment différentes conditions de marché ou combinaisons d'actifs sont interconnectées.

Espaces tangents et vecteurs

En chaque point d'un manifold, il existe un espace tangent, un espace vectoriel composé des vecteurs tangents en ce point.

En finance, les vecteurs tangents peuvent représenter des directions ou des changements possibles sur le marché à un moment donné, tels que des mouvements de prix ou des changements de volatilité.

Formes différentielles et intégration

Les formes différentielles étendent le concept de fonctions et d'intégrales à des dimensions supérieures.

Elles peuvent être utilisées en finance pour des intégrations complexes sur des manifolds financiers, comme l'intégration de la distribution de probabilité de rendement d'un portefeuille dans différentes conditions de marché.

Champs et flux vectoriels

Un champ de vecteurs attribue un vecteur tangent à chaque point d'un manifold, représentant une direction.

En finance, un champ vectoriel peut modéliser la direction dans laquelle un marché évolue sous l'effet de diverses forces, comme les indicateurs économiques ou le sentiment.

La compréhension de ces champs peut aider à prédire les tendances du marché ou à élaborer des stratégies de trading algorithmique.

Théorie de Morse

La théorie de Morse étudie la topologie des plis à l'aide de fonctions lisses.

En finance, la théorie de Morse pourrait être utilisée pour analyser les topologies des données du marché.

Cela permet d'identifier les points critiques - comme l'optimisation du rapport risque-rendement dans un portefeuille ou une concentration extrême du risque - et de comprendre comment différentes décisions d'allocation d'actifs passent de l'un à l'autre de ces points.

Dans les cadres risque-rendement, les points abrupts indiquent généralement des zones où le portefeuille est plus risqué ou plus sensible à l'évolution des conditions économiques (par exemple, la région bleue ci-dessous), tandis que les régions plus plates représentent généralement des allocations d'actifs où le portefeuille est moins sensible à l'évolution des conditions du marché (par exemple, la région jaune).

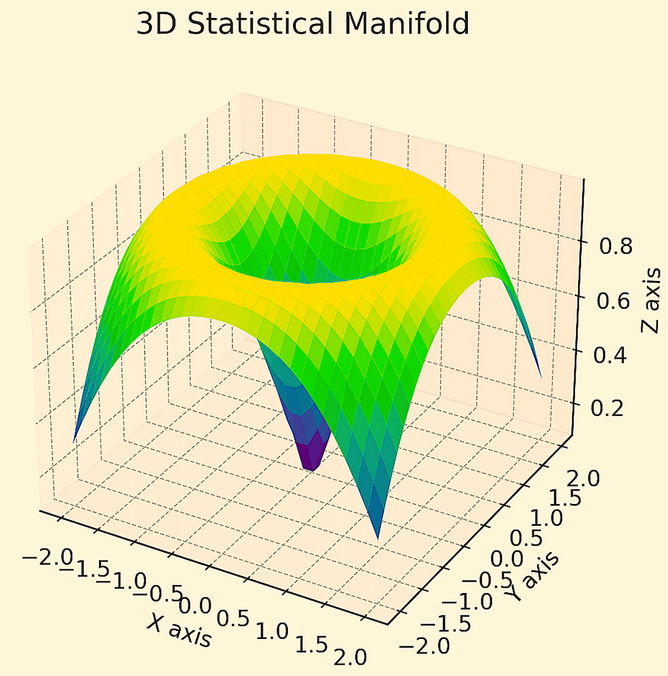
Lorsque les données financières/de marché sont présentées dans un sens géométrique ou topologique, elles favorisent généralement l'idée de diversification et de non-dépendance à l'égard d'un seul flux de rendement dans un portefeuille - en veillant à ce que les flux de rendement soient réellement différenciés/non-corrélés.

Manifolds stables et instables

Ces concepts sont utilisés pour comprendre le comportement des systèmes dynamiques près des points d'équilibre.

Sur les marchés financiers, ils peuvent être appliqués pour étudier la stabilité des équilibres de marché et la façon dont les marchés réagissent aux perturbations, telles que les chocs économiques ou les changements de politique.

Homologie et homotopie

Il s'agit de méthodes de topologie utilisées pour classer et analyser les formes des espaces.

• Homologie - Mesure et analyse les formes et la connectivité des espaces topologiques.

• Homotopie - étudie les déformations continues entre les espaces topologiques (c'est-à-dire la façon dont les formes se transforment en douceur les unes dans les autres).

En finance, elles pourraient théoriquement être utilisées pour analyser et classer différents régimes de marché, allocations d'actifs et stratégies de trading/investissement afin de comprendre leurs caractéristiques et différences fondamentales.

Faisceaux de fibres et connexions

Ces concepts traitent des moyens de "coller ensemble" systématiquement divers collecteurs.

Sur les marchés, ils pourraient être utilisés pour décrire l'interconnexion de différents marchés ou instruments financiers et la manière dont les changements dans un domaine peuvent en influencer un autre.

Applications de la topologie différentielle au trading

Le lien n'est peut-être pas immédiatement évident, car la topologie différentielle est un domaine très abstrait, mais ses concepts peuvent être appliqués pour modéliser et comprendre des systèmes et des instruments financiers complexes.

Voici quelques exemples d'applications :

Modélisation des marchés et instruments financiers

La topologie différentielle peut être utilisée pour modéliser la structure complexe des marchés et des instruments financiers.

Par exemple, le concept de manifold peut être utile pour comprendre la nature multidimensionnelle des marchés financiers, où chaque dimension représente un aspect ou une variable différente du marché, comme la croissance, l'inflation, les taux d'actualisation/taux d'intérêt, les primes de risque.

Gestion du risque et optimisation du portefeuille

Les aspects géométriques et topologiques de la topologie différentielle peuvent être utilisés dans la gestion des risques et l'optimisation des portefeuilles.

Par exemple, la courbure d'un collecteur pourrait représenter le profil de risque d'un portefeuille, l'objectif étant de naviguer dans ce manifold de manière à optimiser les rendements tout en minimisant les risques.

Dynamique des marchés et analyse comportementale

Par exemple, le comportement des acteurs du marché et l'évolution des prix des actifs dans le temps peuvent être modélisés comme des systèmes dynamiques sur des plaines.

Cela permet d'étudier leur stabilité et leur évolution dans différentes conditions.

Trading algorithmique et quantitatif

Dans le cadre du trading algorithmique, la topologie différentielle peut être utilisée pour modéliser et prédire les mouvements du marché et pour développer des stratégies de trading.

Les techniques de topologie différentielle peuvent aider à comprendre la structure des données financières et à concevoir des algorithmes pour en tirer parti.

Fixation du prix des produits financiers dérivés

Les aspects géométriques de la topologie différentielle peuvent s'avérer utiles dans l'évaluation des produits financiers dérivés complexes.

Par exemple, la compréhension de la topologie de l'espace des trajectoires possibles que le prix d'un actif sous-jacent peut prendre peut aider à améliorer la modélisation et la tarification des produits dérivés.

Tests de résistance et analyse de scénarios

La topologie différentielle peut être utilisée dans les tests de résistance et l'analyse de scénarios en fournissant un cadre permettant de comprendre comment différentes conditions de marché ou différents facteurs externes peuvent affecter le système financier.

Comprendre les crises du marché

La topologie différentielle permet de comprendre la structure et la dynamique des crises financières et des anomalies de marché en aidant à modéliser les interactions complexes et les boucles de rétroaction qui sont souvent présentes dans de telles situations.

Topologie différentielle et géométrie différentielle sur les marchés

La topologie différentielle se concentre sur les propriétés qualitatives et les "caractéristiques globales" des structures géométriques.

Elle étudie la forme et la connectivité des marchés financiers sans s'intéresser à des paramètres spécifiques.

Elle est utile pour comprendre l'analyse des données topologiques et les modèles de marché.

La géométrie différentielle, quant à elle, s'intéresse aux aspects quantitatifs de ces structures, comme la courbure et les angles.

Elle offre des moyens précis de modéliser les trajectoires des marchés, la courbure des risques et les mouvements de prix des actifs.

Alors que la topologie offre une vision large et qualitative, la géométrie fournit un cadre détaillé et quantitatif, tous deux essentiels à l'analyse financière globale et à l'élaboration de stratégies en matière de négociation et de marchés.

Topologie différentielle et topologie algébrique

La topologie différentielle est principalement utilisée pour modéliser et comprendre les dynamiques de marché lisses et continues.

Elle permet de visualiser et d'analyser les tendances et les modèles du marché en temps continu ou sur des surfaces fluides (les surfaces peuvent représenter la topologie du marché/des données financières/économiques).

La topologie algébrique est utile pour analyser les réseaux et les relations financières complexes.

Elle permet de comprendre la structure globale et la connectivité des systèmes financiers, par exemple la manière dont les différentes entités financières sont reliées entre elles ou la robustesse des réseaux financiers.

Exemple de codage - Topologie différentielle sur les marchés

La création d'un collecteur dans le contexte de la topologie différentielle à l'aide de Python nécessite la génération (dans ce cas) d'un ensemble de données synthétiques représentant un espace à haute dimension.

Sur les marchés financiers, cela pourrait s'apparenter à la simulation d'un ensemble d'indicateurs financiers ou de prix d'actifs et de toutes les influences qui affectent leurs résultats au fil du temps.

Nous utiliserons NumPy pour créer ces données synthétiques, puis pour en visualiser une représentation en basse dimension, que l'on peut considérer comme un "manifold" simplifié.

Pour cet exemple, simulons les données d'un scénario de marché hypothétique à l'aide d'une distribution gaussienne multidimensionnelle.

Nous utiliserons ensuite le t-SNE (t-Distributed Stochastic Neighbor Embedding), une technique de manifold learning, pour visualiser les données à haute dimension dans un espace bidimensionnel.

Le t-SNE est utile pour capturer la structure locale des données à haute dimension et pour intégrer cette structure dans des dimensions inférieures.

Voici un peu de code Python pour y parvenir :

Exemple 1

import numpy as np
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE

# Generate synthetic high-dimensional market data
np.random.seed(56)
n_samples = 1000
n_features = 50 # Number of features to simulate complex market scenario
data = np.random.normal(0, 1, (n_samples, n_features))

# Apply t-SNE for manifold learning
tsne = TSNE(n_components=2, perplexity=30, n_iter=300)
data_2d = tsne.fit_transform(data)

# Visualizing the manifold
plt.figure(figsize=(10, 6))
plt.scatter(data_2d[:, 0], data_2d[:, 1])
plt.title("2D Visualization of a High-Dimensional Synthetic Market Manifold")
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.show()

Exemple 2

from sklearn.decomposition import PCA

# Apply PCA for dimensionality reduction
pca = PCA(n_components=2)
data_2d_pca = pca.fit_transform(data)

# Visualizing the manifold with PCA
plt.figure(figsize=(10, 6))
plt.scatter(data_2d_pca[:, 0], data_2d_pca[:, 1])
plt.title("2D Visualization of a High-Dimensional Synthetic Market Manifold using PCA")
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")
plt.show()

Cette représentation est illustrée dans la section ci-dessous.

Représentation en 2D

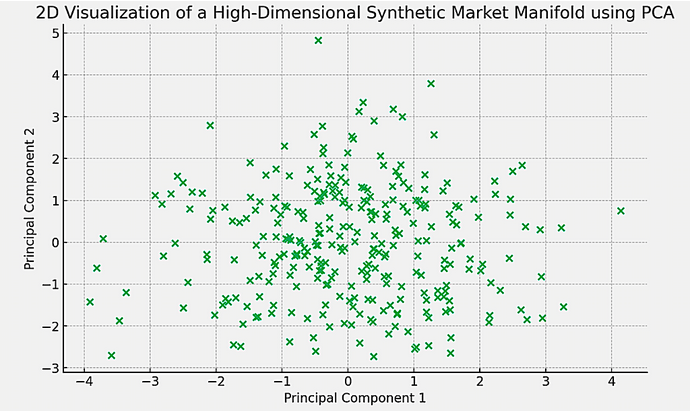
Ci-dessus, la visualisation en 2D des données synthétiques du marché en haute dimension à l'aide de l'ACP (Analyse en Composantes Principales).

Chaque point du graphique représente une observation de l'espace original à haute dimension projetée sur les deux premières composantes principales.

Cette visualisation peut aider à identifier des modèles ou des groupes dans les données et fournir des informations sur la structure du scénario du marché synthétique.

Représentation 3D

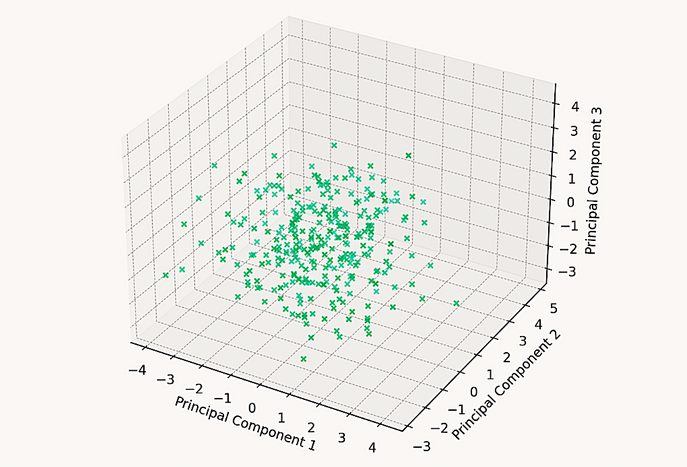
Voici la visualisation en 3D des données synthétiques du marché en haute dimension à l'aide de l'ACP (Analyse en Composantes Principales).

Ce graphique représente la projection des données originales sur les trois premières composantes principales.

Il fournit une vue plus nuancée de la structure des données et peut potentiellement révéler des groupes, des tendances ou des relations qui pourraient ne pas être apparentes dans des représentations de dimensions inférieures.

Le code correspondant est présenté ci-dessous (il utilise les mêmes bibliothèques que celles énumérées dans le code ci-dessus) :

# PCA for 3D dimensionality reduction
pca_3d = PCA(n_components=3)
data_3d_pca = pca_3d.fit_transform(data)

# Visualize the manifold in 3D
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(data_3d_pca[:, 0], data_3d_pca[:, 1], data_3d_pca[:, 2])

ax.set_title("3D Visualization of a High-Dimensional Synthetic Market Manifold using PCA")
ax.set_xlabel("Principal Component 1")
ax.set_ylabel("Principal Component 2")
ax.set_zlabel("Principal Component 3")
plt.show()

Conclusion

Bien que ces applications soient théoriquement possibles, l'application pratique de la topologie différentielle en finance nécessite une compréhension approfondie des mathématiques avancées et de la théorie financière.

Ce domaine est plus couramment utilisé dans le monde universitaire et dans la recherche théorique que dans le trading quotidien ou la prise de décision financière.

Néanmoins, de plus en plus de "mathématiques pures" sont appliquées à la finance quantitative et aux algorithmes financiers afin d'ouvrir de nouvelles voies et d'obtenir un avantage en matière de trading.

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.