#1 31-12-2023 19:38:06

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 109

Processus stochastiques sur les marchés financiers (composants, formes)

Les processus stochastiques sont des modèles mathématiques utilisés pour prédire la probabilité de divers résultats dans le temps, en tenant compte des variables aléatoires et des inconnues.

En finance, ils sont utilisés pour prévoir les tendances du marché et les prix des actifs, aidant ainsi les traders/investisseurs à prendre des décisions éclairées et à gérer les risques de manière efficace.

       

Principaux enseignements

Comprendre l'incertitude

• Les processus stochastiques sont utilisés pour modéliser le comportement des prix des actifs, des taux d'intérêt et d'autres instruments financiers.

• Ils fournissent un cadre mathématique pour l'analyse et la prévision des trajectoires futures probables des prix.

Gestion du risque

• Permet aux analystes financiers d'estimer la probabilité de différents résultats sur les marchés.

• Elle aide à fixer le prix des titres dérivés.

Optimisation des stratégies de trading et d'investissement

• Les processus stochastiques contribuent à l'optimisation des stratégies via la simulation de différents scénarios -> évaluation de l'impact potentiel sur les portefeuilles.

• Nous couvrons différentes techniques ci-dessous.

Composantes d'un processus stochastique

Un processus stochastique est caractérisé par plusieurs composantes :

1) Espace d'état

L'ensemble de tous les résultats ou états possibles que le processus peut prendre.

Exemple

Dans la modélisation des cours boursiers, l'espace d'états pourrait être la gamme possible des prix que l'action peut avoir.

2) Ensemble d'indices

Le paramètre qui définit la progression du temps ou de l'espace dans le processus.

Exemple

Dans une analyse de séries chronologiques, l'ensemble d'indices peut être discret (jours, mois) ou continu (temps en secondes).

3) Variables aléatoires

Variables pouvant prendre différentes valeurs avec certaines probabilités, représentant le caractère aléatoire inhérent au processus.

Exemple

Les rendements quotidiens d'une action, où le rendement de chaque jour est une variable aléatoire.

4) Réalisations

Résultats ou séquences spécifiques générés par le processus stochastique.

Exemple

Une trajectoire particulière des prix des actions sur une année, représentant une réalisation du processus stochastique.

5) Mesure de probabilité

Fonction mathématique qui attribue des probabilités aux différents résultats ou séquences du processus.

Exemple

La distribution de probabilité des rendements boursiers, qui quantifie la probabilité de différents niveaux de rendement.

La compréhension de ces composantes permet aux analystes et aux chercheurs de construire des modèles capables de simuler et d'analyser des systèmes complexes, tels que les marchés financiers, qui présentent un certain degré d'incertitude et d'aléa.

Formes de processus stochastiques et applications à la finance

Voici différentes formes de processus stochastiques ainsi que des exemples d'application à la finance :

Marche aléatoire

Processus dans lequel chaque étape est déterminée par une variable aléatoire, sans aucun schéma prévisible.

Exemple

Sur le marché boursier, une marche aléatoire suggère que les mouvements ou tendances passés ne peuvent pas être utilisés pour prédire les mouvements futurs, ce qui implique que les prix des actions sont essentiellement aléatoires et ne sont pas influencés par les tendances passées.

Mouvement brownien géométrique (ou processus de Wiener)

Processus stochastique à temps continu caractérisé par des trajectoires continues et des incréments indépendants, normalement distribués.

Le mouvement brownien est à la base de plusieurs autres processus stochastiques, en particulier dans le modèle d'évaluation des options de Black-Scholes.

Exemple

Souvent utilisé dans l'évaluation des produits financiers dérivés, où il aide à modéliser le comportement aléatoire des prix des actifs dans le temps.

Processus de Poisson

Processus de comptage dans lequel le nombre d'événements survenant dans un intervalle de temps est une variable aléatoire de Poisson, et le temps entre les événements successifs a une distribution exponentielle.

Exemple

Utilisé dans la modélisation du risque de crédit pour prédire le nombre de défaillances au sein d'un portefeuille de prêts sur une certaine période, en supposant un taux moyen de défaillance constant.

Chaîne de Markov

Une chaîne de Markov est un processus stochastique dans lequel la probabilité de transition vers un état particulier dépend uniquement de l'état actuel et du temps écoulé, et non de la séquence d'événements qui l'a précédé.

Exemple

Utilisée pour modéliser les variations de taux d'intérêt lorsque le taux d'intérêt futur dépend uniquement du taux actuel et non du chemin parcouru pour atteindre le taux actuel (par exemple, le modèle CIR, le modèle BDT, le modèle Chen).

Martingale et Semimartingale

Une séquence de variables aléatoires où la valeur attendue de l'observation suivante, compte tenu de toutes les observations passées, est égale à l'observation actuelle.

Une semimartingale est un processus stochastique plus général qui inclut les martingales et autorise la dérive, ce qui signifie que la valeur attendue peut changer au fil du temps.

Par exemple, le cours d'une action peut être considéré comme une semimartingale, car vous vous attendez à un rendement positif (dérive) au fil du temps, car c'est l'idée qui sous-tend la détention d'une action : obtenir un rendement attendu positif au fil du temps.

Exemple

Dans le contexte des marchés financiers, une martingale représente un jeu équitable, où aucune information ou analyse ne peut donner un avantage à un investisseur/trader. Cela implique que la meilleure prédiction du prix de demain est le prix d'aujourd'hui.

Le prix d'un actif financier sur un marché avec des coûts de transaction est un exemple de semi-martingale. Le processus de prix comprend à la fois une tendance prévisible (dérive) et une composante aléatoire imprévisible.

Processus de Levy

Processus qui généralise le mouvement brownien et les processus de Poisson et qui se caractérise par des incréments stationnaires et indépendants.

Exemple

Utilisé dans la modélisation des rendements boursiers et des mouvements de prix.

Particulièrement utilisé en présence de sauts ou de changements soudains, il offre une représentation plus réaliste des marchés financiers.

Processus d'Ornstein-Uhlenbeck

Processus de retour à la moyenne souvent utilisé pour modéliser les taux d'intérêt et d'autres variables financières.

Exemple

Employé dans l'évaluation des produits dérivés de taux d'intérêt.

Permet de modéliser l'évolution des taux d'intérêt qui tendent à revenir à une moyenne à long terme.

Processus de diffusion par bonds

Processus qui incorpore à la fois des trajectoires continues et des sauts.

Souvent utilisé pour modéliser les prix des actifs qui peuvent connaître des sauts soudains en raison de nouvelles ou d'événements.

Exemple

Utilisé dans l'évaluation des options pour intégrer la possibilité de changements soudains et importants dans les prix des actifs.

Processus de Hawkes

Processus ponctuel auto-excitant utilisé pour modéliser des événements regroupés dans le temps.

Souvent utilisé dans l'analyse des données financières à haute fréquence.

Exemple

Utilisé dans la modélisation des stratégies de trading à haute fréquence.

Il permet de comprendre le regroupement des transactions ou des cotations.

Peut être utilisé pour prédire les périodes de forte activité.

Mouvement brownien fractionnaire

Généralisation du mouvement brownien qui intègre la mémoire dans le processus.

Caractérisé par un paramètre de Hurst qui mesure le degré de mémoire.

Exemple

Utilisé dans la modélisation de séries temporelles financières avec une dépendance à long terme.

Il permet de saisir des structures et des corrélations plus complexes dans les données financières.

Théorie des files d'attente

Concerne l'étude des lignes d'attente ou des files d'attente.

Elle utilise des processus stochastiques pour modéliser l'heure d'arrivée des entités et le temps nécessaire pour les servir.

Exemple

Appliquée à l'optimisation des algorithmes de trading.

Aide à comprendre et à minimiser la latence et le dérapage associés à l'exécution d'ordres importants.

En d'autres termes, les applications concernent les coûts de transaction.

Modèle de Markov caché (MMC)

Un modèle statistique de Markov dans lequel le système modélisé est un processus de Markov avec des états non observés (cachés).

Le terme "caché" dans MMC fait référence au fait que la séquence d'états réelle que traverse le système n'est pas directement observable.

Il ne peut être déduit que des données observables.

Exemple

Comme cela est un peu abstrait, prenons d'abord un exemple plus concret.

Imaginez que vous avez un ami qui vit dans un endroit où il pleut ou il fait beau tous les jours, mais vous ne pouvez pas voir directement le temps qu'il fait.

Cependant, chaque jour, votre ami porte soit un parapluie, soit des lunettes de soleil. En observant si votre ami porte un parapluie ou des lunettes de soleil pendant plusieurs jours, vous pouvez faire une supposition sur le temps qu'il fera (état caché) ces jours-là.

La météo est l'état caché et l'accessoire (parapluie ou lunettes de soleil) est la donnée observable.

Dans le contexte du trading algorithmique, les MMC peuvent être utilisés pour modéliser les états cachés du marché.

Ces états cachés peuvent représenter différentes conditions du marché, comme la "peur" ou la "cupidité".

Les données observables dans ce cas peuvent être les cours des actions, les volumes de transactions ou d'autres indicateurs de marché.

En analysant ces données à l'aide du MMC, les traders peuvent déduire les états cachés du marché et concevoir des stratégies de trading pour exploiter les opportunités potentielles.

Processus autorégressifs (PA)

Dans ces processus, la valeur à un moment donné dépend linéairement des valeurs précédentes.

Exemple

Utilisé dans les prévisions de séries temporelles pour prédire les valeurs futures de variables financières sur la base de leurs valeurs passées, ce qui facilite la formulation de stratégies d'investissement.

Processus de moyenne mobile (MM)

Ici, la valeur à un moment donné est une combinaison linéaire des termes d'erreur du bruit blanc passé.

Exemple

Utilisé dans l'analyse des séries chronologiques financières pour lisser les fluctuations à court terme et mettre en évidence les tendances ou les cycles à plus long terme.

Elle peut contribuer à la gestion des risques et à l'élaboration de stratégies.

Comment résoudre les équations différentielles stochastiques (EDS)

La résolution d'équations différentielles stochastiques (EDS) est une tâche de la finance quantitative, en particulier pour la modélisation des prix des actifs, des taux d'intérêt et d'autres variables financières.

Ces équations intègrent des variables aléatoires pour représenter les inconnues inhérentes aux marchés financiers.

Comprendre les EDD

Une EDD peut généralement être représentée sous la forme suivante:

dX = a(X, t) dt + b(X,t) dW

Où :

• X est le processus stochastique qui nous intéresse

• a(X, t) est le terme de dérive - par exemple, les rendements annuels des actions par an

• b(X,t) est le terme de diffusion - par exemple, le mouvement autour du rendement moyen de l'action

• dW représente un processus de Wiener ou un mouvement brownien.

Solutions analytiques

EDD linéaires

Certaines EDD peuvent être résolues analytiquement, en particulier les EDD linéaires comme le processus d'Ornstein-Uhlenbeck ou le mouvement brownien géométrique (MBG), qui est utilisé dans le modèle Black-Scholes.

Par exemple, l'EDD du MBG est donné par :

dSt= μ St dt + σ St dWt

Où :

• St est le prix de l'actif

• μ est le taux de dérive, et

• σ est la volatilité

• Wt est un processus de Wiener ou un mouvement brownien.

Techniques de transformation

Il est parfois possible de transformer une EDD en une forme plus simple qui peut être résolue analytiquement.

Cela implique souvent l'utilisation de méthodes telles que le lemme d'Ito pour manipuler l'EDD sous une forme reconnaissable.

Solutions numériques

Pour la plupart des scénarios pratiques en finance, les EDD n'ont pas de solutions de forme fermée et doivent être résolues numériquement.

Méthode d'Euler-Maruyama

Il s'agit d'une extension directe de la méthode d'Euler pour les équations différentielles ordinaires.

Elle permet d'obtenir une approximation de la solution à des pas de temps discrets.

La forme générale d'une EDS est approximée comme suit :

ΔX = Xt + a(Xt,t)Δt + b(Xt,t)ΔWt

Où ΔWt est l'incrément du processus de Wiener, qui peut être simulé comme une variable aléatoire normale de moyenne 0 et de variance Δt.

Méthode de Milstein

Cette méthode fournit une meilleure approximation que la méthode d'Euler-Maruyama en incluant un terme supplémentaire impliquant la dérivée du coefficient de diffusion.

Elle est particulièrement utile lorsque le terme de diffusion n'est pas linéaire.

Méthodes de Runge-Kutta (pour les EDD)

Il s'agit de méthodes d'ordre supérieur qui offrent une plus grande précision au prix d'une plus grande complexité de calcul.

Simulations de Monte Carlo

Il s'agit de simuler un grand nombre de trajectoires pour le processus stochastique et de calculer la moyenne des résultats.

Cette méthode est particulièrement utile pour l'évaluation de produits dérivés complexes ou pour les simulations de portefeuille.

Elle construit une distribution comme la suivante et permet d'effectuer des calculs tels que la VaR et d'autres mesures de risque :

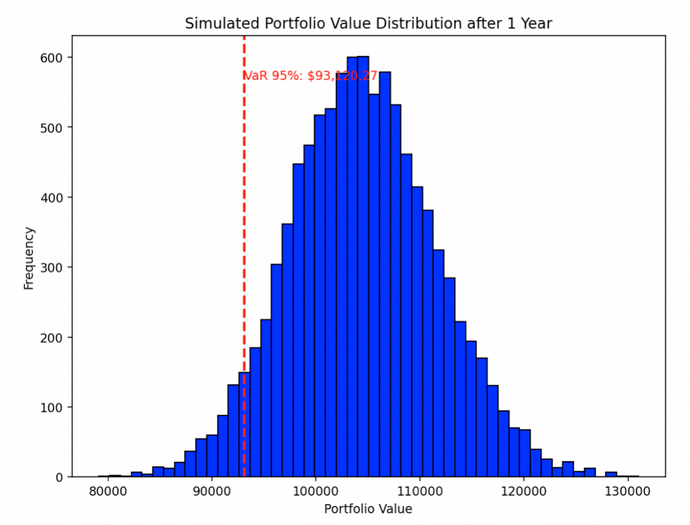
Considérations relatives à la mise en œuvre

Choix des pas de temps

La précision de la solution numérique dépend fortement du choix des pas de temps.

Des pas de temps plus petits augmentent la précision mais aussi le coût de calcul.

Génération de nombres aléatoires

La qualité du générateur de nombres aléatoires est importante, en particulier pour les simulations de Monte Carlo.

Stabilité et convergence

Assurez-vous que la méthode numérique est stable et qu'elle converge vers la vraie solution à mesure que le pas de temps diminue.

Langages de programmation

Python, avec des bibliothèques comme NumPy et SciPy, est couramment utilisé pour le prototypage en raison de sa facilité d'utilisation. (Des packages Python tels que SymPy et SDEPy sont également couramment utilisés pour résoudre les EDD).

Pour les tâches exigeant des performances élevées, il est préférable d'utiliser C++ ou Scala.

Résumé

Le choix de la méthode de résolution d'une EDD dépend de l'équation spécifique et du contexte dans lequel elle est utilisée.

Les solutions analytiques sont préférées pour leur précision, mais les solutions numériques sont plus polyvalentes et largement applicables dans les scénarios complexes du monde réel de la finance.

Processus stochastiques et calcul stochastique - Exemples Python (Estimation du prix des actions)

Les processus stochastiques et le calcul stochastique sont fondamentaux pour modéliser le comportement aléatoire des prix des actifs.

Nous allons fournir quelques exemples de codage.

Comme mentionné ci-dessus, l'un des modèles les plus utilisés pour la dynamique des prix des actions est le mouvement brownien géométrique (MBG), qui est un processus stochastique à temps continu.

Le MBG est utilisé dans le modèle Black-Scholes, entre autres, pour l'évaluation des options.

Voici un aperçu simplifié de la manière dont le prix d'une action peut être modélisé à l'aide du MBG :

Mouvement brownien géométrique (MBG)

Le GBM suppose que le logarithme du prix de l'action suit un mouvement brownien avec dérive.

Il est défini par l'équation différentielle stochastique (EDS) :

dSt= μ St dt + σ St dWt

Où :

• St est le prix de l'actif

• μ est le taux de dérive, et

• σ est la volatilité

• Wt est un processus de Wiener ou un mouvement brownien.

Voici comment vous pourriez estimer le prix d'une action un an à l'avance à l'aide de Python, en supposant un mouvement brownien géométrique :

import numpy as np

# Parameters
S0 = 100 # initial stock price
mu = 0.05 # expected return
sigma = 0.2 # volatility
T = 1.0 # time period in years
dt = 1/252 # time step size (assuming 252 trading days)
N = int(T/dt) # total # of time steps

# Generate random Brownian Motion
np.random.seed(97) 
dW = np.random.normal(0, np.sqrt(dt), N) # increments
W = np.cumsum(dW) # cumulative sum

# Simulate stock price path
St = S0 * np.exp((mu - 0.5 * sigma**2) * np.linspace(0, T, N) + sigma * W)

# Estimated stock price at end of period
S_T = St[-1]

print("Estimated stock price after one year: {:.2f}".format(S_T))

Dans cette simulation particulière, nous avons obtenu un prix de l'action de 84,62 à la fin d'une année (donc légèrement malchanceux par rapport à notre prix de départ de 100).

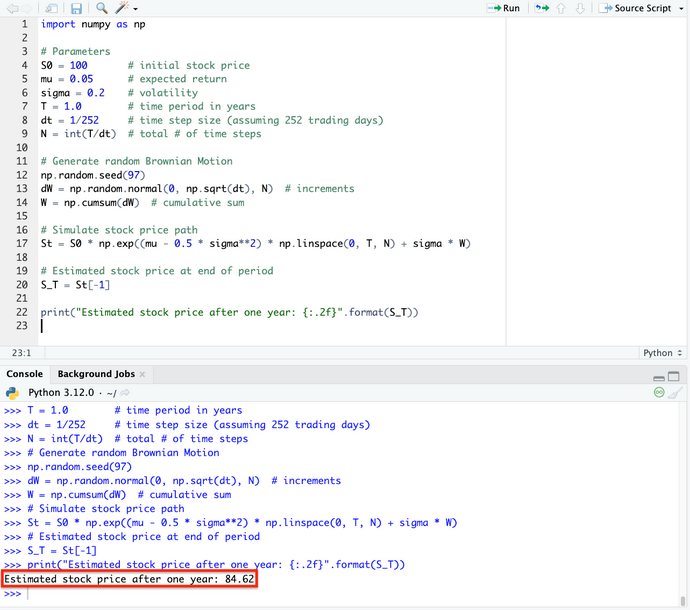
Points importants

• Utilisation pratique : Dans la réalité, vous utiliseriez des données historiques pour estimer les paramètres μ et σ d'une action particulière.

• Limites : Le modèle MBG suppose une dérive et une volatilité constantes, ce qui peut ne pas être le cas sur les marchés réels. Des modèles plus complexes, tels que les modèles de volatilité stochastique ou les modèles de diffusion par saut, peuvent être utilisés pour obtenir des scénarios plus précis ou plus réalistes.

• Risque et incertitude : il est essentiel de comprendre les hypothèses et les limites avant de l'utiliser pour prendre des décisions réelles de trading ou d'investissement.

Simulation (méthode Euler-Maruyama)

La méthode Euler-Maruyama est une technique numérique utilisée pour résoudre des équations différentielles stochastiques (EDS) telles que l'équation du mouvement brownien géométrique (MBG) pour les cours boursiers.

Il s'agit essentiellement de l'équivalent stochastique de la méthode d'Euler pour les équations différentielles ordinaires, adaptée pour traiter la composante aléatoire introduite par le mouvement brownien.

Cela implique la discrétisation du temps en petits intervalles et la mise à jour itérative du prix.

Voici comment implémenter la méthode Euler-Maruyama en Python pour estimer le prix futur de l'action à l'aide de MBG:

1. Discrétiser l'intervalle de temps en petits incréments.

2. Mettre à jour itérativement le prix de l'action en utilisant la formule GBM à chaque pas de temps.

L'équation différentielle stochastique pour GBM est la suivante :

dSt= μ St dt + σ St dWt

Pour simuler cela à l'aide de la méthode Euler-Maruyama, vous le discrétisez comme suit :

S(t+Δt) = St + μStΔt + σSt(√Δt)Zt

Ici, Zt est une variable aléatoire issue de la distribution normale standard, représentant l'incrément du processus de Wiener.

Voici donc le code Python utilisant Euler-Maruyama pour l'estimation du cours des actions à un an :

import numpy as np

# Parameters
S0 = 100 # initial stock price
mu = 0.05 # drift coefficient
sigma = 0.2 # volatility
T = 1.0 # time to maturity
dt = 1/252 # time step size (assuming 252 trading days)
N = int(T/dt) # number of time steps

# Random seed (do same as above)
np.random.seed(97)

# Initialize the stock price array
S = np.zeros(N)
S[0] = S0

# Simulate the stock price path
for t in range(1, N):
Z = np.random.normal() # random normal variable
S[t] = S[t-1] + mu * S[t-1] * dt + sigma * S[t-1] * np.sqrt(dt) * Z

# Estimated stock price at the end of the period
S_T = S[-1]

print(f"Estimated stock price after one year using Euler-Maruyama: {S_T:.2f}")

Cette méthode nous permet d'obtenir 86,06 :

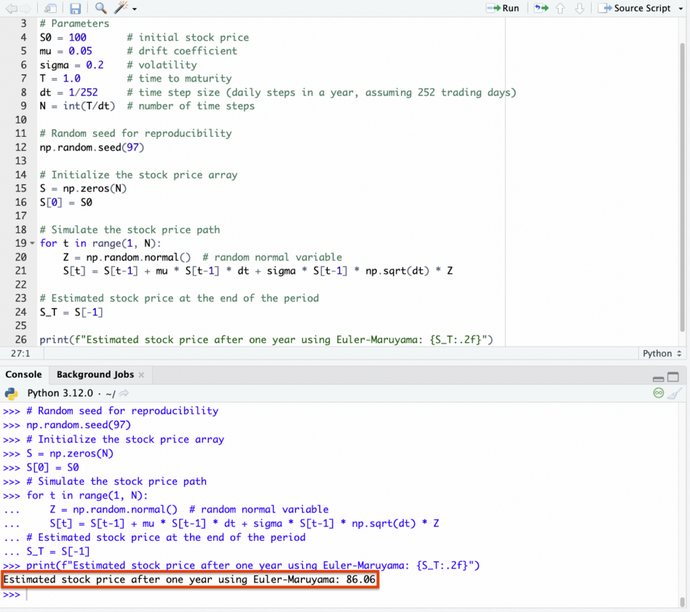
Points importants

Comme nous l'avons fait dans la section précédente :

• Précision : La précision de la méthode Euler-Maruyama dépend de la taille du pas de temps Δt. Des pas de temps plus petits conduisent généralement à des simulations plus précises mais nécessitent plus de calculs.

• Paramètres : Dans la pratique, vous estimerez μ (dérive) et σ (volatilité) à partir des données historiques de l'action.

• Risques et limites : Comme tous les modèles, il s'agit d'une simplification de la réalité. Les cours réels des actions peuvent présenter des sauts, un retour à la moyenne ou une volatilité stochastique. ou une volatilité stochastique, qui ne sont pas pris en compte par le simple modèle MBG. Il convient de toujours tenir compte des hypothèses et des limites du modèle lorsqu'il s'agit de prendre des décisions de trading dans le monde réel.

Conclusion

Ces processus servent d'outils fondamentaux dans l'analyse et la modélisation des séries temporelles financières et de divers phénomènes sur les marchés financiers.

Ils aident à la gestion du risque, à l'évaluation des options, à la formulation de stratégies de trading et d'investissement, etc.

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.