#1 24-01-2024 21:40:02

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 093

Distributions de probabilités en finance, marchés et trading

Les distributions de probabilités sont l'un des concepts les plus fondamentaux de la finance, des marchés et du trading.

Elles fournissent un cadre fondamental pour comprendre, modéliser et gérer les inconnues et les risques inhérents à ces domaines.

Le trading ne consiste pas tant à "prédire l'avenir" (c'est-à-dire à essayer d'établir une ligne déterministe sur la façon dont les choses vont se dérouler) qu'à reconnaître la nature probabiliste de l'exercice, où les résultats futurs peuvent être modélisés sous forme de distributions de probabilités.

L'éventail des inconnues est élevé par rapport à l'éventail des connaissances par rapport à ce qui est escompté dans le prix.

Un biais psychologique populaire, en général, est de vouloir naturellement penser de manière plus déterministe avec des heuristiques simples, plutôt que de manière plus nuancée en reconnaissant qu'un large éventail de résultats est possible.

Beaucoup de choses sont possibles, mais avec des probabilités très différentes, ce qui est la nature des distributions de probabilités.

Dans le domaine du trading et des marchés, nous avons tendance à être influencés par nos propres expériences et par les expériences récentes, et à sous-estimer la probabilité d'événements "extrêmes" qui diffèrent des événements récents.

Principaux enseignements:

Modélisation - Les distributions de probabilités sont utilisées pour montrer l'éventail des résultats possibles et les probabilités estimées/actualisées (ou parfois connues) associées à chacun d'entre eux.

Comprendre le risque - Les distributions de probabilités, en particulier le comportement de la queue, sont importantes pour évaluer les risques de marché et les événements extrêmes.

Optimiser les portefeuilles - Les moments tels que la moyenne et la variance sont les plus fondamentaux. Ils sont couramment utilisés pour la diversification des portefeuilles et l'optimisation du rapport risque/rendement.

Fixer le prix des produits dérivés - Les moments d'ordre supérieur (asymétrie, aplatissement) influencent la fixation du prix des options et la volatilité implicite.

• Les moments d'ordre supérieur et les cumulants permettent une représentation plus précise et plus nuancée de la distribution du rendement attendu de l'actif sous-jacent.

• Leur inclusion dans les modèles d'évaluation aide à saisir les risques associés aux mouvements extrêmes du marché, ce qui est essentiel pour les options. Les gains des options (en particulier) peuvent être très sensibles à ces mouvements.

Identifier les anomalies du marché - Les moments peuvent donner un aperçu des inefficacités du marché et du comportement des traders/investisseurs.

Prise de décision éclairée - La connaissance des distributions et des moments permet de prendre des décisions de trading plus objectives.

Schéma conceptuel pour comprendre les moments

• Moyenne (1er moment) - Tendance centrale ou niveau moyen.

• Variance (2e moment) - Écart ou écart moyen au carré par rapport à la moyenne.

• Asymétrie (3ème moment) - Asymétrie ou biais dans une direction.

• Aplatissement (4e moment) - Asymétrie ou propension aux valeurs extrêmes..

• Cinquième moment et au-delà - Aspects de plus en plus complexes de la forme de la distribution, en particulier dans les queues et les extrémités.

Les bases des distributions de probabilités dans la finance, les marchés et le trading

Les distributions de probabilités en finance, marchés et trading sont des fonctions mathématiques qui représentent la probabilité de différents résultats ou rendements d'un investissement ou d'une transaction.

Elles facilitent l'évaluation des risques et la prise de décision en quantifiant les inconnues et les variations potentielles dans les comportements du marché ou les performances des actifs financiers.

Distributions de probabilités et évolution temporelle

L'évolution temporelle des distributions de probabilité en finance montre qu'au fil du temps, l'éventail et la forme des résultats potentiels des rendements des actifs ou des comportements du marché peuvent changer, ce qui indique une évolution des risques, des résultats potentiels et des inconnues.

Cela nécessite des ajustements dynamiques et continus dans l'évaluation des risques et les stratégies de négociation et d'investissement.

Exemple non financier

Supposons que vous traciez les fourchettes de taille et de poids des personnes en fonction de leur âge, de leur sexe, de leur lieu de résidence et d'autres données.

Par exemple, si vous voulez prédire la taille d'un Américain, vous savez qu'il est plus probable qu'il mesure 1,80 m que 1,80 m ou 1,80 m, et que son poids est plus probable qu'il pèse 1,80 m que 1,80 m ou 1,80 m. Mais il peut se situer n'importe où dans cette fourchette.

Mais il pourrait se situer n'importe où dans cette fourchette (ou même en dehors de cette fourchette), mais avec des probabilités très variables au sein d'un vaste ensemble de possibilités.

Il y a aussi la nature de la distribution.

• Les valeurs aberrantes sont-elles plus fréquentes (avons-nous des queues plus larges ou plus d'aplatissement) ?

• Quelle est l'asymétrie de la distribution ? Si la moyenne est de 1,80 m, la population est-elle répartie uniformément de chaque côté ou les personnes plus grandes ou plus petites sont-elles plus fréquentes ? Et ainsi de suite.

• Quelles sont les variables qui influencent la distribution ?

• Comment la répartition évolue-t-elle dans le temps ?

• En quoi est-elle différente pour d'autres régions, sous-régions ou d'autres données démographiques ?

S'il existait un marché sur lequel il était possible de parier, nous devrions recueillir autant d'informations que possible pour déterminer la nature de la distribution, la comparer à la distribution actualisée par le marché (sur la base des paris réels effectués sur les marchés concernés) et l'utiliser pour faire nos propres paris (si possible) qui fournissent une valeur attendue positive.

Voici un aperçu de l'importance des distributions de probabilités dans différentes catégories :

Évaluation et gestion des risques

Comprendre les rendements des actifs

Les distributions de probabilités permettent de modéliser les rendements de différents actifs financiers.

En comprenant la distribution des rendements, les traders peuvent mieux connaître le risque et les bénéfices potentiels associés à un actif.

Par exemple, si nous voulons une distribution de probabilité du rendement du SPY à plus de deux ans, nous constatons une large distribution de résultats potentiels :

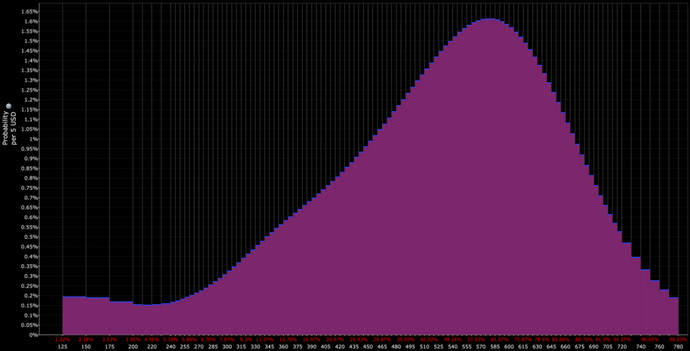
Risque de queue

Les distributions avec des queues lourdes mettent en évidence le potentiel d'événements extrêmes (événements "cygne noir") ou simplement d'événements qui se produiraient plus souvent qu'on ne le pense.

Cela permet de se préparer à des mouvements de marché peu probables mais potentiellement dévastateurs.

Construction du portefeuille

Diversification

En comprenant les distributions conjointes des rendements des actifs, les traders/investisseurs peuvent construire des portefeuilles qui optimisent le couple risque-rendement.

Corrélation et covariances

Il s'agit d'évaluer les corrélations et les covariances, qui sont dérivées des distributions de probabilité conjointes des rendements des actifs OU en comprenant leurs caractéristiques fondamentales et en ne se basant pas simplement sur des données passées (qui peuvent ne pas représenter l'avenir).

Frontière efficiente

Le concept de frontière efficiente dans la théorie du portefeuille, qui représente l'ensemble des portefeuilles optimaux offrant le meilleur rendement attendu possible pour un niveau de risque donné, est basé sur la distribution de probabilité des rendements.

Dans la finance quantitative moderne, l'optimisation de la moyenne-variance est un cadre trop simpliste, mais l'idée générale (être compensé pour le risque, diversification pour améliorer les rendements ajustés au risque) reste vraie.

De nombreuses mesures courantes de rendement ajusté au risque sont basées sur les deux premiers moments de la distribution ou sur des variations de celle-ci (par exemple, Sharpe, Sortino).

Évaluation des produits dérivés

Modèles d'évaluation des options

Les modèles comme celui de Black-Scholes utilisent des distributions de probabilités (généralement normales ou log-normales) pour fixer le prix des options.

Ces modèles intègrent la distribution des prix futurs potentiels de l'actif sous-jacent pour calculer la juste valeur des options.

Volatilité implicite

Le concept de volatilité implicite, qui est un élément important dans la détermination du prix des options, est dérivé de l'opinion consensuelle du marché sur la distribution future des prix des actifs.

Analyse du comportement des marchés

Finance comportementale

Les distributions de probabilités sont utilisées pour étudier les anomalies du marché et le comportement des traders/investisseurs.

Par exemple, les distributions qui capturent l'asymétrie et l'aplatissement peuvent expliquer pourquoi les investisseurs peuvent avoir des préférences pour les actifs dont les gains sont de type "loterie" (convexes).

Modèles de prédiction du marché

Les modèles statistiques et les algorithmes d'apprentissage automatique s'appuient souvent sur des distributions de probabilités pour prédire les mouvements du marché et identifier les opportunités de trading.

Mesure de la performance ajustée au risque et trading algorithmique

Mesure de la performance

Des mesures telles que le ratio de Sharpe, le ratio de Sortino et la valeur à risque (VaR) s'appuient sur la distribution des rendements des actifs pour mesurer la performance ajustée au risque des transactions ou des investissements.

Tests de stress

Les institutions financières utilisent les distributions de probabilité dans les tests de résistance et l'analyse de scénarios pour évaluer la performance des portefeuilles dans diverses conditions de marché défavorables.

Stratégies quantitatives

De nombreuses stratégies de trading algorithmique sont basées sur des modèles statistiques qui supposent des distributions de probabilité spécifiques pour les prix et les rendements des actifs - ou du moins utilisent ces formes fonctionnelles pour le prototypage des algorithmes en cours de développement.

Par exemple, dans un grand nombre de nos articles, nous réalisons généralement des prototypes en Python en utilisant des distributions normales lorsque nous montrons un exemple conceptuel.

Les modèles mathématiques sont utilisés pour identifier des modèles et exécuter des transactions.

Contrôle du risque

Le trading algorithmique utilise également des distributions de probabilités pour fixer des limites et des paramètres de risque.

Cela permet de s'assurer que les stratégies de trading automatisées fonctionnent dans des limites de risque acceptables.

Moyenne et variance

Dans les distributions de probabilités, la moyenne et la variance sont deux concepts fondamentaux qui décrivent les principales caractéristiques de la distribution.

Moyenne

La moyenne, souvent appelée valeur attendue ou moyenne, est une mesure de la tendance centrale d'une distribution.

Elle est calculée comme la somme de toutes les valeurs possibles pondérées par leurs probabilités respectives.

En termes simples, elle représente le résultat moyen si une expérience ou un processus était répété plusieurs fois.

Par exemple, dans un lancer de dés, la valeur moyenne est de 3,5, ce qui représente le résultat moyen d'un lancer de dés répété.

De même, dans un système fermé tel que le lancer de deux dés, nous connaissons la distribution de probabilité associée.

Variance

La variance mesure l'étendue ou la dispersion de la distribution autour de la moyenne.

Elle est calculée comme la moyenne des différences au carré par rapport à la moyenne, ce qui donne une idée de l'écart entre les valeurs individuelles de la distribution et la moyenne.

Une variance élevée indique que les points de données sont répartis sur un large éventail de valeurs, tandis qu'une variance faible indique qu'ils sont étroitement regroupés autour de la moyenne.

Par exemple, dans une distribution où toutes les valeurs sont identiques, la variance est nulle, car il n'y a pas d'écart par rapport à la moyenne.

Ensemble, la moyenne et la variance fournissent une description basique mais généralement solide du comportement d'une distribution de probabilités en indiquant à la fois sa tendance centrale et la variabilité des résultats.

Termes similaires à Moyenne et variance

De nombreux termes analogues en finance sont utilisés de manière interchangeable ou presque avec la moyenne et la variance.

Il s'agit par exemple du rendement (moyenne) et de la volatilité ou du risque (variance).

L'asymétrie et l'aplatissement

L'asymétrie et l'aplatissement sont des "moments supérieurs" utilisés pour décrire une distribution de probabilité.

Asymétrie (Skew)

En finance, l'asymétrie fait référence à l'asymétrie de la distribution des rendements des actifs.

Elle indique une tendance des rendements à pencher davantage d'un côté de la moyenne.

Une asymétrie positive implique des petites pertes plus fréquentes et des gains importants occasionnels, tandis qu'une asymétrie négative indique des petits gains fréquents et des pertes importantes rares.

Aplatissement (kurtosis)

L'aplatissement mesure la "queue" de la distribution des rendements.

Un aplatissement élevé indique une probabilité plus élevée de rendements extrêmes (très élevés ou très faibles) par rapport à une distribution normale.

Cela augmente le risque potentiel et l'imprévisibilité d'un investissement.

Optimisation de l'asymétrie et de l'aplatissement

Outre l'optimisation de la moyenne (aussi élevée que possible) et de la variance (aussi faible que possible), l'optimisation de l'asymétrie et de l'aplatissement vise à obtenir une asymétrie aussi positive que possible (plus de chances d'obtenir des rendements élevés) et un aplatissement faible (pour minimiser les risques de queue de distribution).

Par exemple, si nous reprenons la distribution présentée plus haut dans l'article, celle-ci présente une asymétrie positive et une aplatissement élevé.

Ces caractéristiques sont logiques, puisqu'il s'agit du SPY (ETF de l'indice S&P 500), où les actions ont un rendement attendu positif (une "dérive" positive) et des queues plus larges par rapport à ce que prévoirait une distribution normale.

La distribution normale se caractérise par une asymétrie et une aplatissement nuls.

Moments d'ordre supérieur et autres concepts dans les distributions de probabilité

Dans les distributions de probabilités financières, les moments au-delà de ceux que nous avons référencés (moyenne, variance, asymétrie et aplatissement) deviennent de plus en plus complexes et abstraits.

Néanmoins, ils peuvent fournir des informations plus approfondies sur le comportement des variables financières.

Voici quelques moments supplémentaires et des concepts connexes :

Moments d'ordre supérieur

Il s'agit des moments 5, 6 et plus d'une distribution.

Bien que leur interprétation pratique soit moins intuitive que celle des quatre premiers moments, ils permettent de saisir des aspects plus détaillés de la forme de la distribution, en particulier dans les queues.

Cumulants

Les cumulants sont apparentés aux moments mais possèdent certaines propriétés avantageuses.

Les quatre premiers cumulants sont identiques aux quatre premiers moments (moyenne, variance, asymétrie, aplatissement).

Mais les cumulants d'ordre supérieur peuvent donner un aperçu différent de la structure de la distribution, principalement en termes de dépendances et de relations entre les variables.

Moments centraux

Il s'agit des moments autour de la moyenne de la distribution.

Alors que le premier moment central est toujours nul, les moments centraux supérieurs peuvent fournir des informations sur la forme de la distribution par rapport à sa moyenne.

Moments L

Les moments L sont des combinaisons linéaires de statistiques d'ordre.

Ils sont utiles dans l'analyse des données avec des queues lourdes ou des valeurs aberrantes.

Les moments L sont souvent utilisés pour une estimation plus robuste des paramètres de distribution que les moments conventionnels.

Fonctions génératrices de moments

Bien qu'il ne s'agisse pas techniquement d'un moment, la fonction génératrice de moments (FGM) d'une distribution peut être utilisée pour trouver tous les moments de la distribution.

La nième dérivée de la FGM, évaluée à zéro, donne le nième moment.

Fonction caractéristique

Comme la FGM, la fonction caractéristique peut être utilisée pour dériver tous les moments d'une distribution de probabilité.

Elle est utile pour les distributions pour lesquelles il n'existe pas de FGM.

Entropie

Dans le contexte de la théorie de l'information, l'entropie mesure l'incertitude ou le caractère aléatoire d'une distribution.

Il ne s'agit pas d'un moment au sens traditionnel du terme, mais d'une perspective différente sur les caractéristiques de la distribution.

Co-squewness et Co-kurtosis

Il s'agit de mesures de l'évolution d'une variable aléatoire par rapport à l'asymétrie et à l'aplatissement d'une autre variable aléatoire.

Elles sont importantes dans la théorie des portefeuilles pour comprendre le comportement conjoint des rendements des actifs.

Dépendance de la queue

Bien qu'il ne s'agisse pas d'un moment, la dépendance de queue est un concept de la gestion des risques financiers.

Elle mesure la probabilité que des mouvements extrêmes d'une variable se produisent simultanément avec des mouvements extrêmes d'une autre variable.

Moments conditionnels

Il s'agit de moments calculés sous certaines conditions ou hypothèses. La variance conditionnelle est un concept clé dans la modélisation de la volatilité.

Moments officiels

L'étiquetage et la conceptualisation des moments d'ordre supérieur au-delà du quatrième moment (kurtosis) peuvent s'avérer difficiles, car leurs interprétations pratiques sont moins intuitives et plus abstraites.

Nous pouvons néanmoins les étiqueter et fournir une carte généralisée pour conceptualiser ces moments :

Premier moment - Moyenne

Il s'agit de la valeur moyenne de la distribution.

Il fournit la position centrale ou la valeur attendue de la distribution.

Deuxième moment - Variance

Elle mesure la dispersion ou l'étendue de la distribution autour de la moyenne.

Il s'agit d'une mesure de la largeur de la distribution qui donne une idée de l'écart typique des valeurs individuelles par rapport à la moyenne.

Troisième moment - Asymétrie

L'asymétrie indique l'asymétrie de la distribution.

Une asymétrie positive signifie que la queue est plus longue ou plus grosse du côté droit.

Une asymétrie négative signifie que la queue est plus longue ou plus grosse à gauche.

Quatrième moment - Kurtosis

Il s'agit d'une mesure de la "queue" de la distribution.

Un kurtosis élevé indique des queues lourdes et un pic prononcé (leptokurtique).

Un kurtosis faible indique des queues légères et un pic plat (platykurtique).

Cinquième moment et au-delà

Les moments d'ordre supérieur (5e, 6e, etc.) continuent à décrire des caractéristiques de plus en plus complexes et subtiles de la forme de la distribution, principalement dans les queues.

Cinquième moment

Mesure l'asymétrie des queues.

Contrairement à l'asymétrie, qui mesure l'asymétrie dans une direction, le cinquième moment la saisit d'une manière plus complexe.

Sixième moment et plus

Ces moments permettent de saisir des détails de plus en plus fins sur la forme de la distribution, en particulier les extrémités et les bizarreries des queues.

Applications des moments d'ordre 5 et au-delà

Les quatre premiers moments ont des interprétations claires et largement acceptées, mais les moments plus élevés deviennent progressivement plus abstraits et moins intuitifs.

En analyse financière, les moments au-delà du quatrième sont rarement utilisés en raison de la difficulté de leur estimation et de leur interprétation.

Leur utilité pratique réside souvent dans des contextes théoriques spécifiques ou dans la modélisation statistique et quantitative avancée.

Cumulants

Discuter des cumulants d'ordre supérieur implique d'aborder des aspects plus complexes de la caractérisation des distributions statistiques.

Les cumulants, comme les moments, sont un ensemble de statistiques qui décrivent diverses caractéristiques d'une distribution de probabilité.

Alors que les premier et deuxième cumulants correspondent respectivement à la moyenne et à la variance, les cumulants d'ordre supérieur permettent de mieux comprendre la forme de la distribution, en particulier son asymétrie et le comportement de sa queue.

Cumulants d'ordre supérieur

Troisième cumul (équivalent à l'asymétrie)

• Décrit l'asymétrie d'une distribution.

• Une valeur positive du troisième cumulant indique que la queue de la distribution est plus longue ou plus lourde du côté droit, tandis qu'une valeur négative indique que la queue est plus longue ou plus lourde du côté gauche.

• En finance, une asymétrie positive est souvent préférée car elle suggère une plus grande probabilité de rendements positifs extrêmes.

Quatrième cumul (excès de kurtosis)

• Mesure la "queue" ou la propension aux résultats extrêmes d'une distribution.

• Un quatrième cumulant plus élevé indique une distribution avec des queues plus lourdes et un pic plus net par rapport à une distribution normale.

• En termes financiers, un kurtosis élevé implique un risque plus élevé de mouvements extrêmes du marché, à la hausse comme à la baisse.

Cinquième cumul et au-delà

• Ces cumulants saisissent des aspects de plus en plus complexes de la forme de la distribution dans les queues.

• Le cinquième cumulant peut fournir des indications sur l'asymétrie des queues, différente de l'asymétrie capturée par le troisième cumulant.

• Les cumulants supérieurs (sixième, septième, etc.) sont plus difficiles à interpréter et sont moins couramment utilisés, mais ils continuent à décrire des caractéristiques plus fines et plus subtiles de la distribution (comme les nuances dans la forme de ses queues).

Importance en probabilités et en finance

Théorie des probabilités

En théorie des probabilités, les cumulants d'ordre supérieur sont importants pour comprendre la structure détaillée des distributions de probabilité, en particulier dans le contexte de la modélisation statistique avancée et des études théoriques.

Alors que les premiers cumulants (moyenne, variance, asymétrie, aplatissement) sont largement utilisés et compris, les cumulants d'ordre supérieur jouent un rôle plus spécialisé dans les statistiques et la finance (principalement dans les situations où le risque de queue et les événements extrêmes sont particulièrement préoccupants).

La finance

En finance, les cumulants d'ordre supérieur sont très importants dans les domaines de la gestion des risques et de l'évaluation des produits dérivés.

Ils fournissent des informations sur la probabilité et l'impact des mouvements extrêmes du marché, ce qui est important pour l'évaluation des options et d'autres produits financiers dérivés.

Par exemple, les modèles d'évaluation des options, tels que ceux utilisés dans l'évaluation des options exotiques, peuvent nécessiter une compréhension des cumulants d'ordre supérieur afin de capturer avec précision le risque de mouvements importants du marché.

D'autres quants peuvent étudier les moments/cumulants d'ordre supérieur pour obtenir un avantage commercial d'une manière ou d'une autre.

Défis pratiques

Les cumulants d'ordre supérieur sont de plus en plus difficiles à estimer avec précision à partir de données empiriques.

Par conséquent, leur utilisation pratique est souvent limitée à des études théoriques ou à des contextes spécifiques où la caractérisation précise des queues de distribution est essentielle.

Moments et cumulants

Les moments et les cumulants sont deux façons différentes mais apparentées de décrire les caractéristiques d'une distribution de probabilités.

Les moments constituent un moyen direct et intuitif de comprendre les caractéristiques d'une distribution.

Les cumulants offrent une vision plus nuancée, en particulier pour l'analyse des risques de queue et des événements extrêmes en finance.

Les moments sont généralement plus couramment utilisés pour l'analyse financière de base, mais les cumulants deviennent importants dans les domaines plus complexes de la finance quantitative.

Les comprendre dans le contexte de la finance peut s'avérer très utile, en particulier lors de l'analyse des profils de risque et de rendement des actifs/investissements/instruments/opérations.

Voici une explication simple (et un petit rappel de ce qui précède) :

Moments

Ce qu'ils sont

Les moments sont des mesures quantitatives liées à la forme de la fonction de densité de probabilité d'une distribution.

Ils comprennent la moyenne (premier moment), la variance (deuxième moment), l'asymétrie (troisième moment) et l'aplatissement (quatrième moment), entre autres.

Types

Le premier moment est la moyenne, le deuxième est la variance (étendue de la distribution), le troisième est l'asymétrie (skewness) et le quatrième est l'aplatissement (kurtosis).

En finance

Les moments sont utiles pour évaluer les risques et les rendements des investissements.

Par exemple, la moyenne (premier moment) indique le rendement attendu d'un actif financier, tandis que la variance (deuxième moment) mesure la volatilité ou le risque de l'actif.

L'asymétrie (troisième moment) et l'aplatissement (quatrième moment) sont importants lorsqu'il s'agit d'évaluer la probabilité de rendements extrêmes ou d'événements de type "cygne noir".

Cumulants

Ce qu'ils sont

Les cumulants, comme les moments, permettent de décrire une distribution, mais ils se concentrent davantage sur la structure de la distribution en termes de pic central et de queues.

Les cumulants sont dérivés du logarithme de la fonction caractéristique d'une distribution, où les premiers cumulants correspondent à la moyenne, à la variance, à l'asymétrie et à l'aplatissement, mais diffèrent dans les ordres supérieurs et fournissent une description plus nuancée des caractéristiques de la distribution.

Relation avec les moments

Les premier et deuxième cumulants correspondent aux deux premiers moments (moyenne et variance).

Les cumulants supérieurs (troisième, quatrième, etc.) ne sont pas aussi précisément égaux que les moments correspondants, mais fournissent des informations supplémentaires sur la forme de la distribution.

En finance

Les cumulants, en particulier ceux d'ordre supérieur, peuvent être utiles dans la modélisation financière et l'évaluation des risques, en particulier dans la tarification des produits dérivés complexes et la modélisation des risques.

Ils peuvent offrir une compréhension plus nuancée du comportement de la queue de la distribution à des fins de gestion du risque.

Exemples et relation avec la probabilité et la finance

• Moyenne (1er moment) / 1er cumul - Elle représente le rendement moyen d'un actif financier. Par exemple, si une action a un rendement annuel moyen de 8 %, la moyenne ou le premier moment/cumulant de sa distribution de rendement est de 8 %.

• Variance (2e moment) / 2e cumul - Elle mesure la variabilité ou le risque des rendements de l'actif. Une variance plus élevée indique un risque plus important. Si les rendements d'une action varient fortement d'une année à l'autre, sa variance est élevée.

• Skewness (3ème moment) - En finance, le skewness peut indiquer la tendance d'un actif à avoir des rendements asymétriques. Une asymétrie positive peut impliquer une plus grande probabilité de rendements exceptionnellement élevés, tandis qu'une asymétrie négative suggère un risque plus élevé de pertes substantielles.

• Kurtosis (4ème moment) - Un kurtosis élevé dans un actif financier indique un risque plus élevé de rendements extrêmes (à la fois positifs et négatifs). Par exemple, les actions ont souvent un kurtosis élevé en raison de leur potentiel de gains très élevés et de pertes substantielles.

• Cumulants d'ordre supérieur - Ils deviennent importants dans les modèles financiers avancés, tels que ceux utilisés dans l'évaluation des options, où le comportement de la queue des rendements des actifs peut avoir un impact significatif sur l'évaluation des produits financiers dérivés.

Cumulants pour les données paramétriques et non paramétriques

Les cumulants, y compris ceux d'ordre supérieur, peuvent être utilisés pour caractériser les distributions paramétriques et non paramétriques.

Leur application n'est pas limitée aux distributions avec des paramètres spécifiques.

Cela en fait des outils polyvalents pour l'analyse statistique et les applications pratiques/du monde réel.

Distributions paramétriques

Les distributions paramétriques sont celles qui sont entièrement décrites par un ensemble de paramètres.

Les exemples classiques sont la distribution normale, la distribution binomiale et la distribution de Poisson.

Les cumulants dans les distributions paramétriques

Pour ces distributions, les cumulants peuvent souvent être calculés explicitement sur la base des paramètres de la distribution.

Par exemple, dans une distribution normale, tous les cumulants au-delà du deuxième sont nuls, ce qui est une propriété distinctive de la distribution normale.

Distributions non paramétriques

Les distributions non paramétriques n'ont pas de forme fonctionnelle spécifique.

Elles sont souvent utilisées lorsque l'on dispose de peu de connaissances préalables sur la forme de la distribution ou lorsque les données ne s'intègrent pas bien dans les formes paramétriques courantes.

Cumul dans les distributions non paramétriques

Les cumulants peuvent être estimés à partir des données sans supposer de modèle de distribution spécifique.

Ils sont donc utiles dans les applications réelles où la distribution de probabilité sous-jacente est inconnue ou complexe.

Applications

En finance, par exemple, les distributions de rendement des actifs sont souvent non paramétriques, avec des caractéristiques telles que l'asymétrie et les queues lourdes qui ne sont pas bien prises en compte par les modèles paramétriques simples.

Les cumulants permettent de mieux comprendre ces distributions, ce qui est important pour la gestion des risques et l'évaluation des produits dérivés.

Considérations pratiques

Difficultés d'estimation

L'estimation des cumulants d'ordre supérieur dans les distributions non paramétriques peut s'avérer difficile.

Cela est particulièrement vrai pour les échantillons de taille limitée, car ces estimations peuvent devenir de plus en plus sensibles à l'erreur d'échantillonnage.

Interprétation

Les quatre premiers cumulants (moyenne, variance, asymétrie et aplatissement) ont des interprétations claires. Les cumulants d'ordre supérieur peuvent être plus difficiles à interpréter, en particulier dans le contexte des modèles non paramétriques.

Moments et cumulants d'ordre supérieur dans le contexte de l'évaluation des options

Dans le contexte de l'évaluation des options, les moments d'ordre supérieur et les cumulants saisissent les nuances des distributions des rendements des actifs, ce qui peut avoir des implications profondes sur l'évaluation des options.

Les options sont sensibles non seulement à la moyenne et à la variance des rendements de l'actif sous-jacent (comme le montrent les deux premiers moments/cumulants), mais aussi à la forme de la distribution des rendements, et c'est là que les moments d'ordre supérieur et les cumulants prennent toute leur importance.

Moments d'ordre supérieur dans l'évaluation des options

Skewness (3ème moment)

[*]Rôle - Le skewness détermine le degré d'asymétrie de la distribution des rendements, ce qui influe sur le prix des options hors de la monnaie (OTM).[/*]
[*]Impact - Un skewness positif indique une probabilité plus élevée de rendements extrêmement positifs, ce qui peut faire augmenter le prix des options d'achat OTM. Inversement, une asymétrie négative, indiquant une probabilité plus élevée de rendements extrêmement négatifs, peut faire augmenter le prix des options de vente OTM.[/*]

Kurtosis (4ème moment)

• Rôle - Le kurtosis mesure la "grosseur" des queues de la distribution. Un kurtosis élevé implique une probabilité plus élevée de rendements extrêmes, tant positifs que négatifs.

• Impact - Un kurtosis élevé augmente la valeur des options d'achat et de vente OTM, car il suggère une plus grande probabilité de mouvements de prix significatifs, à la hausse ou à la baisse.

Les cumulants d'ordre supérieur dans l'évaluation des options

Troisième et quatrième cumulants

• Ils sont étroitement liés à la skewness et à la kurtosis, respectivement, et influencent de la même manière l'évaluation des options en affectant l'évaluation des options OTM.

• Dans les modèles avancés d'évaluation des options, tels que ceux utilisés pour les options exotiques, la caractérisation précise du comportement de la queue de la distribution des rendements (tel que décrit par les cumulants d'ordre supérieur) peut être très importante.

Application pratique

Modèles standard

Les modèles traditionnels tels que le modèle Black-Scholes supposent une distribution normale des rendements (c'est-à-dire sans asymétrie ni excès d'aplatissement).

Malheureusement, cette hypothèse ne reflète pas toujours la réalité des marchés financiers, où les asymétries et les queues grasses sont la norme.

Modèles avancés

Pour remédier à ce problème, des modèles plus sophistiqués - par exemple, des modèles de volatilité stochastique ou des modèles de diffusion par saut - intègrent ces moments d'ordre supérieur.

Ces modèles sont mieux équipés pour traiter les marchés financiers réels, comme les sauts soudains dans les prix ou le smile de volatilité - une tendance observée dans la volatilité implicite des options pour différents prix d'exercice.

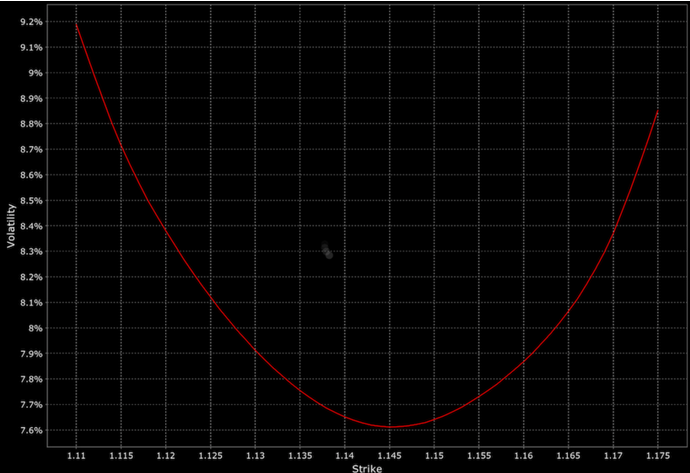
Implications

L'incorporation de moments et de cumulants d'ordre supérieur permet une évaluation plus précise des options, notamment dans les situations où des mouvements extrêmes du marché sont plus probables ou pendant les périodes de tensions sur le marché.

(Les options sont des instruments convexes et beaucoup plus sensibles aux mouvements extrêmes que l'actif sous-jacent).

Brokers d'options

Investir comporte des risques de perte

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.