#1 02-02-2024 14:41:44

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 299

L'analyse complexe et les nombres complexes dans la finance, le trading et l'investissement

L'analyse complexe est une branche des mathématiques qui se concentre sur les fonctions des nombres complexes.

Les nombres complexes, qui mélangent des parties réelles et imaginaires, sont importants car ils nous permettent de résoudre des équations (x^2 = -1) qui ne peuvent pas être résolues avec des nombres réels, ce qui élargit notre compréhension et nos capacités dans divers domaines (par exemple, la finance, l'apprentissage automatique, le trading quantique).

Principaux enseignements

Les nombres complexes

• Un nombre complexe combine un nombre réel et un nombre imaginaire.

• Il s'écrit généralement sous la forme a + bi, où a et b sont des nombres réels et i l'unité imaginaire.

• Les nombres complexes nous permettent d'explorer et de résoudre des équations et des problèmes que les nombres ordinaires ne peuvent pas résoudre (le carré d'une inconnue étant un nombre négatif) - en ajoutant une dimension supplémentaire qui ouvre de nouvelles voies pour comprendre le monde qui nous entoure.

Modélisation du comportement des prix

• L'analyse complexe, en particulier par le biais des transformées de Fourier, aide à décomposer les mouvements des prix des actifs.

• Elle permet de mieux prédire les prix futurs.

Tarification des options

• Utilisée dans des modèles avancés pour évaluer avec plus de précision les produits dérivés et les options complexes.

Gestion du risque

• Améliore l'évaluation du risque de portefeuille en saisissant les aspects multidimensionnels des instruments financiers et des conditions de marché.

Vous trouverez ci-dessous quelques concepts et applications clés dans ces domaines :

Concepts fondamentaux de l'analyse complexe

Les nombres complexes sont un type de nombre qui étend l'idée traditionnelle des nombres.

En termes simples, un nombre complexe est une combinaison d'un nombre réel et d'un nombre imaginaire.

Pour comprendre ce concept, décomposons-le :

Les nombres réels

Ce sont les nombres que nous utilisons dans la vie de tous les jours, comme 1, -3, 0,5, etc.

Ils peuvent être positifs, négatifs ou nuls.

Les nombres imaginaires

Un nombre imaginaire est défini par la racine carrée de -1, qui n'est pas un nombre réel (puisque la mise au carré de tout nombre réel donne toujours un résultat positif).

Cette racine carrée de -1 est représentée par le symbole i.

Nombres complexes

Nombres de la forme :

a + bi

Où :

• a et b sont des nombres réels, et

• i est l'unité imaginaire (x^2 = -1)

Par exemple, 3 + 4i est un nombre complexe, où 3 est la partie réelle et 4i la partie imaginaire.

Les nombres complexes élargissent notre compréhension des nombres et nous permettent de résoudre des équations qui ne peuvent être résolues en utilisant uniquement des nombres réels, comme la racine carrée d'un nombre négatif.

Ils sont utiles en mathématiques avancées, en physique, en ingénierie et dans certains domaines de la finance.

Fonctions analytiques

Les fonctions qui sont complexes et différentiables dans un voisinage de chaque point de leur domaine.

Cette différentiabilité conduit à des propriétés puissantes telles que la conformité et la capacité à se développer en séries de puissances.

• La conformité fait référence à la propriété des fonctions complexes différentiables de préserver localement les angles et les formes (mais pas nécessairement les tailles) des figures géométriques.

• La capacité à se développer en séries de puissances signifie que ces fonctions peuvent être représentées comme une somme de puissances de nombres complexes.

Intégration des contours

Intégrale d'une fonction complexe le long d'une trajectoire dans le plan complexe.

Elle est importante pour l'évaluation des intégrales en analyse réelle grâce à des techniques telles que le théorème des résidus.

Pourquoi les nombres imaginaires sont-ils importants en finance ?

La racine carrée de -1, représentée par i, est importante car elle nous permet de résoudre des problèmes mathématiques qu'il serait impossible de résoudre en utilisant uniquement des nombres réels.

Ce concept permet de réaliser plusieurs choses essentielles :

Résoudre des équations autrement impossibles - Sans i, nous ne pouvons pas trouver de solutions à des équations simples telles que x^2 = -1, car aucun nombre réel élevé au carré ne donne un résultat négatif. L'introduction de i nous permet de résoudre de telles équations.

En finance quantitative, les nombres complexes peuvent être importants pour résoudre certaines équations différentielles qui apparaissent dans la modélisation stochastique, par exemple.

Analyse complexe et applications des nombres complexes en finance et en trading

Les nombres complexes sont utilisés en finance pour plusieurs applications avancées, principalement en raison de leurs propriétés mathématiques uniques et des techniques analytiques qu'ils permettent.

Voici quelques raisons et contextes clés dans lesquels les nombres imaginaires sont utilisés en finance :

Modèles d'évaluation des options

Dans le cadre de Black-Scholes et d'autres modèles d'évaluation des options, l'utilisation de nombres complexes (principalement sous la forme de logarithmes et d'exponentielles complexes) facilite l'analyse de l'évaluation des options.

Par exemple, la transformée de Fourier (qui implique des nombres complexes) est utilisée dans certaines techniques avancées d'évaluation des options pour traiter les modèles dans lesquels la dynamique des prix de l'actif sous-jacent présente des sauts ou d'autres caractéristiques non standard.

Les modèles d'évaluation impliquent souvent la résolution d'équations différentielles pour lesquelles les techniques des nombres complexes sont utiles.

Gestion des risques et processus stochastiques

En mathématiques financières, les processus stochastiques (comme le mouvement brownien, qui sous-tend de nombreux modèles financiers) font souvent appel à l'analyse complexe pour trouver des solutions (en particulier lorsqu'il s'agit d'intégrales de chemin ou du calcul d'Ito).

Dans certaines techniques de gestion des risques, les nombres complexes sont utilisés pour modéliser le comportement des instruments financiers dans des conditions extrêmes ou pour simuler divers scénarios dans le cadre de tests de résistance.

Traitement des signaux dans le trading algorithmique

Les techniques de l'analyse complexe sont utilisées dans le traitement des signaux, qui est utilisé dans le trading algorithmique.

Par exemple, la transformation rapide de Fourier (FFT), une forme d'analyse dans le traitement des signaux, est fondée sur l'analyse complexe.

La FFT est utilisée pour analyser les composantes de fréquence des données de séries temporelles financières.

Cette analyse permet d'identifier les tendances, les cycles et les modèles périodiques dans les prix des actifs.

Analyse des séries temporelles (analyse des modèles cycliques ou saisonniers)

Les nombres complexes sont utilisés en économétrie et dans l'analyse des séries temporelles pour comprendre les modèles cycliques et saisonniers dans les données économiques.

La décomposition des séries temporelles en composantes tendancielles et saisonnières fait souvent appel à des techniques telles que la transformation discrète de Fourier (DFT) qui utilise des nombres complexes.

Analyse quantitative des taux d'intérêt

Dans certains modèles de taux d'intérêt, en particulier ceux qui impliquent des conditions de non-arbitrage dans un cadre financier à temps continu, l'analyse complexe peut fournir des solutions à des problèmes autrement insolubles.

Analogues en génie électrique

Dans des domaines tels que l'ingénierie électrique, les nombres complexes sont couramment utilisés pour analyser les circuits.

Ces techniques ont des analogues en ingénierie financière pour la modélisation des flux de trésorerie et des rendements, en particulier dans la structuration des produits dérivés et la gestion des risques.

Optimisation des portefeuilles et allocation d'actifs

Les nombres complexes peuvent également être utilisés dans certains modèles avancés d'optimisation de portefeuille.

Ces modèles nécessitent souvent la résolution de problèmes d'optimisation complexes où les mathématiques impliquées peuvent s'étendre aux nombres complexes (un nombre négatif est utilisé dans la solution d'une variable à la puissance d'un nombre pair).

L'analyse complexe dans la théorie économique

Cartographie conforme

Utilisée dans certains modèles économiques pour simplifier des systèmes économiques complexes ou des régions à des fins d'analyse.

Systèmes dynamiques

La dynamique complexe, un domaine qui utilise les méthodes de l'analyse complexe, peut être appliquée à l'étude du comportement chaotique dans les modèles économiques.

L'analyse complexe dans la théorie économique

Cartographie conforme

Utilisée dans certains modèles économiques pour simplifier des systèmes économiques complexes ou des régions à des fins d'analyse.

Systèmes dynamiques

La dynamique complexe, un domaine qui utilise les méthodes de l'analyse complexe, peut être appliquée à l'étude du comportement chaotique dans les modèles économiques.

La géométrie complexe en finance

Comme nous l'avons vu dans d'autres articles, les données financières peuvent souvent être étudiées d'un point de vue géométrique et topologique.

La géométrie complexe intervient, en utilisant des outils tels que les équations différentielles et les manifolds, pour naviguer dans ces courbes.

Fixer le prix des options exotiques

Pour les instruments financiers complexes tels que les options arc-en-ciel ou les options à barrière, les modèles géométriques fournissent des mécanismes de tarification sophistiqués.

Modélisation des sourires de volatilité

Lorsque la volatilité implicite n'est pas constante, l'utilisation de méthodes géométriques permet de mieux refléter les réalités du marché.

Optimisation des portefeuilles

À l'instar de la recherche de l'itinéraire le plus efficace dans un espace déformé, la géométrie complexe peut aider à orienter l'allocation stratégique des actifs.

Bien qu'il s'agisse d'un domaine spécialisé, la géométrie complexe en finance ouvre de nouvelles perspectives.

En rapport:

• Géométrie différentielle

• Géométrie symplectique

• Manifolds riemanniens

• Apprentissage des manifolds

• Topologie différentielle

• Mécanique géométrique

Les nombres complexes dans les applications d'apprentissage automatique en finance

Dans les applications d'apprentissage automatique en finance, les nombres complexes permettent d'améliorer les algorithmes, notamment dans les tâches de représentation des données et de traitement des signaux.

Ils sont utilisés dans les réseaux neuronaux pour traiter et analyser les données de séries temporelles (par exemple, les cours de la bourse), où leur capacité à encoder des informations à la fois en termes de magnitude et de phase est précieuse.

Cette capacité est utile pour des tâches telles que la détection des anomalies, l'analyse des tendances et la modélisation prédictive.

Les réseaux neuronaux à valeurs complexes (qui exploitent les nombres complexes) peuvent offrir de meilleures performances dans certaines applications financières en traitant efficacement les données présentant des relations de périodicité et de phase inhérentes (une caractéristique commune aux marchés financiers).

Leur efficacité dépend toutefois du problème spécifique, des caractéristiques des données et de la complexité des calculs.

Exemple de codage - Analyse complexe et nombres complexes en finance

Prenons un exemple dans lequel nous utilisons Python pour calculer la transformée de Fourier d'une simple série chronologique financière.

La transformation de Fourier, utile dans le traitement des signaux, peut être appliquée aux données financières pour identifier les composantes périodiques ou les tendances.

Cet exemple démontrera l'utilisation des nombres complexes dans un tel contexte.

Supposons que nous disposions d'une série temporelle simple représentant les prix de clôture d'une action sur un certain nombre de jours.

Nous utiliserons la transformation de Fourier rapide (FFT), une version efficace de la transformation de Fourier discrète, pour analyser cette série temporelle.

Tout d'abord, Python doit être installé avec la bibliothèque NumPy, qui prend en charge les tableaux et matrices multidimensionnels de grande taille, ainsi qu'une collection de fonctions mathématiques permettant d'opérer sur ces tableaux.

• Nous commencerons par créer une simple liste stock_prices pour représenter les cours des actions sur une période donnée (pour simplifier, 10 jours).

• Nous utiliserons la fonction np.fft.fft pour calculer la transformée de Fourier rapide de cette série temporelle. Cette opération implique des nombres complexes, puisque le résultat fft_result est un tableau de nombres complexes.

• Les fréquences correspondant à ces composantes sont calculées à l'aide de la fonction np.fft.fftfreq.

• Nous traçons ensuite la série temporelle originale et les amplitudes des résultats de la FFT. Le tracé de l'amplitude donne une idée des fréquences significatives dans les données.

import numpy as np
import matplotlib.pyplot as plt

# Example stock prices over 10 days
stock_prices = [100, 101, 102, 103, 102, 101, 100, 99, 98, 99]

# Compute the Fast Fourier Transform (FFT)
fft_result = np.fft.fft(stock_prices)

# Compute frequencies associated with FFT components
freq = np.fft.fftfreq(len(stock_prices))

# Plotting the original time series
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(stock_prices, color='blue')
plt.title('Original Stock Price Time Series')
plt.xlabel('Time (days)')
plt.ylabel('Price')

# Plotting the magnitudes of the FFT results
plt.subplot(1, 2, 2)
plt.stem(freq, np.abs(fft_result), 'b', markerfmt=" ", basefmt="-b")
plt.title('Magnitude of FFT Coefficients')
plt.xlabel('Frequency')
plt.ylabel('Magnitude')

plt.tight_layout()
plt.show()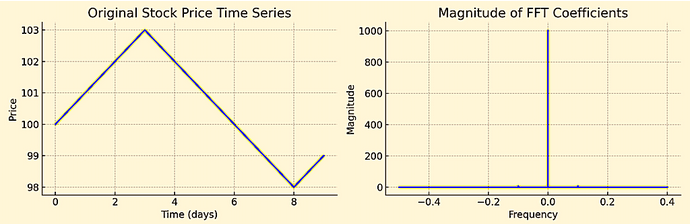

Défis et limites

Complexité

Les méthodes d'analyse complexe peuvent être mathématiquement intensives et ne sont pas toujours intuitives pour les praticiens de la finance qui n'ont pas de solides connaissances en mathématiques.

Naturellement, elles se limitent principalement à des formes spécialisées d'ingénierie financière, de trading quantique ou de recherche théorique.

Risque lié au modèle

En finance, les modèles faisant appel à des analyses complexes doivent être utilisés avec prudence.

Cela dépend du problème à résoudre et de la connaissance de la (des) technique(s) applicable(s) à utiliser.

Conclusion

L'analyse complexe a des applications en finance, sur les marchés et dans le trading - dans des domaines tels que la tarification des produits dérivés, la gestion des risques et le trading algorithmique.

Néanmoins, l'applicabilité et l'efficacité de ces méthodes dépendent fortement des hypothèses des modèles sous-jacents et des compétences des praticiens dans l'application de ces outils mathématiques à des scénarios réels.

Brokers d'options

Investir comporte des risques de perte

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.