#1 30-01-2024 15:19:13

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 231

Manifolds riemanniens dans la finance, les marchés et le trading

Les manifolds de Riemann sont des constructions mathématiques issues de la géométrie différentielle, qui ont des applications dans diverses disciplines, y compris la finance et le trading quantique.

Nous couvrirons à la fois les concepts fondamentaux des manifolds de Riemann et leurs applications pratiques dans des contextes financiers.

Principaux enseignements

Cadre géométrique

• Les manifolds riemanniens fournissent un cadre géométrique pour modéliser les structures et les dynamiques non linéaires des marchés.

• Ils permettent aux traders d'analyser et de visualiser les marchés financiers dans un espace multidimensionnel.

Analyse du risque et de la corrélation

• En représentant les actifs financiers ou les portefeuilles comme des points sur un manifold, les traders peuvent analyser plus efficacement les risques et les corrélations.

• Cela peut conduire à une meilleure diversification des portefeuilles et à des stratégies de gestion des risques.

Perspectives prédictives

• L'utilisation de la courbure et de la topologie des manifolds permet d'identifier les tendances et les anomalies.

Exemple de codage

• Nous fournissons un exemple de codage des manifolds riemanniens plus loin dans l'article.

Concepts de la géométrie riemannienne et des manifolds riemanniens

Un manifold riemannien est un cadre dans lequel chaque point est associé à un espace*, ce qui permet de mesurer les distances et les angles de manière fluide et continue.

Ce produit intérieur varie doucement d'un point à l'autre.

(*Un espace, dans un contexte mathématique, est un ensemble d'éléments ainsi qu'un ensemble de règles ou de propriétés définissant la manière dont ces éléments sont liés les uns aux autres).

Tenseur métrique

L'élément clé d'un manifold riemannien est le tenseur métrique, qui définit la manière dont les distances et les angles sont mesurés.

Géodésiques

Il s'agit des "chemins les plus courts" entre les points d'un manifold, semblables aux lignes droites de la géométrie euclidienne.

En finance, elles peuvent représenter des chemins ou des stratégies optimales.

Courbure

Il s'agit de la façon dont un manifold s'écarte de la planéité.

La courbure peut avoir diverses interprétations dans les modèles financiers, en fonction de ce qui est modélisé.

Les formes de modélisation les plus courantes concernent le risque (par exemple, la volatilité), les prix et d'autres variables qui peuvent être non linéaires.

Applications dans le domaine de la finance, des marchés et du trading

Optimisation des portefeuilles

Les manifolds riemanniens peuvent être utilisés pour modéliser l'espace des portefeuilles de négociation/d'investissement.

Les géodésiques de ce manifold peuvent représenter des chemins efficaces pour le rééquilibrage des portefeuilles ou la transition entre les portefeuilles (c'est-à-dire le passage d'une allocation d'actifs à une autre).

Vous trouverez ci-dessous un exemple de manifold statistique 3D dans lequel vous essayez d'optimiser un portefeuille composé de cinq actifs différents présentant le même risque et le même rendement et dont les corrélations sont nulles.

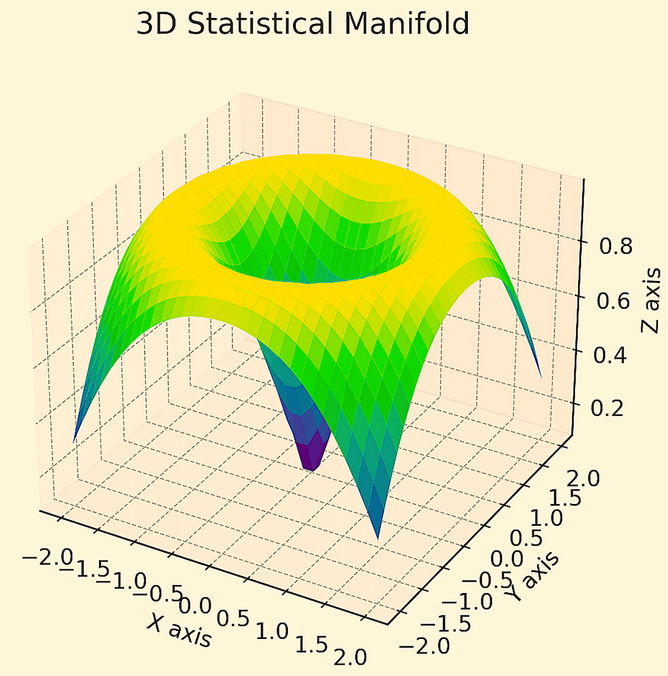
Des niveaux élevés de courbure indiquent généralement des répartitions de portefeuille très sensibles aux changements des conditions économiques actualisées (et représentent donc des formes sous-optimales d'optimisation de portefeuille par rapport à d'autres solutions).

Les portefeuilles situés dans des parties plus plates du collecteur indiquent des portefeuilles plus équilibrés et moins sensibles à ces changements.

Les types de portefeuilles les plus susceptibles d'être traités favorablement par les interprétations géométriques différentielles sont ceux qui sont bien diversifiés, de sorte qu'ils obtiennent de bons résultats dans toute une série de contextes de croissance, d'inflation, de taux d'intérêt et d'autres environnements qui entraînent des changements dans les portefeuilles.

Quelques articles ci-dessous expliquent comment procéder :

• Bêta équilibré

• Comment construire un portefeuille équilibré

• Portefeuilles à 3 et 4 actifs

• Portefeuille tous temps

Gestion du risque

La courbure du manifold peut être liée au risque sur les marchés financiers.

Les zones de forte courbure peuvent représenter une plus grande volatilité ou instabilité du marché.

Modèles d'évaluation des options

Dans certains modèles avancés, l'espace des prix possibles de l'actif sous-jacent dans le temps peut être représenté sous la forme d'un manifold riemannien.

Cela peut permettre une compréhension plus nuancée ou plus précise de l'évaluation des options.

Dynamique des marchés

Les manifolds peuvent modéliser la structure complexe des marchés financiers, là où la géométrie euclidienne traditionnelle ne suffit pas.

Cela peut permettre de mieux comprendre le comportement des marchés et les mouvements des prix des actifs.

De nombreux modèles financiers supposent des linéarités dans l'établissement des prix ou sont trop simplifiés.

Trading algorithmique

Dans le domaine du trading algorithmique, les manifolds riemanniens peuvent être utilisés pour optimiser les trajectoires d'exécution des transactions dans des environnements de marché complexes et de haute dimension.

Modèles de taux d'intérêt

La modélisation de la structure à terme des taux d'intérêt peut également être abordée à l'aide de la géométrie riemannienne, afin de saisir les complexités des mouvements de la courbe de rendement.

Manifolds riemanniens et apprentissage automatique

Les manifolds riemanniens dans l'apprentissage automatique permettent de modéliser des structures de données complexes et non linéaires dans un espace géométrique.

Cette approche facilite la compréhension et l'analyse des données à haute dimension en fournissant un cadre pour capturer les propriétés géométriques intrinsèques.

Elle améliore les algorithmes pour des tâches telles que le regroupement et la réduction de la dimensionnalité. Elle améliore leurs performances sur les ensembles de données dont les structures sous-jacentes ne sont pas euclidiennes.

En tirant parti de la courbure et de la topologie de ces manifolds, les modèles d'apprentissage automatique peuvent représenter plus précisément les données du monde réel.

Cela peut conduire à une amélioration de la précision de l'apprentissage et du pouvoir prédictif dans des applications allant de la vision par ordinateur au traitement du langage naturel, en passant par les différents types de cadres mathématiques, statistiques et probabilistes utilisés dans la finance et le trading quantique.

Les mathématiques derrière les manifolds de Riemann

Voici quelques équations mathématiques de base en rapport avec les manifolds de Riemann et leurs applications potentielles dans le domaine de la finance :

Tenseur métrique

Le tenseur métrique, g_{ij}, définit le produit intérieur sur l'espace tangent en chaque point du collecteur.

Cela signifie qu'en chaque point du manifold, g_{ij} fournit un produit intérieur qui permet de mesurer les distances et les angles dans l'espace tangent en ce point.

Il définit donc une notion locale de géométrie sur le manifold.

En finance, il pourrait s'agir de définir une métrique du risque sur un espace de portefeuille (c'est-à-dire une certaine allocation d'actifs).

Tenseur de courbure de Riemann

Le tenseur de courbure de Riemann, R_{ijkl}, décrit comment la métrique varie d'un point à l'autre du manifold.

Il mesure la non-platitude.

Dans le contexte financier, la courbure peut représenter la manière dont le risque varie d'un portefeuille à l'autre.

Courbure de Ricci

La courbure de Ricci, Ric_{ij}, est une trace du tenseur de Riemann et mesure le degré auquel le volume d'une boule géodésique s'écarte de celui d'une boule dans l'espace euclidien.

En finance, la courbure de Ricci pourrait indiquer à quel point le risque d'un portefeuille se concentre à mesure que l'on se déplace dans l'espace du portefeuille.

Courbure scalaire

La courbure scalaire, R, est la trace du tenseur de Ricci et donne une mesure de la courbure totale en un point.

Dans le cadre du trading quantique, une courbure scalaire plus élevée peut indiquer une plus grande concentration du risque global pour un portefeuille donné.

Opérateur de Laplace-Beltrami

L'opérateur de Laplace-Beltrami, Δ, agit sur les fonctions du manifold.

En finance, l'opérateur LB pourrait représenter un opérateur différentiel de sensibilité au risque qui fixe le prix des actifs en fonction des variations du risque.

Résumé

En résumé, les concepts géométriques clés tels que la métrique, la connexion, la courbure et les opérateurs différentiels sur un manifold pourraient être utilisés pour mesurer le risque financier dans un espace de portefeuille de différentes manières.

Les équations relient le risque en différents points et avec différentes directions dans l'espace du portefeuille.

Défis et considérations

Complexité

L'application des manifolds riemanniens à la finance est mathématiquement complexe et nécessite une compréhension approfondie de la géométrie différentielle et de la théorie financière.

Données et calcul

La mise en œuvre de ces modèles nécessite une solide infrastructure de données et d'importantes ressources informatiques.

Interprétation

La nature abstraite de ces modèles nécessite une interprétation minutieuse afin d'appliquer les conclusions de manière significative dans des contextes financiers réels.

Bien que les manifolds riemanniens ne soient pas courants dans la pratique financière quotidienne, ils offrent un cadre pour la modélisation et la compréhension de phénomènes financiers complexes qui dépassent les capacités des modèles linéaires traditionnels.

Leur utilisation est plus importante dans la finance quantitative théorique et avancée, en particulier dans les domaines nécessitant une modélisation mathématique sophistiquée.

Exemple de codage

L'application directe des manifolds riemanniens à un problème financier spécifique en Python nécessite une compréhension de la géométrie différentielle et du contexte financier spécifique.

Nous pouvons illustrer un exemple de base qui montre comment un concept de manifold riemannien peut être intégré dans un scénario d'analyse financière, tel que l'optimisation de portefeuille.

Considérons un scénario simplifié dans lequel nous voulons modéliser l'espace des portefeuilles de trading/investissement comme un collecteur et calculer la géodésique (le chemin le plus court) entre deux portefeuilles.

Nous tracerons un graphique simplifié en 3D représentant un manifold sphérique avec deux points marqués sur celui-ci, symbolisant deux portefeuilles différents.

La sphère sert d'espace financier conceptuel et les points (portefeuilles) sont positionnés sur sa surface.

Dans un contexte financier plus avancé et plus spécifique, le chemin reliant ces points pourrait représenter une stratégie de transition optimale entre les deux portefeuilles.

import matplotlib.pyplot as plt

import numpy as np

from mpl_toolkits.mplot3d import Axes3D


# Function to create a sphere (representing the manifold)

def create_sphere(radius=1, step=0.1):

u = np.arange(0, 2 * np.pi, step)

v = np.arange(0, np.pi, step)

x = radius * np.outer(np.cos(u), np.sin(v))

y = radius * np.outer(np.sin(u), np.sin(v))

z = radius * np.outer(np.ones(np.size(u)), np.cos(v))

return x, y, z


# Define two portfolios (points on the sphere)

portfolio_1 = np.array([1, 0, 0]) # Point on the surface of the sphere

portfolio_2 = np.array([-1, 0, 0]) # Another point on the surface of the sphere


# Create the sphere

x, y, z = create_sphere()


# Plot the sphere and the portfolios

fig = plt.figure(figsize=(8, 8))

ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(x, y, z, color='b', alpha=0.3)

# Mark the portfolios

ax.scatter(portfolio_1[0], portfolio_1[1], portfolio_1[2], color='red', s=50, label='Portfolio 1')

ax.scatter(portfolio_2[0], portfolio_2[1], portfolio_2[2], color='green', s=50, label='Portfolio 2')

ax.legend()

plt.show()

Manifolds riemanniens et autres types de manifolds et applications en finance

Les manifolds de Riemann et les autres types de manifolds ont chacun des applications potentielles en finance.

Il est important de comprendre les différences entre ces manifolds pour apprécier leur applicabilité dans divers contextes financiers.

Les manifolds riemanniens

Les manifolds riemanniens sont des manifolds lisses dotés d'une métrique riemannienne, qui permet de définir la longueur, les angles et le volume.

Cette métrique est un produit intérieur positif-défini sur l'espace tangent en chaque point.

Voici quelques exemples d'applications dans le domaine de la finance :

Optimisation de portefeuille

Le tenseur métrique peut représenter la structure de risque de différents actifs, où les géodésiques représentent les transitions optimales entre les portefeuilles.

Mesure du risque

La courbure d'un manifold riemannien peut être interprétée comme un risque financier, les zones de forte courbure indiquant un risque plus élevé.

Manifolds symplectiques

Définis dans le contexte de la mécanique hamiltonienne, les manifolds symplectiques sont de dimension paire et dotés d'une forme symplectique, une 2-forme différentielle fermée non dégénérée.

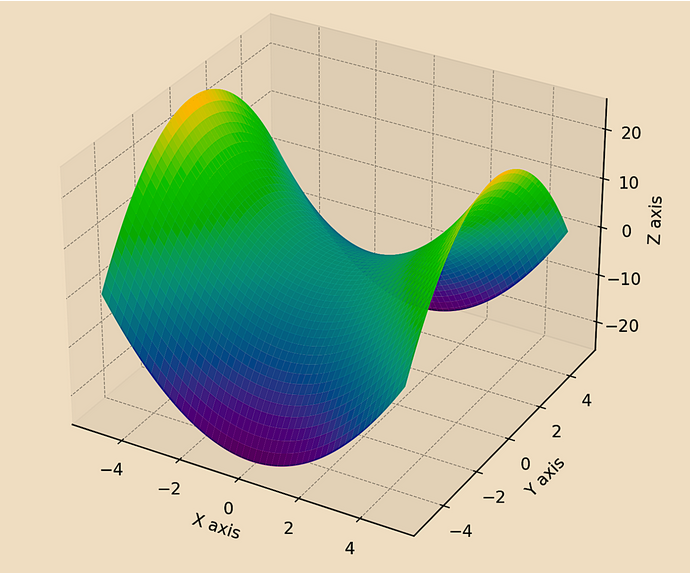
Application

Utilisée en finance quantitative pour modéliser la dynamique des systèmes de marché, où la structure symplectique peut représenter des lois de conservation (comme la conservation du capital) ou modéliser les paramètres d'un type de problème spécifique.

Manifolds complexes

Il s'agit de manifolds avec une structure complexe.

Ils permettent de passer des coordonnées réelles aux coordonnées complexes.

Application

Dans des domaines tels que l'évaluation des produits dérivés, où l'analyse complexe peut fournir des solutions plus nuancées.

Groupes de Lie

Manifolds lisses qui sont également des groupes et dont les opérations de groupe sont lisses.

Application

Modélisation de l'évolution des prix et des rendements sur les marchés financiers. Ils peuvent représenter les symétries continues et la dynamique des instruments financiers.

Manifolds de Finsler

Généralisations des manifolds riemanniens, où la métrique est définie sur le faisceau tangent et n'est pas nécessairement quadratique.

Application

Potentiellement utiles dans la gestion des risques et l'optimisation des portefeuilles, et un cadre plus général que les manifolds de Riemann.

Manifold hermitien

Un manifold hermitien est un espace dans lequel des points de données complexes sont reliés par une mesure cohérente d'angles et de longueurs à valeur complexe.

Application

Peut être utilisé pour modéliser des instruments financiers complexes ou des scénarios où l'amplitude et la phase (comme le prix et l'élan dans les transactions) sont essentielles pour améliorer l'analyse des produits dérivés complexes ou l'évaluation des risques.

Manifold sous-riemannien

Il s'agit d'un manifold dont la métrique n'est définie que sur un sous-ensemble de toutes les directions tangentes possibles.

Application

Il est utilisé dans des situations où seules des informations partielles sont disponibles ou dans des ensembles de données à haute dimension avec des contraintes.

Manifold pseudo-riemannien

Un manifold pseudo-riemannien généralise les manifolds riemanniens en permettant à la métrique d'avoir une signature indéfinie.

Application

Cette méthode permet de modéliser des scénarios avec des profils de risque et de rendement non standard.

Utile pour la modélisation avancée des risques et pour comprendre les marchés présentant des propriétés de volatilité et de stabilité atypiques.

Comparaison et applications financières

Flexibilité

Les manifolds riemanniens (avec leurs propriétés métriques bien définies) conviennent aux applications où les notions de distance et d'angle sont importantes, comme dans l'évaluation des risques et l'optimisation des portefeuilles.

Les manifolds de Finsler offrent plus de flexibilité, mais au prix d'une complexité accrue.

Principes de conservation

Les manifolds symplectiques sont particulièrement pertinents dans les domaines de la finance qui peuvent être modélisés par des lois de conservation, semblables à celles de la physique, comme dans certains modèles dynamiques de marché.

Analyse complexe

Les manifolds complexes sont utiles dans les domaines où l'analyse complexe fournit de meilleures solutions, comme certains types de modèles d'évaluation des produits dérivés.

Dynamique des marchés financiers

Les groupes de Lie sont utiles pour comprendre la dynamique continue des instruments financiers, comme la modélisation du flux des prix et des rendements dans le temps.

Conclusion

Si les manifolds de Riemann sont utiles en finance pour modéliser des scénarios dans lesquels des concepts géométriques tels que la distance et la courbure sont applicables, d'autres types de manifolds offrent également des perspectives uniques adaptées à différentes applications financières.

Le choix du manifold dépend des caractéristiques spécifiques du problème financier et des hypothèses sous-jacentes sur le comportement du marché et la dynamique des instruments.

Brokers d'options

Investir comporte des risques de perte

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.