#1 28-01-2024 21:18:12

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 231

La géométrie symplectique dans la finance, les marchés et le trading (exemple de codage)

La géométrie symplectique, issue de la mécanique classique, est une branche de la géométrie différentielle qui s'intéresse aux manifestes symplectiques (une manière de représenter et de visualiser des données non linéaires).

Un manifold symplectique est un collecteur lisse équipé d'une forme 2 fermée, non dégénérée, connue sous le nom de forme symplectique.

Ce domaine a trouvé des applications dans divers secteurs, dont la finance, en particulier dans le contexte du trading quantitatif et algorithmique.

Principaux enseignements

Amélioration de la modélisation des marchés

• La géométrie symplectique offre des méthodes avancées pour modéliser des dynamiques de marché uniques.

• Elle permet de mieux comprendre le comportement des marchés.

Gestion des risques

• L'utilisation de structures symplectiques peut améliorer la compréhension et la gestion des risques des portefeuilles, en particulier dans les stratégies de trading plus complexes et axées sur les quant.

Efficacité du trading algorithmique

• Les intégrateurs symplectiques aident à développer des algorithmes plus précis et plus stables pour le trading quantitatif et algorithmique, et à modéliser leur évolution dans le temps.

Applications en finance

Trading quantitatif et algorithmique

La géométrie symplectique peut trouver des applications dans la modélisation et l'analyse de la dynamique des marchés.

Les algorithmes peuvent utiliser des intégrateurs symplectiques, qui sont des méthodes numériques préservant la structure symplectique, et modéliser l'évolution temporelle des marchés.

Gestion des risques et optimisation des portefeuilles

Les concepts de la dynamique hamiltonienne peuvent être utilisés pour aider à modéliser l'évolution des portefeuilles et des marchés financiers.

Tarification des produits dérivés

Certains modèles de tarification des produits dérivés pourraient bénéficier des connaissances géométriques fournies par la géométrie symplectique dans certains cas.

Analyse de la microstructure du marché et liquidité

L'étude des mécanismes détaillés du déroulement des transactions et de leur incidence sur l'évaluation des actifs peut être améliorée par des méthodes symplectiques.

Ces outils peuvent être utilisés pour comprendre le flux et l'impact des ordres sur un marché, ainsi que la dynamique de la liquidité.

Jeux ou paris à gains discrets

Dans une situation où :

• les jeux ou les paris sont assortis de gains discrets et

• les considérations sur le nombre de paris que vous prenez sont importantes...

...les manifolds symplectiques peuvent montrer le rendement/risque optimal.

Par exemple, plus loin dans l'article, nous utilisons l'exemple de la stratégie de sélection des tirs au basket-ball et de la manière dont elle pourrait être modélisée. Tirer très près du panier peut être très efficace parce que ces tirs sont les plus faciles à réaliser, mais tirer plus de tirs à 3 points vous donne 50 % de valeur en plus par tir réalisé.

On peut donc se trouver dans une situation où la distribution est bimodale (tirs courts et tirs longs), où l'on veut tirer efficacement (ni trop de tirs, ni trop peu) et où l'on obtient le meilleur rapport rendement/risque.

Cela peut donner un collecteur unique avec plus d'un point optimal.

En finance, cela peut s'apparenter à une approche d'investissement/de trading de type "barbell".

• Le manifold illustrerait l'interaction entre différents types d'investissements ou de transactions (à haut risque ou à faible risque) et leur impact sur la performance globale du portefeuille (ratio rendement/risque).

• Tout comme dans l'analogie du basket-ball, où il existe plusieurs points optimaux (tirs courts efficaces et tirs longs de grande valeur), dans le manifold symplectique financier, il peut y avoir plusieurs pics ou vallées représentant différentes combinaisons optimales de stratégies de trading/d'investissement.

• Ce manifold permettrait de visualiser comment la modification d'un aspect du portefeuille (comme l'ajout d'actifs à haut risque) affecte le profil risque/rendement global, aidant ainsi les traders/investisseurs à trouver le point d'équilibre qui correspond à leurs objectifs et à leur tolérance au risque.

Limites et défis

Complexité et abstraction

La géométrie symplectique est un domaine mathématiquement sophistiqué et abstrait, ce qui peut rendre difficile son application directe à la finance.

Limites de la modélisation

Les marchés financiers sont influencés par un large éventail de facteurs, y compris le comportement humain et les changements réglementaires, qui peuvent ne pas être facilement pris en compte par les méthodes géométriques.

Structure géométrique symplectique

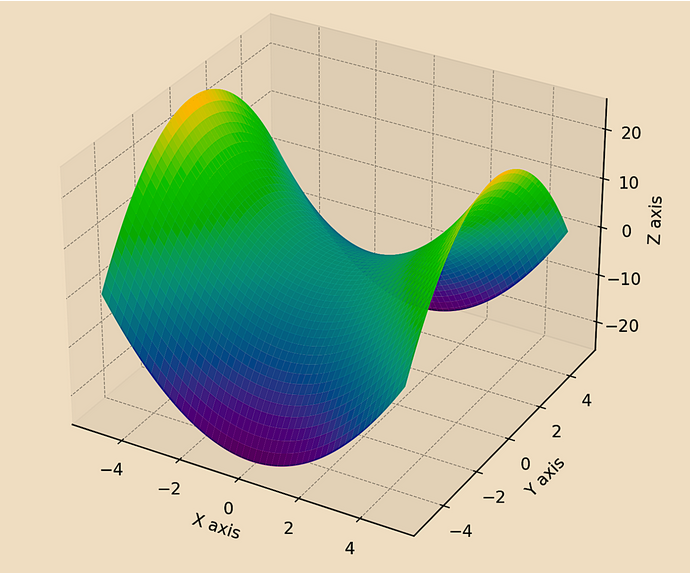
La visualisation ci-dessous représente un manifold symplectique simple.

Dans cet exemple, une surface en forme de selle est tracée en trois dimensions.

Ce type de surface est une représentation de base et peut être considéré comme un modèle simple de structure symplectique.

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Symplectic manifold visualization

# Define a grid
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)

# Define a symplectic form, e.g., a simple saddle as an example
z = x**2 - y**2

# Plotting
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis')

# Labels and title
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')
ax.set_title('Symplectic Manifold Representation')

plt.show()

Le manifold symplectique visualisé ici, bien qu'il s'agisse d'une représentation simplifiée, peut être considéré comme un outil permettant d'illustrer certains concepts financiers lorsque nous établissons des parallèles entre les dimensions du manifold et les variables financières.

Examinons quelques exemples hypothétiques :

1. Liquidité et exécution des transactions

• Axe X - Il pourrait représenter la taille d'une transaction ou d'un ordre (par exemple, une valeur négative signifie une position courte, une valeur positive une position longue).

• Axe Y - Il peut symboliser la liquidité de l'actif négocié.

• Axe Z - La surface peut alors illustrer l'impact de la taille de la transaction et de la liquidité de l'actif sur le prix d'exécution ou le dérapage. Des transactions plus importantes sur des actifs moins liquides peuvent entraîner un dérapage plus important, visualisé par la courbure du collecteur.

2. Jeu à gains discrets

• Axe des X (combinaison relative des paris) - Cet axe pourrait représenter le volume relatif des gains entre deux gains possibles. Pensez-y de manière analogue au pourcentage de tirs à 2 points par rapport au nombre de tirs à 3 points d'un joueur de basket-ball, l'axe des X représentant la distance par rapport au panier. Vous obtenez ce type de polarité courbe parce que les dunks et les layups sont les plus efficaces, que les tirs à 3 points vous apportent 50 % de valeur supplémentaire par tir et que les tirs à mi-distance vous apportent la même valeur qu'un dunk ou un layup, mais sont plus difficiles à réaliser.

• Axe Y (Momentum) - Volume des paris. Si vous effectuez trop peu de transactions ou si vous en faites trop, vos résultats ne seront pas optimaux. Comme au basket-ball, si vous ne tirez jamais, vous ne pouvez pas marquer ; si vous tirez trop, vous ne serez pas efficace. La polarité de la sélection des tirs (facilité des tirs par rapport à leur valeur) et l'équilibre dans la manière dont ils sont effectués conduisent à la forme de la selle.

• Axe Z (interaction) - La surface résultante pourrait alors illustrer le compromis risque-rendement. En prenant les paris appropriés dans le bon volume, on obtient le meilleur rapport rendement-risque. De même, au basket-ball, prendre des dunks et des layups lorsqu'ils sont disponibles, associés à des tirs à 3 points efficaces (plus de valeur), est un mélange qui pourrait bien fonctionner.

Conclusion

Bien que la géométrie symplectique ne soit pas le courant dominant de l'analyse financière, ses applications offrent des perspectives intéressantes, principalement dans les domaines où la dynamique des systèmes financiers est importante.

Néanmoins, l'efficacité de ces applications dépend fortement du contexte spécifique et de la capacité à traduire des concepts mathématiques abstraits en stratégies financières pratiques.

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.