Programmation quadratique dans le trading et l'investissement

Climax · 06-02-2024 16:13:11

La programmation quadratique dans le trading et l'investissement (exemple de codage)

La programmation quadratique (PQ) est un type d'optimisation mathématique utilisé dans la gestion de portefeuille et les stratégies de trading/investissement.

Sa fonction première est d'optimiser l'allocation des actifs afin d'obtenir les meilleurs rendements possibles ajustés au risque.

Principaux enseignements :

Optimise l'allocation du portefeuille - La programmation quadratique permet de déterminer la répartition optimale des actifs afin de maximiser les rendements pour un niveau de risque donné.
Gère efficacement le risque - Elle aide à minimiser le risque du portefeuille en calculant la matrice de variance-covariance des rendements des actifs, ce qui permet de mettre en place des stratégies de gestion du risque plus précises.
Amélioration de la diversification - La programmation quadratique permet d'identifier des stratégies d'allocation d'actifs non évidentes qui améliorent la diversification du portefeuille et réduisent la volatilité.
Exemple de codage - Un exemple de codage de la programmation quadratique est présenté plus loin dans l'article.

Comprendre la programmation quadratique

La programmation quadratique consiste à minimiser ou à maximiser une fonction quadratique soumise à des contraintes linéaires.

Dans le contexte de la négociation et de l'investissement, la fonction quadratique représente généralement la variance (ou le risque) du portefeuille :

la fonction quadratique représente généralement la variance (ou le risque) du portefeuille, et
les contraintes linéaires peuvent refléter des limitations budgétaires, des plafonds d'exposition au risque ou d'autres lignes directrices en matière d'investissement.

Les mathématiques de la programmation quadratique

Voici un aperçu de la programmation quadratique pour l'optimisation de portefeuille :

Le problème d'optimisation consiste à maximiser le rendement du portefeuille tout en minimisant le risque :

Maximiser : Rp = wTμ
Minimiser : Vp = wT Σ w
Sous réserve de : Σ wi = 1 (entièrement investi) L ≤ wi ≤ U (limites de poids des actifs).

Où :

w = Vecteur des pondérations des actifs dans le portefeuille
μ = Vecteur des rendements attendus des actifs
Σ = matrice de covariance des rendements des actifs
Rp = Rendement du portefeuille
Vp = Variance (risque) du portefeuille
L, U = Limites inférieure et supérieure des actifs

Il s'agit d'un problème de programmation quadratique avec une fonction objective quadratique (variance du portefeuille) et des contraintes linéaires (budget, limites).

Les pondérations optimales des actifs w* sont obtenues en résolvant :

Minimiser : (1/2)wT Σ w (sous réserve des contraintes linéaires)

La programmation quadratique utilise des méthodes numériques itératives telles que l'ensemble actif ou le point intérieur pour résoudre la question de la répartition optimale des actifs.

Le résultat est le portefeuille situé sur la "frontière efficiente", c'est-à-dire le rendement le plus élevé pour un niveau de risque donné et qui satisfait aux contraintes (voir ci-dessous).

La forme quadratique permet d'intégrer la covariance entre les actifs et l'impact de la diversification.

Applications dans l'optimisation de portefeuille

Minimisation du risque

La programmation quadratique est utilisée dans l'analyse moyenne-variance, un cadre introduit par Harry Markowitz en 1952.

Les traders utilisent la PQ pour construire un portefeuille qui offre le rendement attendu le plus élevé pour un niveau de risque donné.

Ou encore, le risque le plus faible pour un niveau donné de rendement attendu.

En résolvant un problème de QP, les traders peuvent identifier les pondérations des actifs qui minimiseront la variance globale du portefeuille.

Allocation d'actifs

Les traders utilisent également la programmation quadratique pour répartir les actifs en fonction de leur tolérance au risque et de leurs objectifs.

Il s'agit d'équilibrer le compromis entre le risque et le rendement, d'assurer la diversification et de respecter les contraintes de leur stratégie.

Avantages pour le trading et l'investissement

Identification de la frontière efficiente

La programmation quadratique permet aux traders de localiser la frontière efficiente, un ensemble de portefeuilles optimaux qui offrent le rendement attendu le plus élevé pour un niveau de risque donné.

Graphiquement, la frontière efficiente se présente comme suit, la partie bleu foncé du graphique (dans ce cas) étant considérée comme l'allocation optimale.

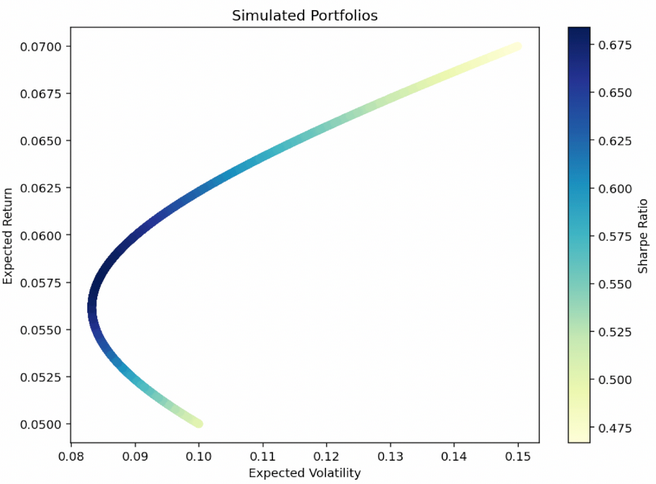
Cette identification est importante pour l'allocation stratégique des actifs et aide les traders à prendre des décisions en fonction de leur appétit pour le risque.

Personnalisation des stratégies de trading et d'investissement

QP permet de personnaliser les stratégies de trading/investissement en incorporant diverses contraintes, telles que des limitations sur les ventes à découvert, des plafonds spécifiques à un actif ou à un secteur, ou des exigences minimales d'investissement.

Cette flexibilité garantit que le portefeuille optimisé s'aligne sur les préférences individuelles et les exigences réglementaires.

Défis, critiques et considérations

Hypothèses du modèle

La programmation quadratique repose sur certaines hypothèses, notamment la distribution normale des rendements et la stabilité des covariances dans le temps.

Les traders doivent être conscients de ces hypothèses et prendre en compte leurs implications sur la précision prédictive du modèle.

Complexité informatique

La résolution de problèmes de programmation quadratique à grande échelle peut être très exigeante sur le plan informatique.

C'est particulièrement vrai lorsqu'il s'agit de vastes univers d'actifs ou de structures de contraintes complexes.

Il est important de disposer d'algorithmes efficaces et de ressources informatiques performantes pour relever ces défis.

Manque de dimensionnalité

Le cadre moyenne-variance ne prend souvent pas en compte le niveau élevé de dimensionnalité inhérent aux données financières et au processus d'optimisation.

C'est pourquoi la finance quantitative moderne s'oriente de plus en plus vers des approches géométriques plus sophistiquées qui prennent en compte la dimensionnalité, comme celles décrites dans les articles ci-dessous :

En rapport:

Méthode de la ligne critique

La méthode de la ligne critique est une approche algorithmique utilisée en optimisation de portefeuille (notamment pour résoudre le problème d'optimisation de la moyenne-variance formulé par Harry Markowitz).

Cette méthode identifie efficacement l'allocation optimale des actifs qui maximise le rendement pour un niveau de risque donné ou minimise le risque pour un niveau de rendement donné.

Elle fonctionne en construisant la frontière efficiente, un ensemble de portefeuilles optimaux, par le biais de la programmation linéaire et quadratique.

La méthode de la ligne critique se distingue par sa précision dans la gestion des contraintes complexes du monde réel, telles que les seuils d'achat, les limites des actifs et les coûts de transaction.

Son processus progressif et systématique navigue à travers ces contraintes, en ajustant les pondérations des actifs pour trouver les portefeuilles les plus efficaces.

Cette méthode reste fondamentale dans la théorie moderne du portefeuille, car elle permet de prendre des décisions d'allocation stratégique davantage fondées sur des données.

Programmation quadratique et ingénierie financière

La programmation quadratique fait partie de l'ingénierie financière.

En minimisant la fonction de coût quadratique - généralement la variance du portefeuille - la programmation quadratique permet aux traders de trouver l'allocation d'actifs optimale qui permet d'obtenir les rendements souhaités pour un niveau de risque donné.

Cette approche s'appuie sur la matrice de covariance des rendements des actifs pour répartir efficacement les allocations entre les actifs et équilibrer le compromis entre le risque et le rendement.

Grâce à la PQ, les ingénieurs financiers peuvent construire systématiquement des portefeuilles diversifiés qui correspondent à la tolérance au risque et aux objectifs des traders, et renforcer la rigueur scientifique dans la gestion de portefeuille.

Exemple de codage - Programmation quadratique

Pour optimiser l'allocation du portefeuille à l'aide de la programmation quadratique, nous devons définir notre problème d'optimisation.

L'objectif est généralement de maximiser le rendement attendu du portefeuille pour un niveau de risque donné (ou de minimiser le risque pour un niveau de rendement attendu donné), sous réserve que la somme des pourcentages d'allocation soit égale à 100 %.

Dans de nombreux autres articles, nous avons utilisé cette répartition des actifs et cet ensemble d'hypothèses pour nos exemples :

Actions : Rendement à terme de +6 %, volatilité annualisée de 15 % en utilisant l'écart-type
Obligations : Rendement à terme de +4 %, volatilité annualisée de 10 % en utilisant l'écart-type
Matières premières : Rendement à terme de +3%, volatilité annualisée de 15% en utilisant l'écart-type
Or : +3% de rendement à terme, 15% de volatilité annualisée en utilisant l'écart-type

Nous allons mettre en place une optimisation de base qui minimise le risque pour un rendement attendu donné.

Nous supposerons également qu'il n'y a pas de vente à découvert et que la somme des allocations est de 100 %.

Nous pouvons utiliser la bibliothèque Python cvpxy pour cette tâche.

Si vous ne l'avez pas installée, vous pouvez l'installer à l'aide de pip :

pip install cvxpy

Le code :

import cvxpy as cp
import numpy as np

# Forward returns & standard deviations (volatilities)
returns = np.array([0.06, 0.04, 0.03, 0.03])
volatilities = np.array([0.15, 0.10, 0.15, 0.15])

# Assuming no correlation among assets for simplicity. In practice, you'd include a covariance matrix.
# Here, let's do a diagonal covariance matrix from volatilities for simplicity.
covariance_matrix = np.diag(volatilities ** 2)

# Decision variables: allocations to each asset
allocations = cp.Variable(4)

# Objective: Minimize portfolio variance (risk)
objective = cp.Minimize(cp.quad_form(allocations, covariance_matrix))

# Constraints
constraints = [
cp.sum(allocations) == 1, # Means sum of allocations = 100%
allocations >= 0, # Means no short selling
# You can add a constraint for a minimum expected return if you want
# cp.matmul(returns, allocations) >= target_return,
]

# Problem
problem = cp.Problem(objective, constraints)

# Solve the problem
problem.solve()

# Results
print("Optimal allocations:")
print(f"Stocks: {allocations.value[0]*100:.2f}%")
print(f"Bonds: {allocations.value[1]*100:.2f}%")
print(f"Commodities: {allocations.value[2]*100:.2f}%")
print(f"Gold: {allocations.value[3]*100:.2f}%")
print(f"Portfolio Risk (Standard Deviation): {np.sqrt(problem.value):.4f}")

Ce code trouvera l'allocation optimale qui minimise la variance du portefeuille compte tenu de la contrainte selon laquelle la somme de toutes les allocations doit être égale à 100 % et chaque allocation doit être non négative.

L'optimisation réelle peut aboutir à une allocation conservatrice puisqu'elle minimise strictement le risque sans tenir compte d'un rendement cible spécifique (ou d'un risque cible).

L'ajustement de l'objectif ou l'ajout d'une contrainte de rendement minimum attendu modifierait l'allocation pour atteindre cet objectif de rendement attendu.

Conclusion

La programmation quadratique est fondamentale pour l'optimisation des portefeuilles.

Sa capacité à équilibrer le risque et le rendement, tout en respectant diverses contraintes, la rend précieuse pour les traders/investisseurs qui cherchent à maximiser la performance de leurs portefeuilles.

Néanmoins, l'efficacité de la PQ dépend de la précision des entrées du modèle et des ressources informatiques disponibles.

Cela souligne l'importance d'une modélisation robuste et des capacités technologiques dans les stratégies modernes de trading et d'investissement.

#1 06-02-2024 16:13:11