Calcul de la variance pour le trading et l'investissement
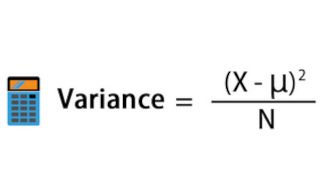
La variance joue un rôle important dans le trading et l'investissement car elle mesure le degré de dispersion des rendements autour du rendement moyen.
En d'autres termes, la variance indique dans quelle mesure les rendements d'un titre ou d'un portefeuille s'écartent de son rendement moyen.
Les investisseurs et les traders utilisent la variance (volatilité) pour estimer le risque d'un investissement.
Une variance plus élevée signifie que l'incertitude et le risque associés à l'investissement sont plus importants, tandis qu'une variance plus faible indique un risque moindre.
Principaux points à retenir - Variance
- La variance mesure le degré de dispersion des rendements autour du rendement moyen d'un titre ou d'un portefeuille.
- Une variance élevée indique une incertitude et un risque plus importants associés à l'investissement, tandis qu'une variance faible indique un risque moindre.
- Les traders et les investisseurs utilisent la variance pour déterminer la taille optimale d'une position pour un trade et pour diversifier leurs portefeuilles afin de gérer le risque.
Formule de variance
La formule de variance est une expression mathématique qui calcule la dispersion ou la variabilité d'un ensemble de points de données.
Elle est définie comme la moyenne des différences au carré entre chaque point de données et la moyenne de l'ensemble.
La formule de la variance est la suivante :
Variance = Σ (xi - μ)² / n
où :
- Σ est le symbole de sommation (signifiant "somme de").
- xi est la valeur du ième point de données dans l'ensemble
- μ est la valeur moyenne de l'ensemble.
- n est le nombre total de points de données dans l'ensemble.
Pour calculer la variance, vous devez d'abord calculer la moyenne de l'ensemble des données.
Ensuite, pour chaque point de données, il faut soustraire la moyenne du point de données, élever la différence au carré et l'ajouter à la somme.
Enfin, vous divisez la somme par le nombre total de points de données pour obtenir la variance.
La formule de variance est utilisée dans de nombreux calculs statistiques, tels que les tests d'hypothèse, l'analyse de régression et le contrôle de la qualité.
C'est également un élément clé du calcul d'autres mesures statistiques, comme l'écart-type, qui est la racine carrée de la variance.
Comment la variance est-elle utilisée dans le trading ?
Dans le trading, la variance est souvent utilisée pour déterminer la taille optimale d'une position pour un trade.
En comprenant la variance attendue d'un titre ou d'un portefeuille, les traders peuvent déterminer le montant du risque qu'ils sont prêts à prendre et ajuster la taille de leur position en conséquence.
Par exemple, si la variance est élevée, un trader peut décider de réduire la taille de sa position pour limiter les pertes potentielles.
Dans la gestion de portefeuille, la variance joue un rôle clé dans la diversification.
Un portefeuille bien diversifié comprendra des actifs présentant différents niveaux naturels de variance, ce qui permet de réduire le risque global du portefeuille.
En combinant ces types d'actifs, les investisseurs peuvent créer un portefeuille qui atteint le niveau de risque souhaité tout en maximisant les rendements.
Dans l'ensemble, la variance est une mesure essentielle pour les investisseurs et les traders, car elle les aide à comprendre le niveau de risque associé à un investissement et à prendre des décisions éclairées sur la gestion du portefeuille et les stratégies de trading.
Variance et écart-type
La variance et l'écart-type sont tous deux des mesures de la variabilité ou de la dispersion d'un ensemble de données.
Cependant, l'écart-type est plus couramment utilisé dans le trading et les investissements, car il sert à mesurer la volatilité.
Variance
La variance est une mesure statistique de l'écart entre les points de données d'un ensemble et la moyenne de cet ensemble.
Elle est calculée en trouvant la moyenne des différences au carré entre chaque point de données et la moyenne de l'ensemble.
Une variance plus élevée indique que les points de données sont plus dispersés et plus éloignés de la moyenne.
Écart-type
L'écart-type, quant à lui, est la racine carrée de la variance.
Il s'agit d'une mesure de l'écart entre les points de données et la moyenne de l'ensemble. L'écart-type est souvent utilisé dans le trading et l'investissement pour mesurer la volatilité d'une action ou d'un portefeuille.
Un écart-type plus élevé indique que les rendements de l'action ou du portefeuille sont plus volatils ou plus risqués.
Dans le trading et l'investissement, il est important de comprendre la variabilité des rendements car elle peut indiquer le niveau de risque associé à un investissement particulier.
Par exemple, un investisseur peut préférer une action dont l'écart-type est faible, car elle est moins volatile et offre un rendement plus stable dans le temps.
Cependant, un écart-type plus élevé peut être préféré par un investisseur plus tolérant au risque qui est prêt à accepter une plus grande volatilité en échange de rendements potentiellement plus élevés.
C'est à ce moment-là que les traders/investisseurs commencent à parler de choses comme les "rendements ajustés au risque" ou les ratios tels que Sharpe, Sortino, Treynor, et d'autres formes de mesure du rendement ajusté au risque.
Dans l'ensemble, l'écart-type est une mesure plus utile dans le trading et l'investissement, car il permet une compréhension plus intuitive de la variabilité des rendements, et il est largement utilisé dans les modèles et analyses financiers.
Types de variance en statistiques
En statistique, la variance est une mesure de la dispersion d'un ensemble de données. Il existe plusieurs types de variance qui sont couramment utilisés dans l'analyse statistique.
Voici quelques-uns des types de variance les plus courants :
Variance de la population
La variance de la population est la variance d'une population entière.
Elle mesure la dispersion des données dans la population.
Variance de l'échantillon
La variance de l'échantillon est la variance d'un échantillon de données.
Elle est utilisée pour estimer la variance de la population.
Comme l'échantillon est généralement plus petit que la population, la variance de l'échantillon sera différente de la variance de la population.
Variance intra-groupe
La variance intra-groupe est la variance au sein d'un groupe de données.
Elle est utilisée dans l'analyse de la variance (ANOVA) pour déterminer s'il existe des différences significatives entre les groupes.
Variance entre groupes
La variance entre les groupes est la variance entre les groupes de données.
Elle est également utilisée dans l'ANOVA pour déterminer s'il existe des différences significatives entre les groupes.
Variance résiduelle
La variance résiduelle est la variance qui subsiste après l'ajustement d'un modèle aux données. Elle mesure la mesure dans laquelle le modèle est capable d'expliquer la variabilité des données.
Chacun de ces types de variance a une utilisation spécifique dans l'analyse statistique. Il est important de choisir le type de variance approprié pour l'analyse que vous effectuez afin de garantir des résultats précis et significatifs.
Variance et covariance
La variance et la covariance sont deux concepts importants en trading et en finance, car ils permettent de quantifier la volatilité et la corrélation des actifs d'un portefeuille.
La variance mesure la variabilité des rendements d'un seul actif, tandis que la covariance mesure la variabilité conjointe des rendements de deux actifs.
Dans le trading, la variance est souvent utilisée pour mesurer la volatilité, ou le degré de variation des rendements d'un actif dans le temps.
La volatilité est un facteur important pour les traders, car elle affecte le risque et la récompense potentielle d'un investissement.
Une variance plus élevée indique un plus grand degré de volatilité et de risque, tandis qu'une variance plus faible indique une volatilité et un risque moindres.
La covariance, quant à elle, mesure la façon dont deux actifs évoluent ensemble. Une covariance positive indique que les deux actifs ont tendance à évoluer dans la même direction, tandis qu'une covariance négative indique qu'ils ont tendance à évoluer dans des directions opposées.
La covariance est importante pour les traders car elle les aide à diversifier leur portefeuille en identifiant les actifs qui ne sont pas fortement corrélés entre eux. Cela peut contribuer à réduire le risque global et à augmenter les rendements potentiels.
En résumé, la variance mesure la volatilité d'un seul actif, tandis que la covariance mesure la corrélation entre deux actifs. Ces deux concepts sont importants dans le trading et la finance et peuvent être utilisés pour gérer le risque et augmenter les rendements potentiels d'un portefeuille.
Compromis moyenne-variance
Le compromis moyenne-variance est un concept fondamental en finance qui fait référence au compromis entre le rendement attendu et le risque (ou variance) d'un investissement.
En d'autres termes, les investisseurs ont le choix entre prendre plus de risques pour obtenir des rendements potentiellement plus élevés ou accepter des rendements plus faibles en échange d'un niveau de risque plus faible.
Dans le contexte du trading et de l'investissement, le compromis moyenne-variance est souvent utilisé pour construire des portefeuilles qui optimisent l'équilibre entre risque et rendement.
La théorie moderne du portefeuille, développée par Harry Markowitz, fournit un cadre pour déterminer le portefeuille optimal qui permet d'obtenir le rendement attendu le plus élevé pour un niveau de risque donné.
Cette théorie part du principe que les investisseurs ont une aversion pour le risque et préfèrent les portefeuilles qui minimisent le risque pour un niveau de rendement donné ou qui maximisent le rendement pour un niveau de risque donné.
En pratique, les investisseurs utilisent des outils tels que le modèle d'évaluation des actifs financiers (MEDAF) et la frontière efficiente pour identifier l'allocation optimale du portefeuille.
Le MEDAF utilise le rendement attendu du marché, le taux sans risque et le bêta du titre pour calculer le rendement attendu d'un actif, tandis que la frontière efficiente identifie l'ensemble des portefeuilles qui offrent le rendement attendu le plus élevé pour un niveau de risque donné.
Les investisseurs doivent tenir compte du compromis moyenne-variance afin de prendre des décisions d'investissement éclairées.
Les investissements à haut risque et à haut rendement peuvent convenir à certains investisseurs, tandis que d'autres préfèrent les investissements à faible risque et à faible rendement.
Un portefeuille bien diversifié qui comprend une combinaison d'actifs présentant différents niveaux de risque peut aider à atteindre un équilibre plus optimal entre le risque et le rendement.
Variance et valeur attendue
Dans le trading et l'investissement, la variance et la valeur attendue sont deux concepts importants qui aident les investisseurs à prendre des décisions éclairées concernant leurs investissements.
La valeur attendue (VA) est une mesure du résultat moyen d'un investissement particulier ou d'une stratégie de trading.
Elle représente la somme des résultats pondérés par les probabilités de tous les scénarios possibles.
Par exemple, si un investisseur a 60 % de chances d'obtenir un rendement de 10 % sur un investissement et 40 % de chances de perdre 5 %, la valeur attendue de l'investissement est la suivante
- (0,6 * 0,10) + (0,4 * -0,05) = 0,06 - 0,02 = 0,04, soit un rendement attendu de 4 %.
La variance mesure la dispersion ou l'écart des résultats possibles autour de la valeur attendue.
Une variance élevée indique que le résultat réel est susceptible de s'écarter considérablement de la valeur attendue, tandis qu'une variance faible indique que le résultat réel est susceptible d'être proche de la valeur attendue.
En d'autres termes, la variance est une mesure du risque associé à un investissement ou à une stratégie de trading.
Par exemple, si deux investissements ont le même rendement attendu de 10 %, mais que l'un a une variance élevée et l'autre une variance faible, l'investissement à variance élevée est plus risqué car ses rendements réels seront probablement plus dispersés et imprévisibles.
Les investisseurs et les traders utilisent à la fois la valeur attendue et la variance pour évaluer et comparer les opportunités d'investissement.
Ils peuvent préférer les investissements dont la valeur attendue est élevée et la variance faible, ce qui indique que l'investissement a le potentiel de générer des rendements importants tout en étant relativement prévisible.
Cependant, certains investisseurs peuvent être prêts à prendre un risque plus élevé et à accepter une variance plus importante pour obtenir des rendements plus élevés.
Exemple ludique de la variance par rapport à la valeur attendue
Disons que vous jouez à un jeu avec trois options :
- Option 1 : 80 % de chances de gagner 10 000 $.
- Option 2 : 30 % de chances de gagner 100 000 $.
- Option 3 : 10% de chances de gagner 1 000 000 $.
Vos valeurs attendues dans chaque situation sont
- 8,000 $
- 30,000 $
- 100,000 $
Sacrifieriez-vous la VA pour une variance plus faible ?
Elle peut être parfaitement raisonnable.Le type de personne qui choisirait chaque option en fonction de sa tolérance au risque et de sa situation financière varierait en fonction de ses préférences individuelles, de ses objectifs financiers et de son attitude face au risque.
Option 1
Une personne qui a une aversion pour le risque et une faible capacité de risque financier peut choisir l'option 1 parce qu'elle offre une plus grande probabilité de gagner, bien que la récompense soit moindre.
Cette personne peut privilégier la sécurité d'un gain plus garanti et être prête à sacrifier la possibilité de gagner une plus grosse somme d'argent pour éviter le risque de tout perdre.
Option 2
Une personne dont le niveau de tolérance au risque est modéré et dont la capacité à prendre des risques financiers est plus élevée peut choisir l'option 2 parce qu'elle offre une récompense potentielle plus élevée en contrepartie d'une prise de risque plus importante.
Cette personne peut être prête à accepter une probabilité de gain plus faible en échange de la possibilité de gagner une somme d'argent plus élevée.
Toutefois, cette personne peut vouloir limiter son exposition au risque et ne pas être prête à tout risquer pour avoir une chance de gagner une grosse somme d'argent.
Option 3
Une personne qui tolère bien le risque et qui a une grande capacité de risque financier peut choisir l'option 3 parce qu'elle offre la récompense potentielle la plus élevée, même si la probabilité de gagner est la plus faible.
Cette personne peut être prête à prendre un niveau de risque plus élevé en échange de la possibilité de gagner une somme d'argent beaucoup plus importante.
Cependant, cette personne doit être prête à accepter le risque de tout perdre pour avoir une chance de gagner une somme beaucoup plus importante.
Il convient de noter qu'il ne s'agit là que de généralisations et que la tolérance au risque et la situation financière des personnes peuvent varier considérablement en fonction de leur situation personnelle, de leurs objectifs financiers et de leur psychologie.
Comment concevriez-vous ce jeu pour obtenir un tiers d'un échantillon statistiquement significatif pour chaque option ?
Cela nécessiterait des essais et des erreurs.
Vous aurez besoin d'un nombre suffisant de participants pour garantir la signification statistique et d'un échantillon véritablement aléatoire.
Par exemple, si vous choisissez des jeunes diplômés de l'enseignement supérieur, vous pouvez parier qu'ils voteront majoritairement pour la première option, car une probabilité de 80 % d'avoir 10 000 dollars a plus de valeur pour eux que de se lancer dans un pari sur une somme plus importante qu'ils risquent de ne pas avoir.
D'un autre côté, si votre échantillon est composé de gens d'affaires prospères, la première option pourrait être sous-représentée parce que 10 000 $ ne sont peut-être pas si importants pour eux.
Si vous disposiez d'un échantillon aléatoire avec un nombre statistiquement significatif de votes et que vous constatiez que l'option 1 domine, vous pourriez modifier le jeu de la manière suivante :
- Option 1 : 80 % de chances de gagner 10 000 $.
- Option 2 : 50 % de chances de gagner 100 000 $.
- Option 3 : 20 % de chances de gagner 1 000 000 $.
Vos valeurs attendues dans chaque situation seraient alors les suivantes :
- 8,000 $
- 50,000 $
- 200,000 $
Ce processus d'essai et d'erreur est analogue à la façon dont les marchés fonctionnent dans le monde réel.
Le "prix de compensation" serait celui qui recueille un tiers des votes sur chacun.
Sur les marchés financiers, cela pourrait être analogue au fait de posséder des bons du Trésor sûrs plutôt que des actions ou des formes de crédit plus risquées plutôt que du capital-risque.
Plus on monte dans l'échelle des risques, plus la valeur attendue est élevée, mais au prix d'une plus grande variance ou d'un risque plus élevé de perte ou d'échec.
Variance - clairement expliquée
FAQs - Variance
La variance est-elle la même chose que la volatilité ?
La variance et la volatilité sont des concepts liés, mais ce n'est pas exactement la même chose.
La variance est une mesure statistique qui quantifie la dispersion d'un ensemble de points de données autour de la moyenne.
Elle est calculée comme la moyenne des différences au carré par rapport à la moyenne.
En finance, la variance est souvent utilisée pour mesurer le risque d'un portefeuille ou d'un titre individuel.
La volatilité, quant à elle, est une mesure du degré de variation du prix d'un instrument financier dans le temps.
Elle peut être calculée à l'aide de différentes méthodes, mais une approche courante consiste à utiliser l'écart type des rendements de l'instrument sur une période donnée.
La volatilité est souvent utilisée comme un indicateur du risque (ou d'une composante du risque), car une volatilité plus élevée implique un plus grand degré d'incertitude ou un potentiel de mouvements de prix importants.
En finance, la volatilité et la variance sont souvent utilisées de manière interchangeable, mais ce n'est pas exactement la même chose.
La variance est un concept mathématique qui sert souvent de base au calcul de la volatilité, mais la volatilité est une mesure plus spécifique qui prend en compte les séries chronologiques de prix ou de rendements.
Quel est le compromis biais-variance ?
Le compromis biais-variance est un concept fondamental de l'apprentissage automatique qui fait référence au compromis entre la capacité d'un modèle à bien s'adapter aux données d'apprentissage (faible biais) et sa capacité à généraliser à de nouvelles données non vues (faible variance).
Le biais est la différence entre les valeurs prédites d'un modèle et les valeurs réelles des données.
Un modèle présentant un biais élevé est généralement trop simplifié et ne peut pas saisir la complexité des données, ce qui entraîne un sous-ajustement.
En d'autres termes, le modèle n'est pas en mesure d'apprendre les modèles sous-jacents des données et ses prédictions sont systématiquement fausses.
La variance est la variabilité des prédictions du modèle pour différents ensembles de données d'apprentissage.
Un modèle avec une variance élevée est généralement trop complexe et a surajusté les données d'apprentissage, ce qui se traduit par un modèle qui n'est pas en mesure de bien généraliser à de nouvelles données.
En d'autres termes, le modèle a mémorisé les données d'apprentissage et est incapable d'appliquer ce qu'il a appris à de nouvelles données.
L'objectif de l'apprentissage automatique est de trouver le compromis optimal entre le biais et la variance, en sélectionnant un modèle suffisamment complexe pour capturer les modèles sous-jacents des données, mais pas trop complexe au point de sur-appliquer les données d'apprentissage.
On peut y parvenir en sélectionnant une complexité de modèle appropriée, en utilisant des techniques de régularisation pour pénaliser les modèles complexes, ou en utilisant des méthodes d'ensemble pour combiner plusieurs modèles avec des biais et des variances différents.
Qu'est-ce qu'un swap de variance ?
Un swap de variance est un contrat financier qui permet aux investisseurs de parier sur le niveau de volatilité du prix d'un actif sous-jacent, comme une action, un indice ou une marchandise.
Le contrat est généralement structuré comme un produit dérivé de gré à gré (OTC) et implique un paiement basé sur la différence entre la variance réalisée du prix de l'actif sur une période de temps donnée et un niveau de variance convenu à l'avance, appelé variance d'exercice.
Dans un swap de variance, l'acheteur accepte de payer un montant fixe au vendeur en échange d'un paiement basé sur la différence entre la variance réalisée et la variance d'exercice.
Si l'écart réalisé est supérieur à l'écart d'exercice, le vendeur effectuera un paiement à l'acheteur, et vice versa.
Les swaps de variance sont couramment utilisés par les investisseurs qui souhaitent avoir un avis sur la volatilité d'un actif, plutôt que sur sa direction.
Ils peuvent être utilisés à des fins de couverture ou de spéculation, et sont souvent utilisés par les teneurs de marché et les investisseurs institutionnels.
Les swaps de variance peuvent être personnalisés pour répondre aux besoins spécifiques de l'acheteur et du vendeur, tels que l'actif sous-jacent, la variance d'exercice et la durée du contrat.
Conclusion - Variance
La variance est une mesure statistique qui quantifie l'écart ou la dispersion d'un ensemble de points de données autour de leur moyenne ou de leur valeur attendue.
Dans le trading et l'investissement, la variance est un concept important qui aide les participants au marché à comprendre le risque associé à leurs investissements.
Une variance élevée indique que les rendements réels sont susceptibles de s'écarter considérablement de la valeur attendue, ce qui rend l'investissement plus risqué, tandis qu'une variance faible indique que les rendements réels sont susceptibles d'être plus proches de la valeur attendue, ce qui rend l'investissement moins risqué.
Les investisseurs utilisent la variance pour évaluer et comparer les opportunités d'investissement et pour prendre des décisions éclairées concernant leurs portefeuilles.