L'importance de la valeur attendue dans le trading
Chaque décision que vous prenez sur les marchés financiers doit être formulée comme un calcul de la valeur attendue.
Chaque trade ou chaque pari peut être considéré comme une probabilité. Il existe une probabilité et une récompense pour avoir raison et une probabilité et une pénalité pour avoir tort.
En d'autres termes, la façon de calculer la valeur attendue peut être expliquée comme suit :
Valeur attendue = P(correct) * R(correct) - P(incorrect) * R(incorrect)
- P = probabilité
- R = récompense
En général, un trade gagnant aura une valeur attendue positive, c'est-à-dire que la valeur de la probabilité d'avoir raison multipliée par la récompense pour avoir raison dépasse la probabilité d'avoir tort multipliée par la récompense pour avoir tort. Un trade perdant aura une valeur attendue négative.
Les traders veulent maximiser leur valeur attendue.
Principaux points à retenir - Valeur attendue
La valeur attendue est un concept statistique qui peut être appliqué au trading. Voici trois points clés à retenir pour expliquer ce concept :
- La valeur attendue est le résultat moyen d'une stratégie de trading sur de nombreux trades. Elle prend en compte la probabilité de chaque résultat et l'ampleur du résultat, positif ou négatif.
- Une valeur attendue positive indique qu'une stratégie de trading devrait gagner de l'argent sur le long terme, tandis qu'une valeur attendue négative indique qu'une stratégie de trading devrait perdre de l'argent sur le long terme.
- En calculant la valeur attendue d'une stratégie de trading, les traders peuvent évaluer si la stratégie est susceptible d'être rentable ou non, et prendre des décisions éclairées sur la gestion des risques et le dimensionnement des positions. Cependant, il est important de noter que la valeur attendue n'est pas une garantie des résultats futurs et que les résultats réels du trading peuvent différer de la valeur attendue.
Exemples de valeur attendue
Examinons quelques exemples d'exercices.
Exemple nº 1
Supposons que la probabilité d'avoir raison soit de 70 % et que la récompense pour avoir raison soit de 50 $, et que la probabilité d'avoir tort soit de 30 % et que la récompense pour avoir tort soit de 100 $ (ou -100 $ pour indiquer la perte d'argent).
Est-il judicieux de prendre ce pari ?
En suivant la formule :
- VA = 0,70 * 50 $ + 0,30 * -100 $ = 35 $ - 30 $ = +5 $.
Étant donné que la valeur attendue est positive - si vous avez évalué correctement vos probabilités - la récompense attendue est supérieure à la pénalité attendue. Ce pari peut être viable tant que vous pouvez couvrir la perte (-100 $) en cas d'erreur.
Exemple n° 2
En comprenant la valeur attendue, vous pouvez également observer qu'il n'est pas judicieux de parier uniquement sur ce qui est le plus probable.
Par exemple, sur les marchés, vous serez souvent confronté à des situations où la probabilité d'avoir raison est assez élevée, mais où la récompense est faible et la pénalité pour avoir tort est en conséquence élevée.
La vente d'options non couvertes en dehors du cours (OTM) en est un exemple courant. Beaucoup vendront des options OTM en pensant que leurs chances d'avoir raison sont élevées et que cela rend le pari favorable.
Cependant, le calcul réel des profits et des pertes est souvent très différent.
Si vous avez 90 % de chances d'avoir raison et que votre récompense est de 20 $, mais que vous avez 10 % de chances d'avoir tort et que la pénalité est de 1 000 $, la réalité peut être un peu différente :
- VA = 0,90 * 20 $ + 0,10 * 1 000 $ = -80 $.
Dans ce cas, vous pouvez avoir un pourcentage de gain élevé, mais si vous ne faites pas de paris à valeur attendue positive, vous perdrez de l'argent. Et si vous ne pouvez pas couvrir la perte attendue, il y a l'élément "risque de ruine".
Lorsque les gens ruinent leurs comptes de trading, c'est généralement en raison d'un effet de levier excessif, en misant trop sur un pari donné dans un style tout ou rien, ou en vendant des options.
La gestion du risque est essentielle en toute circonstance.
Exemple n° 3
En revanche, si vos chances d'avoir raison sont faibles mais que la récompense est élevée, et si vos chances d'avoir tort sont élevées mais que le coût de cette erreur est négligeable, il peut être judicieux de le faire.
Disons que vous avez 99 % de chances de vous tromper mais que le coût de cette erreur est de 100 $, et que vous avez 1 % de chances d'avoir raison mais que votre récompense est de 100 000 $.
Il peut s'agir d'un pari sur les marchés financiers ou de l'envoi d'une demande d'emploi supplémentaire et de la possibilité de passer un entretien d'embauche, ce qui prend peu de temps et n'entraîne pas de perte d'opportunités ailleurs, mais offre une récompense tangible si vous réussissez, sous la forme d'un salaire de qualité, d'avantages sociaux et d'autres avantages.
- VA = 0,01 * 100 000 $ + 0,99 * -100 $ = +901 $
Votre récompense est 1 000 fois plus élevée que ce qu'il vous en coûte si vous vous trompez ou si vous échouez et que vous estimez que vos chances sont telles qu'il est logique de tenter votre chance, même si les chances sont apparemment très défavorables.
Si vous pouvez vous permettre d'assumer le coût de l'erreur et que vous avez évalué vos chances avec précision, alors la décision est très raisonnable.
Dans le trading, le concept est similaire. Si vous faites des paris à valeur attendue positive de manière répétée, vous obtiendrez des résultats rentables au fil du temps.
Certaines stratégies qui se concentrent sur les événements extrêmes peuvent être extrêmement rentables dans de rares cas (par exemple, la crise financière de 2008, la pandémie de Covid-19 en 2020) et ne perdre que très peu dans la plupart des autres environnements.
Mark Spitznagel, directeur d'Universa Investments, a saisi cette idée lorsque son entreprise a gagné plus de 4 000 % en se couvrant pendant la crise de Covid-19 :
"Lorsque le marché s'effondre, je veux gagner beaucoup, et lorsque le marché ne s'effondre pas, je veux perdre un tout petit montant. Je veux cette asymétrie... cette convexité."
Si vous perdez de l'argent et que vous le faites sur une taille d'échantillon qui rend probable que vous n'êtes pas simplement confronté aux caprices du marché, alors vous devez vraiment évaluer si la stratégie (ou les stratégies) que vous utilisez met les chances de votre côté.
Il est important de résister à la tentation de croire que perdre de l'argent signifie que la chance n'est pas de votre côté.
Exemple n° 4
Si vous jouiez à un jeu de pile ou face où vous pouviez parier sur pile ou face, chacune ayant une chance égale de se révéler correcte, risqueriez-vous 100 $ pour gagner 199 $ si vous aviez raison (la mise initiale de 100 $ est remboursée plus 99 $ en plus) et perdriez-vous la totalité des 100 $ si vous aviez tort ?
En suivant la formule :
- VA = 0,50 * 99 $ + 0,5 * -100 $ = - 0,50 $.
Donc, la réponse devrait être non.
La valeur attendue n'est que légèrement négative, donc votre marge ne semble pas mauvaise.
Cependant, si vous jouez à ce jeu 200 fois avec une mise égale de 100 $ à chaque fois, vous vous attendez à perdre 100 $ (200 multiplié par la perte attendue de - 0,50 $), soit l'équivalent de votre mise habituelle.
Néanmoins, il y a encore 36,7 % de chances* que vous soyez rentable après 200 tours de ce jeu. (Il faudrait 919 tours pour que vos chances d'être rentable tombent à moins de 1 %).
* Ce chiffre est calculé en prenant le gain attendu par pari, en prenant la différence relative au montant misé par pari, et en divisant par le montant misé par pari. Puis on le prend à la puissance du nombre de tours joués :
- [($100 + -$0.50) / $100]^200 = ($99.5/$100)^200 = .995^200 = .367 = 36.7%
Cela peut prendre un certain temps avant d'apprendre que vous avez une mauvaise stratégie si vous êtes juste à la limite entre quelque chose de viable et pas mieux que de jouer à pile ou face.
Exemple n° 5 - La roulette américaine
Sur une roulette américaine, il y a 38 numéros, 18 rouges, 18 noirs et 2 verts.
Si vous pariez 10 $ sur le rouge 10 fois de suite, quelles sont vos chances de gagner de l'argent ?
Si vous avez raison, vous gagnez 20 $ (le double de votre mise), tandis que si vous vous trompez, vous perdez tout.
Il y a 18 poches rouges et 38 poches au total, donc votre valeur attendue par tour serait :
- VA = 18/38 * 20 $ + 20/38 * 10 $ = 9,47 $.
Cela représente une perte attendue de 0,53 $ par tour (10 $ moins la valeur attendue).
Quelles sont les chances de perdre de l'argent après 10 tours ?
La probabilité de perdre de l'argent après 10 tours, en supposant que vous faites des paris d'argent pair à chaque tour, peut être calculée en utilisant la distribution binomiale, qui est une formule mathématique décrivant la probabilité d'un certain nombre de succès dans un nombre fixe d'essais.
En supposant que vous commencez avec une certaine somme d'argent et que vous voulez connaître la probabilité que vous vous retrouviez avec moins que cette somme après 10 tours de paris à somme égale, la probabilité de perdre de l'argent peut être calculée comme suit :
- P(perte) = Σ (i = 0 à 10) (10 choisir i) * (47,37%)^i * (52,63%)^(10-i)
Où "i" représente le nombre de tours que vous gagnez, "10 choisir i" représente le nombre de façons de choisir "i" tours gagnants sur 10, et (47,37%)^i et (52,63%)^(10-i) représentent la probabilité de gagner "i" tours et de perdre (10-i) tours, respectivement.
À l'aide d'une calculatrice ou d'un logiciel statistique, on peut évaluer cette équation et constater que la probabilité de perdre de l'argent après 10 tours de mise à parité à la roulette américaine est d'environ 87,9 %.
Par conséquent, les chances de perdre de l'argent après 10 tours de mise égale à chaque tour à la roulette américaine sont assez élevées.
Les chances de perdre de l'argent après 100 tours ?
Si vous continuez à faire des paris d'argent pair pendant 100 tours de roulette américaine, la probabilité de perdre de l'argent peut être calculée de la même manière en utilisant la distribution binomiale.
La probabilité de perdre de l'argent après 100 tours peut être calculée comme suit :
- P(perte) = Σ (i = 0 à 100) (100 choisir i) * (47,37%)^i * (52,63%)^(100-i)
À l'aide d'une calculatrice ou d'un logiciel statistique, on peut évaluer cette équation pour trouver que la probabilité de perdre de l'argent après 100 tours de mise à parité à la roulette américaine est d'environ 99,8 %.
Exemple n° 6 - Roulette européenne
La roulette européenne est similaire à la roulette américaine, mais avec une différence essentielle : elle ne comporte qu'une seule poche 0, alors que la roulette américaine comporte à la fois des poches 0 et 00. Cela signifie que les chances de gagner une mise égale à la roulette européenne sont légèrement meilleures que celles de la roulette américaine, car il y a une poche de moins qui donne un avantage à la maison.
En supposant que vous faites des mises paires (par exemple, en misant sur le rouge ou le noir, l'impair ou le pair, le haut ou le bas), les chances de gagner une mise individuelle à la roulette européenne sont de 18/37, soit environ 48,65 %. Les chances de perdre un pari individuel sont donc d'environ 51,35 %.
Ainsi, votre VA lorsque vous pariez sur le rouge ou le noir est :
- VA = 18/37 * 20 $ + 19/37 * 10 $ = 9,73 $.
Vous devez donc vous attendre à perdre 0,27 $ par tour.
Vos chances de gagner de l'argent sur 10 essais sont :
- 1 - ($9.73/$10)^10 = 1 - 0.973^10 = 1 - 0.58 = 0.42 = 42%
Pour calculer la probabilité de perdre de l'argent après un certain nombre de tours de mise égale à chaque tour, nous pouvons utiliser la même formule de distribution binomiale que pour la roulette américaine.
En supposant 10 tours de mise égale à la roulette européenne, la probabilité de perdre de l'argent peut être calculée comme suit :
- P(perte) = Σ (i = 0 à 10) (10 choisir i) * (48,65%)^i * (51,35%)^(10-i)
À l'aide d'une calculatrice ou d'un logiciel statistique, cette équation peut être évaluée pour déterminer que la probabilité de perdre de l'argent après 10 tours de mise à parité à la roulette européenne est d'environ 83,22 %.
Si l'on suppose 100 tours de paris à somme égale sur la roulette européenne, la probabilité de perdre de l'argent peut être calculée comme suit :
- P(perte) = Σ (i = 0 à 100) (100 choisir i) * (48,65%)^i * (51,35%)^(100-i)
À l'aide d'une calculatrice ou d'un logiciel statistique, on peut évaluer cette équation pour trouver que la probabilité de perdre de l'argent après 100 tours de mise à parité à la roulette européenne est d'environ 94,40 %.
Par conséquent, les chances de perdre de l'argent après 100 tours de mise égale à chaque tour à la roulette européenne sont encore assez élevées, mais légèrement inférieures aux chances de perdre de l'argent à la roulette américaine.
Est-il toujours préférable de se concentrer uniquement sur la valeur attendue ?
Non, faire un trade ou une décision à valeur attendue positive (ou le trade ou la décision à VA la plus élevée) n'est pas toujours le meilleur choix.
Voici quelques raisons pour lesquelles :
Gestion du risque
Un trade ou une décision à valeur attendue positive peut néanmoins comporter un risque important.
Les traders doivent prendre en compte non seulement la valeur attendue d'un trade mais aussi le risque potentiel de baisse, y compris la possibilité d'une perte importante.
La gestion du risque est une partie importante de toute stratégie de trading, et les traders doivent être capables d'identifier et de gérer le risque pour minimiser les pertes potentielles.
Si vous avez un avantage connu de 51/49 sur quelque chose et que vous pouvez parier 10 $ dessus encore et encore, vous le ferez toujours si vous le pouvez. Cependant, vous ne voulez pas y engager une somme d'argent importante car vous pouvez perdre plusieurs situations 51/49 d'affilée.
Coût d'opportunité
Même si un trade a une valeur attendue positive, il peut ne pas être la meilleure utilisation du capital d'un trader.
S'il existe d'autres opportunités de trading offrant un meilleur ratio risque/récompense ou des profits potentiels plus élevés, un trader peut choisir de saisir ces opportunités au lieu du trade à valeur attendue positive.
Situations de valeur attendue positive avec une variance plus faible
Disons que vous jouez à un jeu avec trois options :
- Option 1 : 80 % de chances de gagner 10 000 $.
- Option 2 : 20 % de chances de gagner 100 000 $.
- Option 3 : 5% de chances de gagner 1 000 000 $.
Vos valeurs attendues dans chaque situation sont
- 8,000 $
- 20,000 $
- 50,000 $
Que choisiraient la plupart des gens dans cette situation ?
Ce que la plupart des gens choisiraient dans cette situation dépend de divers facteurs, dont leur tolérance au risque, leur situation financière et leurs objectifs généraux.
Voici quelques scénarios possibles :
- Risque élevé, récompense élevée : Certaines personnes peuvent être prêtes à prendre plus de risques en échange d'une chance d'obtenir une récompense élevée. Pour ces personnes, l'option 3 (5 % de chances de gagner 1 000 000 $) peut être la plus attrayante, malgré une probabilité de gain plus faible. Elles peuvent être prêtes à accepter des chances plus faibles en échange d'une petite chance d'obtenir un gain très important et de l'option à la valeur attendue la plus élevée.
- Risque modéré, récompense modérée : D'autres personnes peuvent être plus réticentes au risque et préfèrent adopter une approche plus modérée. Dans ce cas, l'option 2 (20 % de chances de gagner 100 000 $) peut être plus attrayante. Bien que la valeur attendue soit inférieure à celle de l'option 3, la probabilité de gagner est plus élevée, ce qui en fait une option risque-récompense plus modérée.
- Faible risque, faible récompense : Pour les personnes qui ont une forte aversion au risque ou des ressources financières limitées, l'option 1 (80 % de chances de gagner 10 000 $) peut être la plus attrayante. Bien que la valeur attendue soit inférieure à celle des options 2 et 3, la probabilité de gagner est beaucoup plus élevée, ce qui en fait une option plus sûre avec une récompense plus modeste.
Sur les marchés, cela pourrait être analogue au choix entre des obligations sûres, des actions ou des investissements spéculatifs en démarrage.
Les probabilités sont dynamiques et souvent inconnues
Les probabilités ne sont souvent pas connues explicitement et elles sont rarement statiques.
Le marché peut être imprévisible, et des facteurs tels que des nouvelles inattendues ou des changements dans le sentiment du marché peuvent rapidement modifier la valeur attendue d'un trade.
Les traders doivent être capables de s'adapter aux conditions changeantes du marché et d'ajuster leurs stratégies en conséquence.
Coûts du trading
Réaliser un trade à valeur attendue positive ne garantit pas un profit, car les coûts de trading tels que les commissions, les frais et les spreads peuvent réduire les profits potentiels.
Les traders doivent tenir compte de ces coûts lorsqu'ils calculent la valeur attendue d'un trade et adapter leurs stratégies en conséquence.
En résumé, bien que les trades ou les décisions à valeur attendue positive soient généralement privilégiés, les traders doivent tenir compte d'autres facteurs tels que la gestion des risques, le coût d'opportunité, les conditions du marché et les coûts de trading lorsqu'ils prennent leurs décisions. Le trading est un processus complexe et dynamique, et les traders doivent être capables de s'adapter aux conditions changeantes du marché et de prendre des décisions éclairées en fonction de divers facteurs.
Valeur attendue dans le trading d'options
La valeur attendue est souvent utilisée dans le trading d'options, en particulier.
De nombreux traders apprécient les options car elles leur permettent de saisir une partie spécifique de la distribution des résultats potentiels. Cela signifie qu'ils peuvent adapter plus soigneusement leurs idées de trading et leurs thèses d'investissement pour exprimer certains points de vue.
Pour savoir si un trade vaut la peine d'être effectué, il est important d'effectuer des calculs de valeur attendue.
Vous aurez des résultats potentiels que vous connaissez à l'avance en fonction de la façon dont vous structurez le trade.
Vous devrez ensuite attribuer des probabilités à chaque résultat pour déterminer la valeur attendue de chaque élément. En les additionnant, vous obtiendrez la valeur attendue pour l'ensemble du trade.
Brokers d'options
Exemple
Supposons que vous vouliez placer une option d'achat couverte sur une action, en prenant les échéances les plus proches dans une semaine. Par sécurité, vous voulez également limiter vos pertes en cas de baisse du cours des actions, vous achetez donc également des options de vente.
Disons que les actions se négocient à 54 $ chacune. Supposons que vous vouliez acheter 1 000 actions.
Vous vouliez maximiser la prime de risque de volatilité que vous retirez du marché, vous vendez donc des options d'achat avec un prix d'exercice de 54.
Pour être sur la défensive en cas de baisse des actions, vous achetez également des options de vente avec un prix d'exercice de 52. Cela limite vos pertes potentielles à 2 $ par action.
La structure de votre trade est essentiellement un type de collar qui ressemble au diagramme ci-dessous, avec un seuil de rentabilité qui se situe quelque part au milieu.
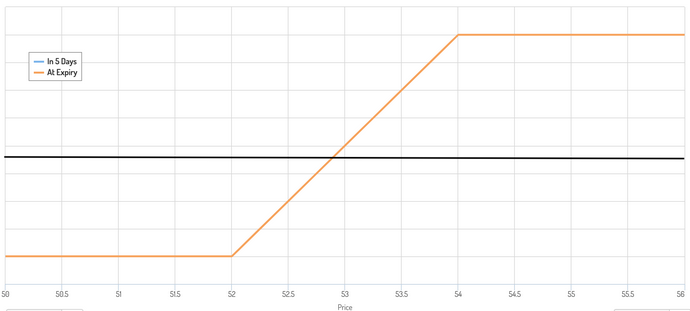
Résultats potentiels
Vous avez trois résultats catégoriques en termes de résultat final :
- Trade au-dessus de la limite supérieure du collar (c'est-à-dire au-dessus de 54 $ par action).
- Trade à l'intérieur du collar (c'est-à-dire entre 52 et 54 $ par action)
- Trade en dessous de la limite inférieure du collar (c'est-à-dire en dessous de 52 $ par action).
Étant donné que la limite supérieure du collar correspond à l'endroit où le prix se trade actuellement, être au-dessus de la limite supérieure de la bande est le plus probable de ces trois scénarios.
Comme il s'agit d'une période hebdomadaire, vos chances de terminer au-dessus de la bande sont d'environ 50 %.
Nous pouvons également dire que le trading à l'intérieur du collar (0-3,7 pour cent en dehors du cours (OTM)) a environ 33 pour cent de chances, d'après ce qu'implique le prix des options.
Certains brokers (par exemple, Interactive Brokers avec sa fonction "Probability Lab") mettent ces outils à votre disposition.
Cela signifie que le trade en dessous de la borne inférieure du collar (52$ et plus) a environ 17% de chance.
Comment calculer la valeur attendue de cette structure de trade ?
Pour calculer les valeurs attendues associées aux scénarios " au-dessus de la limite supérieure " et " au-dessous de la limite inférieure ", nous prenons simplement le coût des options et le mouvement pertinent de l'action.
Pour déterminer la valeur attendue de la catégorie intermédiaire, nous pouvons simplement prendre le point médian du prix et nous baser sur celui-ci (dans ce cas, 53 $ par action).
Gain/perte "au-dessus de la limite supérieure"
Pour la "borne supérieure supérieure", la valeur attendue est simplement le crédit que nous obtenons en vendant les 54 options d'achat.
Comme nous avons acheté 1 000 actions et qu'il y a 100 actions par contrat d'option, cela fait 10 contrats. Ils se vendaient 94 $ par contrat (0,94 $ par action), ce qui fait un total de 940 $.
Le coût des 52 options de vente était de 29 $ par contrat (0,29 $ par action), soit 290 $ au total.
Nous soustrayons les deux, 940 $ moins 290 $, ce qui donne +650 $.
Gain/perte "sous la borne inférieure"
Dans ce cas, nous obtenons toujours le bénéfice net de 650 $ des options.
Cependant, si nous descendons en dessous de 54 $, nous subissons des pertes en capital sur les actions. Le fait d'être en position longue sur les options de vente 52 limite les pertes à 2 $ par action (54 $ moins 52 $). Pour 1 000 actions, cela fait 2 000 $.
Donc, nous gagnons 650 $ de notre profit moins 2 000 $, pour une perte de 1 350 $.
Gain/perte "à l'intérieur du collar"
Dans ce cas, nous prenons le point médian (53 $ à l'expiration).
Ici, nous avons une perte en capital de 1 $ par action. Avec 1 000 actions, cela fait 1 000 $.
Nous gagnons 650 $ grâce au bénéfice net des options et soustrayons les 1 000 $ (la perte), ce qui donne une perte nette de 350 $.
Quelle est notre valeur attendue ?
Nous multiplions nos gains/pertes individuels par la probabilité qu'ils se produisent.
Nous obtenons donc :
- Au-dessus de la limite supérieure : 650 $ * 0,50 = 325 $.
- En dessous de la limite supérieure : - 1 350 $ * 0,17 = - 229,50 $.
- À l'intérieur du collar : -350 $ * 0,33 = -115,50 $.
Nous additionnons ces valeurs et obtenons moins 20 $ pour la valeur attendue.
Ainsi, si nous évaluions nos probabilités comme telles, nous n'aurions pas de valeur attendue positive.
Il serait logique que ce chiffre soit proche du seuil de rentabilité, car nous utilisons en grande partie des probabilités approximatives suggérées par le marché.
Cela illustre une autre réalité : pour gagner de l'argent sur les marchés (au-delà d'un indice de référence), il faut parier contre le consensus et avoir raison.
Si nous pensions que les probabilités associées à chacun d'entre eux étaient plutôt de 0,52, 0,15 et 0,33, alors notre valeur attendue serait positive - 20 $.
Autres facteurs dans le calcul de la valeur attendue
Il est particulièrement important d'inclure les coûts de transaction.
Il ne s'agit pas seulement du coût du trade, mais aussi de l'écart entre ce que vous tradez et la qualité de l'exécution.
Ils comprennent également les coûts de financement et/ou les frais d'emprunt.
De nombreux titres et marchés ne disposent pas de marchés d'options très liquides, ce qui signifie que l'écart est souvent assez important et qu'il y a un manque de taille au niveau des prix d'achat et de vente.
Ceci est particulièrement important pour les grandes institutions et les grands comptes, en général. Les coûts de transaction ont tendance à augmenter de manière non linéaire.
Les coûts de transaction peuvent également influencer ce que vous souhaitez trader.
Par exemple, si vous tradez des obligations de moyenne à longue durée, les contrats à terme ZB comprennent 150 000 à 200 000 $ d'obligations par contrat, selon le prix exact. Cela signifie que vous pouvez acheter un seul contrat d'option pour les ZB futures, alors que vous devez acheter environ 11 contrats pour un montant équivalent de TLT (un équivalent de l'ETF obligataire à plus longue échéance).
Les brokers facturent souvent en fonction du volume des contrats. Les prix des options sur les contrats à terme sont généralement plus élevés que ceux des options sur les actions et les ETF. Mais les contrats à terme comprennent généralement un plus grand volume du sous-jacent par contrat, ce qui peut vous aider à réduire certaines dépenses si la taille est appropriée pour votre portefeuille.
Passer de l'intuitif à l'explicite
Même si vous ne faites pas consciemment des calculs de valeur attendue, vous les faites tout le temps de manière intuitive.
Si vous avez un vol à prendre, il est probable que vous partiez pour l'aéroport bien à l'avance pour vous donner une marge de temps raisonnable.
De cette façon, il est pratiquement impossible de rater son vol en cas de problème à l'aéroport, de longues files d'attente, d'un retard à la sécurité, d'un billet ou d'un passeport égaré, ou de toute autre chose qui pourrait réduire ce délai.
Vous agissez ainsi parce que l'inconvénient de manquer un vol est élevé en termes de coût monétaire, de désagrément et/ou d'opportunité perdue.
Choisir de ne pas faire d'excès de vitesse en voiture est une autre forme de calcul de la valeur attendue. Si vos chances de recevoir une contravention pour excès de vitesse sont assez faibles si vous dépassez à peine la limite de vitesse, vous pouvez choisir de ne pas rouler du tout si le risque de recevoir une contravention est trop élevé (c'est-à-dire une amende, le temps perdu à se faire arrêter, et peut-être plus).
Le trading n'est pas différent des scénarios de la vie réelle auxquels nous sommes confrontés et que nous faisons pour maximiser notre utilité et limiter notre risque.
Prendre un risque lorsque vous avez beaucoup à gagner et très peu à perdre (par exemple, des opportunités d'emploi) ressemble beaucoup à des situations de trading où vous avez une baisse limitée et une hausse théoriquement illimitée (par exemple, l'achat d'options OTM bon marché).
De même, il est préférable de faire preuve de prudence lorsque la perte est très importante, même si les chances sont faibles (par exemple, un examen médical si vous souffrez d'un certain symptôme). Cela ressemble aux traders qui vendent des options en dehors du cours (OTM) pour une prime très faible.
Lorsque l'événement à faible probabilité se produit, ils perdent plusieurs fois la prime qu'ils avaient prévu de recevoir (parfois des centaines ou pire).
Au fur et à mesure que les traders acquièrent de l'expérience et de la sagesse, ils sont moins désireux et moins susceptibles de trader des choses pour lesquelles ils n'ont pas de fortes convictions.
Ironiquement, les traders novices ont tendance à être assez confiants et prêts à se lancer, tandis que les traders expérimentés sont ceux qui ont le plus peur de se tromper, en raison de leur exposition aux marchés au fil du temps et des inévitables épisodes douloureux qui en ont découlé.
Tous les traders doivent se lancer dans un trade en ayant conscience de la gravité de la situation et de la marge de progression dont ils disposent. C'est pourquoi certains traders choisissent de ne jamais être short gamma (ce qui signifie en gros qu'ils ne vendent jamais d'options).
Bien que cette philosophie amène certains à ne jamais profiter d'une source de rendement connue sous le nom de prime de risque de volatilité, ils savent que s'ils ne sont jamais à découvert gamma, ils ne peuvent jamais exploser. Pour certains, c'est une question de gestion prudente du risque.
Les traders ont tendance à se baser sur le passé récent pour prévoir l'avenir. Des choses peuvent se produire qui ne sont pas dans votre distribution et ne peuvent pas être évaluées.
Si quelque chose ne s'est jamais produit auparavant, la seule façon de se couvrir contre l'inconnu est d'éliminer complètement le risque de queue. Par conséquent, de nombreux traders qui sont très avancés dans la compréhension du risque et de la récompense essaieront de structurer leurs trades en utilisant des options.
S'ils vendent des options, ils les couvrent par une position sur le sous-jacent ou par une autre branche de la structure des options. En achetant des options, la gestion du risque repose entièrement sur les épaules de la contrepartie (c'est-à-dire la personne qui vous a vendu l'option).
Cela facilite également les calculs de la valeur attendue, étant donné que vous disposez d'un risque négatif clairement défini.
En outre, pour ceux qui fixent des seuils de perte, les marchés s'effondrent lorsqu'ils se ferment au trading actif pendant une certaine période ou lorsqu'il y a une dislocation, un événement important ou une donnée. Un stop-loss n'atténuera pas le risque pendant les périodes anormales.
Conclusion
Si vous êtes un trader, un joueur professionnel ou tout autre type de décideur professionnel, il est essentiel que vous connaissiez le concept de valeur attendue.
Les marchés sont similaires au poker. Vous devez constamment évaluer vos chances d'avoir raison, votre récompense pour avoir raison, les chances et la pénalité pour avoir tort, et comment évaluer ces informations avec des connaissances qui sont presque toujours imparfaites.
Pour prendre les meilleures décisions de trading, il faut bien comprendre le risque et la récompense.
Quel est votre risque, combien pouvez-vous gagner à la hausse et, très important, quelles sont les probabilités que ces choses se produisent ?
Ce n'est pas un processus facile. Pour différents traders, cela signifie différentes choses.
Certains traders veulent savoir explicitement ce qu'est leur risque de perte en ayant des options longues ou en ayant une gestion stricte du risque sous la forme d'un stop-loss.
Ils savent que deux types de risques sont sous contrôle : (1) combien ils peuvent perdre et (2) que le "risque de ruine" est impossible (ils peuvent toujours couvrir la perte).
Les meilleurs traders limitent les pertes lorsqu'ils se trompent et réalisent des bénéfices importants lorsqu'ils ont raison.
Pour utiliser une analogie avec le baseball, ce n'est pas votre moyenne à la batte qui compte (rapport entre le nombre d'at-bats réussis et le nombre total d'at-bats), mais votre pourcentage de réussite (la qualité globale des at-bats ou la quantité produite lorsque vous réussissez).
Parier sur ce qui est le plus probable n'est pas toujours la meilleure chose à faire lorsque les traders comprennent la valeur attendue.
Trop d'entre eux visent des "gains faciles" - par exemple, la vente d'options OTM - et finissent par effacer le bénéfice d'un tas de gains minuscules avec ce qui se passe quand inévitablement l'un d'entre eux se retourne contre eux, et souvent par plusieurs fois.
