Pourquoi une faible volatilité l'emporte sur une forte volatilité ?

Climax · 26-05-2024 14:28:52

Pourquoi une faible volatilité l'emporte sur une forte volatilité sur les marchés ?

L'importance du contrôle de la volatilité dans les transactions réside dans l'effet de la volatilité sur les rendements composés.

À rendement constant, une volatilité élevée réduit davantage la moyenne géométrique qu'une volatilité faible, ce qui signifie que les transactions ou les investissements à faible volatilité ont tendance à progresser plus efficacement au fil du temps.

En effet, le processus de capitalisation pénalise la forte variabilité, ce qui se traduit par des rendements à long terme plus élevés pour les investissements à faible volatilité, même si le rendement moyen est identique.

Lors de l'évaluation des transactions, des investissements ou des processus de croissance dans le temps, la moyenne géométrique est plus pertinente que la moyenne arithmétique en raison de la nature des rendements composés.

Points clés :

La raison pour laquelle une faible volatilité surpasse une forte volatilité - à moyenne arithmétique constante - réside dans les effets de la moyenne géométrique et l'influence de la capitalisation.
Une faible volatilité réduit l'impact des baisses, ce qui facilite la reprise.
Les rendements composés bénéficient de la stabilité, ce qui se traduit par une croissance à long terme plus élevée.
La diversification et la gestion de la taille des positions minimisent les risques et améliorent les performances.

Moyenne arithmétique et moyenne géométrique

Moyenne arithmétique

Il s'agit simplement de la moyenne des rendements.
Calcul : (R1 + R2 + ... + Rn) / n.

Moyenne géométrique

Reflète le taux de croissance composé par période.
Calcul : ((1 + R1) * (1 + R2) * ... * (1 + Rn))^(1/n) - 1.
Plus précise pour évaluer les performances dans le temps en raison des effets composés.

Prenons un exemple.

Exemple de calcul

Pour le pari A et le pari B :

Pari A

50% de chances d'obtenir un rendement de +15%.
50% de chances d'obtenir un rendement de -5%.
Moyenne arithmétique : (15 + (-5)) / 2 = 5%.
Moyenne géométrique : ((1 + 0,15) * (1 - 0,05))^(1/2) - 1 ≈ 4,52%.

Pari B

50% de chances d'obtenir un rendement de +20%.
50% de chances d'obtenir un rendement de -10%.
Moyenne arithmétique : (20 + (-10)) / 2 = 5%.
Moyenne géométrique : ((1 + 0,20) * (1 - 0,10))^(1/2) - 1 ≈ 3,92%.

Impact sur les rendements à long terme

Sur plusieurs périodes, la moyenne géométrique fournit une mesure plus précise de la croissance réelle :

Effet de composition

La moyenne géométrique tient compte de la composition des rendements au fil du temps, ce qui n'est pas le cas de la moyenne arithmétique.

Impact de la volatilité

Une volatilité plus élevée fait baisser la moyenne géométrique par rapport à la moyenne arithmétique.

Cela met en évidence l'impact négatif de la variabilité sur les rendements composés.

Comparaison et impact de la volatilité

Le pari A a une moyenne géométrique plus élevée que le pari B (4,52 % contre 3,92 %), bien qu'ils aient tous deux la même moyenne arithmétique.
Au fil du temps, le pari A produira des rendements composés plus élevés en raison de sa plus faible volatilité.

Faisons cela en partant de 100 $ pour chaque pari.

Dans cet exemple, nous pouvons constater qu'après 22 périodes (chaque période de hausse et de baisse correspondant à une période), la valeur du pari A (ligne bleue) est de 279 $, tandis que celle du pari B (ligne rouge) est de 259 $.

Nous pouvons voir que la plus grande variance du pari B l'a aidé au début, puis a commencé à le distancer au fil du temps.

Explication : Une faible volatilité surpasse une forte volatilité

Traînée de la volatilité

Une volatilité plus élevée réduit davantage le rendement moyen géométrique qu'une volatilité plus faible.

C'est pourquoi les ETF à effet de levier ont tendance à être en retard sur leur facteur de levier au fil du temps.

Ils n'obtiennent leur facteur de levier que sur la période spécifiée (généralement quotidienne), et non sur plusieurs périodes, et l'effet de décalage s'aggrave avec le temps.

Cohérence

Les investissements, les transactions ou les flux de rendement à faible volatilité ont tendance à se composer plus efficacement au fil du temps, ce qui se traduit par des rendements à long terme plus élevés.

Autre exemple : - 2 % de gain/2 % de perte contre 1 % de gain/1 % de perte

Pour comparer la rapidité avec laquelle vous perdriez de l'argent avec une alternance de gains de 2 % et de pertes de 2 % par rapport à des gains de 1 % et des pertes de 1 %, nous pouvons calculer la moyenne géométrique des rendements pour chaque scénario et voir comment ils s'accumulent au fil du temps.

Scénario 1 : 2% de gain/2% de perte en alternance

Supposons que vous commenciez avec 100 $.

Après la première période : 100 $ x 1,02 = 102
Après la deuxième période : 102 $ x 0,98 = 99,96
Après la troisième période : 99,96 $ x 1,02 = 101,96
Après la quatrième période : 101,96 $ x 0,98 = 99,92 $ ... et ainsi de suite.

La moyenne géométrique du rendement pour ce scénario est : (0,98 x 1,02)^(1/2) - 1 = -0,00020

Vous serez donc perdant à long terme.

Scénario 2 : 1% de gain/1% de perte en alternance

Supposons à nouveau que vous commenciez avec 100 $.

Après la première période : 100 $ x 1,01 = 101
Après la deuxième période : 101 $ x 0,99 = 99,99
Après la troisième période : 99,99 $ x 1,01 = 100,99 $.
Après la quatrième période : 100,99 $ x 0,99 = 99,98 $ ... et ainsi de suite.

La moyenne géométrique du rendement pour ce scénario est : (0,99 x 1,01)^(1/2) - 1 = -0,00005

Ainsi, dans le scénario où l'on alterne 1% de gain et 1% de perte, vous perdrez toujours, mais seulement un quart du temps.

Cela signifie que dans le second scénario, où l'alternance des gains et des pertes est plus faible, vous perdrez de l'argent à un rythme plus lent que dans le premier scénario.

Quantification au fil du temps

Pour quantifier ce phénomène, il suffit de commencer avec 100 $ dans les deux scénarios et de les laisser se dérouler sur 100 périodes :

Dans le scénario 1 (gain/perte de 2 %), votre valeur finale sera de : $100 * (1.02 * 0.98)^50 = $98.02
Dans le scénario 2 (1% de gain/perte), votre valeur finale sera de : $100 * (1.01 * 0.99)^50 = $99.50

Ainsi, avec le scénario de gain/perte de 1 %, vous perdez de l'argent plus lentement.

Pourquoi il est très important de limiter les pertes (drawdowns)

Dans le domaine du trading, il est extrêmement important de limiter les drawdowns, car les pertes nécessitent des gains disproportionnés pour être récupérées.

Ce concept montre l'importance de la gestion de la volatilité et de la protection contre les pertes importantes.

Voici pourquoi :

L'asymétrie des pertes et des gains

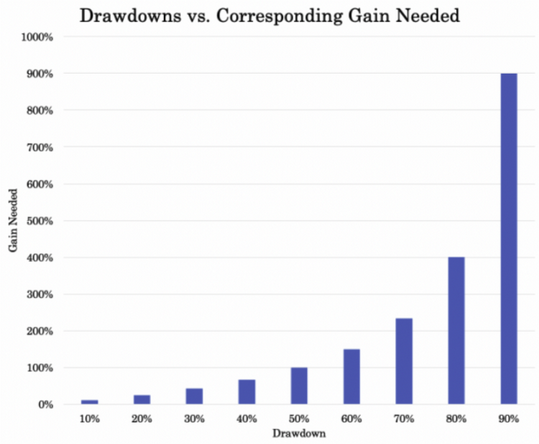
Impact mathématique des drawdowns :

Une perte de 10 % nécessite un gain de 11 % pour être récupérée.
Une perte de 20 % nécessite un gain de 25 %.
Une perte de 50 % nécessite un gain de 100 %.
Au fur et à mesure que les pertes se creusent, les gains nécessaires à la récupération augmentent de façon exponentielle.

Explication

L'accumulation des pertes :

Lorsque vous subissez une perte, votre capital de base diminue, ce qui signifie que les gains ultérieurs sont calculés sur un montant plus faible.
Par exemple, si vous commencez avec 100 $ et que vous perdez 50 %, il vous reste 50 $. Pour revenir à 100 $, vous devez doubler votre capital, ce qui représente un gain de 100 %.

Difficulté accrue de récupération :

Plus la baisse est importante, plus il est difficile et long de se rétablir.
Les petites pertes peuvent être rapidement récupérées grâce à des gains modestes, mais les pertes plus importantes nécessitent des rendements beaucoup plus élevés, qu'il est plus difficile d'obtenir de manière régulière.

Traînée de la volatilité :

Une volatilité élevée entraîne des pertes plus importantes, ce qui nuit à la performance à long terme en raison de la nature asymétrique des pertes et des gains.
Ce "frein à la volatilité" signifie que même si les rendements moyens (moyenne arithmétique) sont élevés, les rendements composés réels (moyenne géométrique) seront nettement inférieurs si l'investissement subit des pertes importantes.

Dans l'ensemble

En limitant les drawdowns, les traders peuvent protéger leur capital de manière rentable (voir ci-dessous) et s'assurer que le chemin vers la récupération des pertes est gérable.

Cette approche permet non seulement de stabiliser les rendements, mais aussi de maximiser le potentiel de croissance à long terme.

Cela souligne l'importance cruciale de gérer la volatilité et d'éviter les pertes importantes dans les stratégies de trading.

Comment procéder en pratique

Pour limiter efficacement les pertes et gérer les risques dans le cadre des opérations de trading, vous pouvez utiliser plusieurs stratégies :

1. Dimensionnement de la position

Risque par opération :

Limitez le montant du capital que vous risquez sur chaque transaction. Une règle courante consiste à ne pas risquer plus de 1 à 2 % de votre capital total sur un seul titre.
Ainsi, même une série de pertes n'entamera pas votre capital de manière significative.

Ajustez la taille de vos positions :

Ajustez la taille de votre position en fonction de la volatilité de l'actif. Pour les actifs plus volatils, optez pour des positions plus petites afin de réduire les pertes potentielles.
Des techniques telles que le critère de Kelly peuvent servir de point de départ à la théorie qui sous-tend la détermination de la taille optimale des positions.

2. La diversification

Actifs non corrélés :

Diversifiez votre portefeuille en investissant dans des actifs ou des opérations qui présentent des corrélations faibles ou négatives entre eux.
Les portefeuilles équilibrés, même dans le contexte du trading.
Cela signifie que lorsqu'un actif subit une baisse, d'autres peuvent enregistrer de bonnes performances, équilibrant ainsi la performance globale du portefeuille.

Des flux de rendement multiples :

Créez un portefeuille avec différentes stratégies ou classes d'actifs, telles que les actions, les obligations, les matières premières et les devises.
Incluez des stratégies telles que le suivi de tendance, le retour à la moyenne et l'arbitrage pour diversifier davantage les flux de rendement.

3. Utiliser les options pour réduire le risque de queue

Options de vente de protection :

Achetez des options de vente protectrices pour limiter les pertes potentielles sur vos positions.
Ces options vous donnent le droit de vendre votre actif à un prix prédéterminé, ce qui constitue un filet de sécurité si le marché évolue en votre défaveur.

Collars :

Mettez en œuvre une stratégie de collar en achetant une option de vente et en vendant une option d'achat sur le même actif.
Cette stratégie limite à la fois votre baisse et votre hausse, créant ainsi une fourchette à l'intérieur de laquelle vos rendements fluctueront.
La prime de l'option d'achat vous aide à couvrir les coûts de l'option de vente protectrice.

Stratégies d'écart :

Utilisez des stratégies de spreads comme les spreads verticaux, où vous achetez et vendez des options à des prix d'exercice différents mais avec la même date d'expiration.
Ces stratégies permettent de limiter les pertes potentielles tout en réduisant le coût d'achat des options.

4. Suivi et ajustement réguliers

Évaluation du risque :

Surveillez le profil de risque de votre portefeuille et procédez aux ajustements nécessaires.
Utilisez des outils tels que la valeur à risque (VaR) et les tests de résistance pour évaluer les pertes potentielles dans différentes conditions de marché.

Rééquilibrage :

Rééquilibrez régulièrement votre portefeuille afin de maintenir le niveau de risque souhaité.
Il s'agit d'ajuster la pondération des différents actifs pour s'assurer que votre portefeuille reste diversifié et conforme à votre tolérance au risque.

Conclusion

Comprendre la différence entre les moyennes arithmétiques et géométriques permet d'expliquer pourquoi les transactions ou les investissements à faible volatilité peuvent être plus performants que ceux à forte volatilité sur le long terme.

La moyenne géométrique, qui tient compte des effets de composition, donne une image plus claire de la performance réelle des investissements.

En dimensionnant soigneusement les positions, en diversifiant les actifs, les transactions et les flux de rendement non corrélés, en utilisant des options pour gérer le risque d'écart, en surveillant et en ajustant régulièrement votre portefeuille, vous pouvez limiter efficacement les baisses et protéger votre capital.

Ces stratégies permettent de stabiliser les rendements et d'améliorer le potentiel de croissance à long terme.

#1 26-05-2024 14:28:52