#1 01-01-2024 16:40:19

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 092

Le critère de Kelly

Le critère de Kelly est une formule mathématique utilisée pour déterminer la taille optimale d'une série de paris.

Développé par John L. Kelly Jr. en 1956, il a trouvé des applications dans les jeux de hasard, le trading, l'investissement et la gestion des risques.

Le critère vise à maximiser le logarithme de la richesse.

Cela offre un avantage stratégique dans les scénarios où les probabilités de résultats sont connues.

Fondation mathématique

Le critère de Kelly calcule la proportion d'un portefeuille à miser, en fonction du rendement attendu et des cotes du pari.

La formule s'exprime ainsi :

Pourcentage de Kelly = pb – q/b

Où:

• p est la probabilité d'un pari gagnant,

• q est la probabilité de perdre (q = 1 − p),

• b est la cote reçue sur le pari (et non la probabilité), définie comme les gains potentiels divisés par le montant misé.

Exemple du critère de Kelly

Supposons que vous ayez un pari où :

• La probabilité de gagner (p) est de 0,55 (soit 55 %).

• La probabilité de perdre (q) est de 0,45 (soit 45 %).

• La cote reçue sur le pari (b) est de 1 (pair).

Selon le critère de Kelly, si vous avez un avantage avec 55 % de chances de gagner et des cotes égales, vous devez miser 10 % de votre bankroll sur chaque pari afin de maximiser le taux de croissance de votre richesse.

Cette approche vise à équilibrer les objectifs de maximisation des rendements tout en minimisant le risque de perdre la totalité de la bankroll.

Cela peut permettre une croissance soutenue sur de nombreux paris.

Simulation de l'accumulation de richesse à l'aide du critère de Kelly

Allons plus loin que ce que nous avons décrit ci-dessus et exécutons une simulation de 520 paris (10 ans d'un pari par semaine) où vous obtenez une probabilité de 55/45 (en votre faveur) sur chaque pari et une cote de 1 : 1.

Le graphique ci-dessous illustre la trajectoire de l'accumulation de richesse au fil du temps en utilisant le critère de Kelly dans ce scénario de pari.

Ici, la richesse initiale est fixée à 100 unités, et l'individu effectue une série de paris au fil du temps.

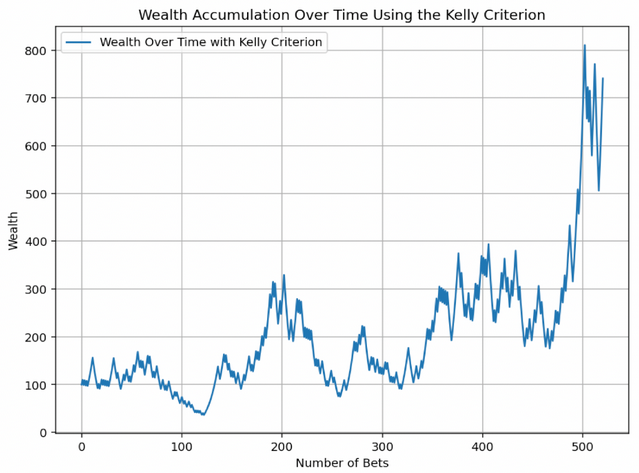
Le bon côté du critère de Kelly

Comme le montre le graphique, la richesse a tendance à augmenter avec le temps.

Cela démontre l'effet cumulatif du réinvestissement des gains selon le critère de Kelly.

Cette simulation montre comment l'utilisation du critère de Kelly peut conduire à une croissance de la richesse dans un contexte probabiliste avec un avantage positif.

Le mauvais côté du critère de Kelly

Mais cela montre aussi l'autre côté du critère de Kelly.

Les drawdowns à partir de la ligne des hautes eaux seront brutales.

On peut voir qu'entre les mises 200 et 250, le trader/joueur a perdu environ 70% de son argent.

Il a ensuite rapidement doublé à nouveau avant de perdre rapidement ce qu'il avait gagné.

Il enchaîne ensuite une grosse séquence de mises entre 460 et 500, quadruplant ainsi son argent.

Lorsqu'il atteint 800, il perd ensuite rapidement plus de 35 %, avant de remonter à nouveau.

C'est un bon retour sur investissement.

Mais le critère de Kelly crée beaucoup de volatilité qui le place davantage à la portée d'un joueur en quête de risque que d'un trader recherchant des gains relativement réguliers au fil du temps.

Beaucoup auraient psychologiquement du mal à gérer ce niveau de volatilité et ce type de gestion de bankroll.

Plus de simulations du critère de Kelly

Pour nous amuser, nous avons effectué deux autres simulations.

Celui ci-dessous est une grande chance, transformant 100 en plus de 25 000 sur 520 paris en utilisant le critère de Kelly.

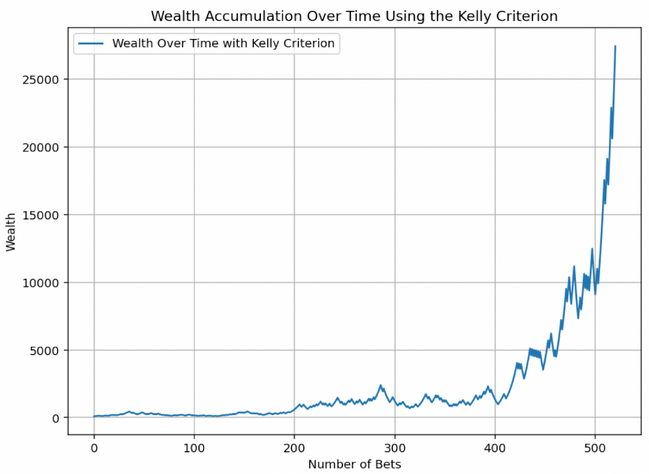
Celui-ci a de la chance tôt – et plus vite – mais hésite au fil du temps.

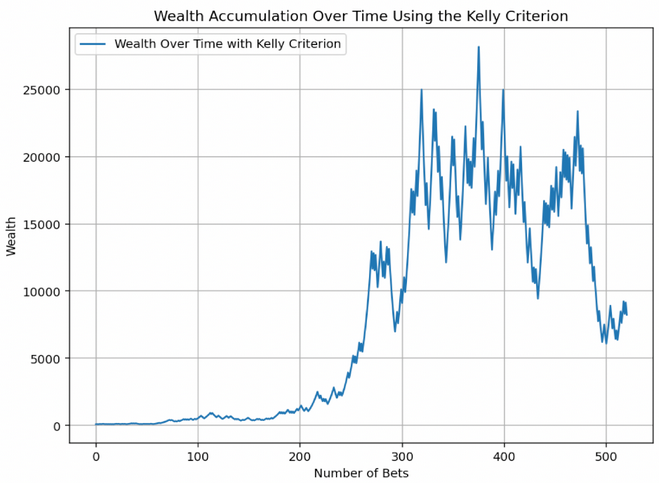
Code source

Si vous souhaitez essayer cela par vous-même, voici le code Python :

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the simulation
np.random.seed(42) # for reproducible results
initial_wealth = 100 # initial wealth
n_bets = 520 # number of bets (e.g., 10 years of weekly bets)
b = 1 # odds (b to 1)
p = 0.55 # probability of winning each bet
fraction_kelly = 1 # Fraction of the Kelly Criterion to bet; 1 for full Kelly

# Calculate the Kelly fraction
kelly_fraction = (b * p - (1 - p)) / b

# Simulate the wealth over time using the Kelly Criterion
wealth = [initial_wealth]
for _ in range(n_bets):
bet_size = fraction_kelly * kelly_fraction * wealth[-1]
win = np.random.rand() < p # win or lose the bet
if win:
wealth.append(wealth[-1] + bet_size * b) # update wealth if win
else:
wealth.append(wealth[-1] - bet_size) # update wealth if lose

# Plotting the results
plt.figure(figsize=(12, 6))
plt.plot(wealth, label="Wealth Over Time with Kelly Criterion")
plt.title("Wealth Accumulation Over Time Using the Kelly Criterion")
plt.xlabel("Number of Bets")
plt.ylabel("Wealth")
plt.legend()
plt.grid(True)
plt.show()

Si vous utilisez ce code, assurez-vous de mettre en retrait le cas échéant :

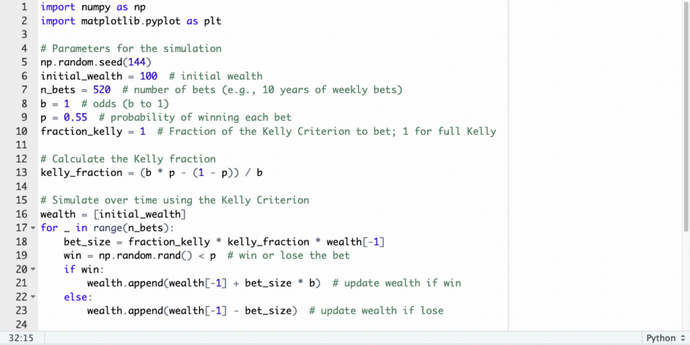
Valeur attendue du critère de Kelly

Lançons une simulation pour comprendre la valeur attendue de cette expérience au milieu des niveaux de variance extrêmes induits par le critère de Kelly.

• p = 0,55 (probabilité de gagner)

• q = 1 − p = 0,45 (probabilité de perdre)

• b = 1 (le pari rapporte b à 1 ; ici, c'est pair, donc b = 1)

p = 0.55 # probability of winning
q = 1 - p # probability of losing
b = 1 # even money odds
n_bets = 520 # number of bets
initial_wealth = 100 # starting wealth

# Kelly fraction
kelly_fraction = (p - q) / b

# Expected log growth rate per bet using Kelly Criterion
expected_log_growth_per_bet = p * np.log(1 + kelly_fraction * b) + q * np.log(1 - kelly_fraction)

# Expected log growth over 520 bets
total_expected_log_growth = n_bets * expected_log_growth_per_bet

# Expected wealth after 520 bets
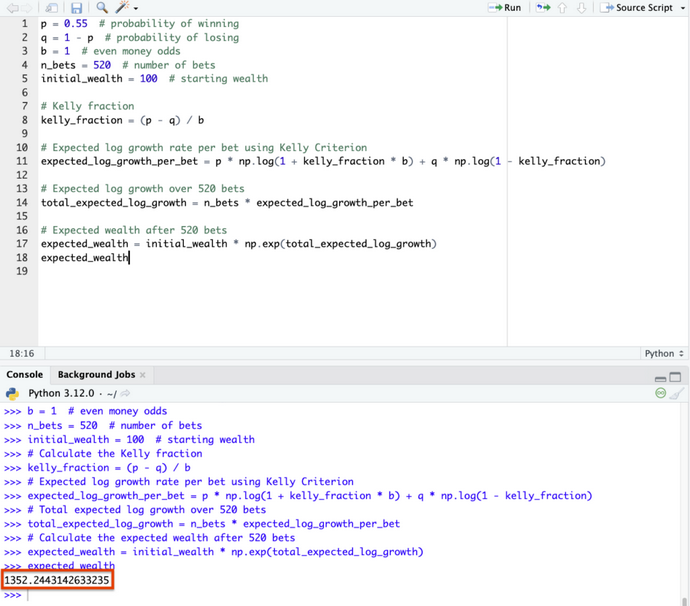
expected_wealth = initial_wealth * np.exp(total_expected_log_growth)
expected_wealth

Et nous avons une valeur attendue de 1 352 (13,5x le retour sur investissement après 520 paris), ce qui montre que nous n'avons pas eu de chance dans la première simulation et que nous avons eu de la chance dans la deuxième et la troisième.

Application en finance

En finance, le critère de Kelly est utilisé pour réfléchir à la taille des positions et aux risques du portefeuille.

Cela peut servir de facteur déterminant pour déterminer le montant de capital à allouer à chaque transaction.

En prenant en compte la probabilité de rendements positifs et les résultats des transactions réussies, il peut orienter la taille des transactions afin de maximiser le taux de croissance du capital au fil du temps.

Néanmoins, le critère de Kelly n'est pas le plus approprié dans le contexte d'un portefeuille sophistiqué où la corrélation, la covariance et divers autres facteurs entrent en jeu.

Mais l'idée générale de parier davantage sur quelque chose lorsque les chances sont plus en votre faveur et que vous obtenez de bons gains ou des primes de risque reste vraie – même dans le contexte de ceux qui souhaitent détenir des portefeuilles équilibrés.

Avantages

Croissance du capital à long terme

Le critère de Kelly vise à maximiser la croissance du capital à long terme.

Il équilibre le compromis entre risque et récompense.

Gestion des risques

Il prend intrinsèquement en compte le risque de ruine et ajuste le montant de la mise en conséquence.

Il agit comme une mesure de protection contre des pertes importantes.

Intérêts composés

Puisque la stratégie est axée sur le logarithme de la richesse, elle profite implicitement de la composition, un aspect clé de l'accumulation de richesse.

Limites

Exigence de probabilités précises

La plus grande limite réside dans la nécessité de disposer de probabilités précises de résultats, qui peuvent être difficiles à estimer dans des scénarios réels.

Dans le monde réel, vous savez rarement quelles sont vos chances.

Performance volatile à court terme

Cette approche peut conduire à une forte volatilité à court terme, car elle suggère souvent un dimensionnement agressif.

Par exemple, dans notre exemple ci-dessus, un pari 55/45 avec des cotes paires suggère une mise de 10 %.

C'est assez élevé et cela entraînerait beaucoup de variations.

Sensibilité aux erreurs d'estimation

La formule est sensible aux erreurs de probabilité et d'estimation des gains, ce qui peut conduire à des tailles de paris sous-optimales.

Statique

Les probabilités et les gains sur les marchés fluctuent généralement (et, encore une fois, sont difficiles à estimer).

Considérations pratiques

Paris fractionnés sur Kelly

Pour atténuer les risques, les traders utilisent souvent une fraction du critère de Kelly (par exemple, la moitié du Kelly).

Cela réduit les rendements potentiels mais diminue également le risque et la volatilité.

Application diversifiée

Au-delà de la finance, le critère est utilisé dans les paris sportifs, les jeux de hasard et d'autres domaines où se produisent des résultats probabilistes avec des cotes connues.

Intégration avec d'autres stratégies

Il est souvent utilisé en conjonction avec d'autres stratégies de gestion des risques et de trading/investissement pour une approche plus équilibrée.

Conclusion

Le critère de Kelly est utilisé pour la prise de décision dans des environnements probabilistes.

Sa capacité à maximiser la richesse sur le long terme, tout en tenant compte du risque de pertes importantes, en fait au moins quelque chose à comprendre pour les traders.

Néanmoins, son efficacité dépend de l'estimation précise des probabilités et des gains.

C'est un défi dans de nombreux scénarios pratiques.

Courtiers pour investir en bourse

Investir comporte des risques de perte

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.