Vous n'êtes pas identifié(e).
- Contributions: Récentes | Sans réponse
#1 13-02-2024 19:20:18
- Climax
- Administrateur

- Inscription: 30-08-2008
- Messages: 6 411


La géométrie complexe dans la finance, les marchés et le trading

La géométrie complexe - en particulier la géométrie fractale et d'autres concepts mathématiques avancés - a des applications uniques dans les domaines de la finance, des marchés et du trading.
Ces applications permettent de modéliser les modèles et les structures des données financières d'une manière qui n'est normalement pas possible (c'est-à-dire en intégrant l'utilisation de nombres complexes) afin de comprendre les comportements du marché, de prédire les tendances et de gérer les risques de manière plus efficace.
Points clés :
➡️ La géométrie complexe est l'étude des formes, des espaces et des dimensions qui sont régis par des nombres complexes, ce qui permet d'explorer des structures et des relations plus complexes que celles que l'on trouve dans la géométrie traditionnelle. Par exemple, elle permet de représenter des données où une variable d'entrée inconnue élevée à une puissance paire donne un nombre négatif (par exemple, x^2 = -1), ce qui n'est pas possible avec les nombres/la géométrie standard.
➡️ Modélisation de la dynamique du marché - La géométrie complexe permet de saisir de manière unique les relations et les modèles au sein des modèles, ce qui permet d'obtenir des prédictions et des évaluations des risques plus précises.
➡️ Optimisation des portefeuilles - En comprenant la structure géométrique des portefeuilles (ou des données financières, plus généralement), les traders peuvent optimiser l'allocation des actifs afin d'améliorer les rendements tout en gérant les risques. La courbure de l'espace est utilisée pour identifier les trajectoires d'allocation optimales (ou tout ce qui est modélisé).
➡️ Naviguer dans les risques - La géométrie complexe permet de visualiser et de gérer la nature multidimensionnelle des risques financiers, de la volatilité du marché à l'exposition au crédit. La géométrie complexe permet de visualiser et de gérer la nature multidimensionnelle des risques financiers, de la volatilité des marchés à l'exposition au risque de crédit.
Voici quelques concepts clés et applications de la géométrie complexe dans ces domaines :
1. La géométrie fractale dans l'analyse des marchés
Les fractales sont des motifs autosimilaires qui se répètent à différentes échelles.
Sur les marchés financiers, les mouvements de prix présentent souvent un comportement fractal.
Cela suggère que les modèles dans les données de prix peuvent se répéter dans le temps et à différentes échelles.
Application
Les traders utilisent la géométrie fractale pour identifier les schémas répétitifs dans les graphiques de prix, qui peuvent indiquer des points potentiels de renversement ou de poursuite de la tendance.
La théorie de la vague d'Elliott en est un exemple, qui propose que les marchés évoluent selon des vagues prévisibles de nature fractale.
2. Réseaux complexes dans les systèmes financiers
Les marchés financiers peuvent être modélisés comme des réseaux complexes, où :
les nœuds représentent des entités (telles que des actions, des secteurs ou des pays), et
les arêtes représentent les connexions ou les corrélations entre ces entités.
Application
L'analyse de la structure de ces réseaux permet de comprendre les risques systémiques, les effets de contagion et la résilience des systèmes financiers.
Par exemple, un réseau étendu et densément interconnecté peut être plus sensible aux défaillances systémiques.
3. Théorie du chaos et dynamique non linéaire
Les marchés financiers sont des systèmes dynamiques qui peuvent présenter un comportement "chaotique" - sensible aux conditions initiales et caractérisé par une dynamique non linéaire.
Cela signifie que de petits changements peuvent conduire à des résultats très différents et qu'il existe de nombreuses dépendances.
Il est donc difficile de prévoir les mouvements du marché sur de longues périodes - c'est-à-dire que vos distributions s'élargissent avec le temps.
Application
Les traders et les analystes utilisent la théorie du chaos pour comprendre la volatilité des marchés et élaborer des stratégies commerciales.
Cette théorie souligne l'importance de penser de manière probabiliste et d'utiliser des techniques de gestion du risque pour faire face à la grande quantité d'inconnues par rapport à la quantité de connaissances par rapport à ce qui est escompté dans le prix.
4. Analyse de données à haute dimension
Les données financières sont souvent hautement dimensionnelles, de nombreuses variables influençant les mouvements du marché.
Les techniques issues de la géométrie complexe, telles que l'apprentissage multiple et l'analyse topologique des données, permettent de découvrir des structures dans cet espace à haute dimension.
Application
Ces techniques sont utilisées pour la réduction de la dimensionnalité, le regroupement et la visualisation des données financières.
Elles permettent d'identifier des modèles, des corrélations et des anomalies qui ne sont pas apparents dans les analyses traditionnelles.
5. Modèles d'évaluation des options
Les modèles avancés d'évaluation des options et autres produits dérivés impliquent souvent la résolution d'équations aux dérivées partielles qui décrivent l'évolution des prix dans le temps.
Ces équations peuvent avoir des solutions de nature géométrique et impliquer des formes et des surfaces complexes dans des espaces à haute dimension.
Application
Le modèle de Black-Scholes et ses extensions utilisent ces concepts pour fournir des prix théoriques pour les options en tenant compte de facteurs tels que la volatilité, la décroissance temporelle et les mouvements de prix de l'actif sous-jacent.
6. Optimisation de portefeuille
Le problème de l'optimisation d'un portefeuille afin d'obtenir le meilleur rendement possible pour un niveau de risque donné peut être formulé de manière géométrique, les solutions se situant sur la frontière efficiente dans l'espace risque-rendement.
Il s'agit d'un exemple de collecteur 3D, montrant le rendement attendu et la volatilité sur les axes x et y et le ratio de Sharpe sur l'axe z.

L'exemple suivant est un manifold statistique en 3D, où le fait d'atteindre un point plus élevé et plus plat sur le graphique permet une meilleure optimisation du portefeuille.
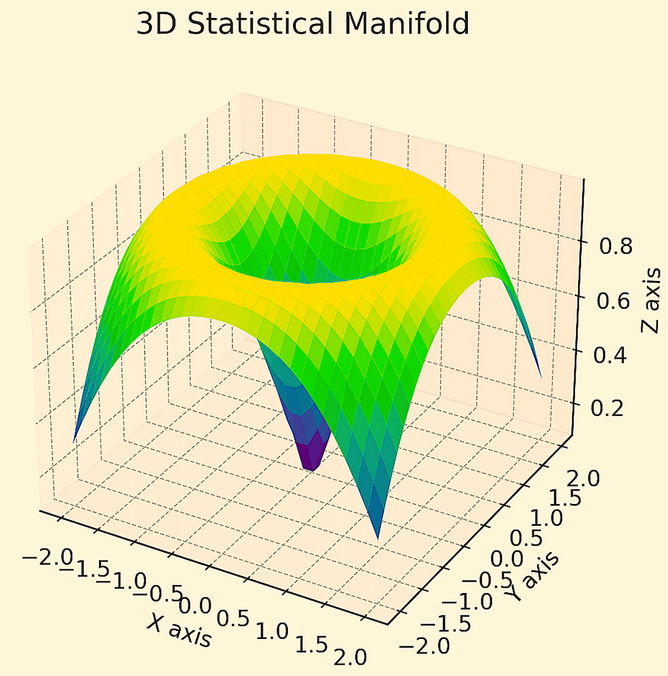
Application
Les techniques de la géométrie complexe sont appliquées pour explorer cet espace afin d'identifier les répartitions optimales du portefeuille.
Il s'agit d'équilibrer le portefeuille entre différents actifs afin de minimiser le risque tout en visant des profils de rendement spécifiques.
Géométrie complexe et apprentissage automatique dans la finance et le trading
La géométrie complexe permet de modéliser les structures complexes des données financières et la dynamique des marchés, ce qui aide à comprendre la diversification des portefeuilles et la gestion des risques.
De leur côté, les algorithmes d'apprentissage automatique tirent des enseignements de vastes ensembles de données pour découvrir des modèles cachés, optimiser les stratégies de trading et améliorer la prise de décision.
Ensemble, ils permettent aux traders et aux analystes d'améliorer l'allocation des actifs et de minimiser les risques grâce à une modélisation flexible et à des cadres mathématiques.
Exemple de codage - La géométrie complexe dans le trading
Un exemple d'application de la géométrie complexe au trading serait l'optimisation d'un portefeuille où nous avons une variable d'entrée élevée à une puissance paire et la solution étant un nombre négatif (par exemple, la vente à découvert, où l'allocation vers quelque chose est négative).
Nous pouvons modéliser le concept à l'aide de Python en nous concentrant sur un scénario simplifié d'optimisation de portefeuille avec des contraintes permettant la vente à découvert.
Nous utiliserons Python pour optimiser un portefeuille à deux actifs et intégrerons des concepts de géométrie complexe en considérant la possibilité que les rendements des actifs soient des nombres complexes, afin de démontrer le traitement des valeurs négatives - par exemple, la vente à découvert dans le contexte de certaines procédures d'optimisation de portefeuille.
Exemple de code Python
Cet exemple ne visualisera pas directement des manifolds géométriques complexes, mais montrera comment configurer un problème d'optimisation qui inclut la possibilité de vente à découvert, modélisé par le programme Python scipy.optimize pour l'optimisation numérique :
import numpy as np
from scipy.optimize import minimize
# Exemple de rendement pour deux actifs (pourrait être étendu pour inclure des scénarios complexes)
# Ici, nous utilisons simplement des nombres réels pour la démonstration
returns = np.array([0.1, 0.2]) # Expected returns for asset 1 & asset 2
# Matrice de covariance des actifs
cov_matrix = np.array([[0.005, -0.002],
[-0.002, 0.004]])
# Fonction objective de maximisation (négative pour la fonction de minimisation) du rendement attendu
# Ajout de complexité en autorisant la vente à découvert, où l'allocation peut être négative
def objective(weights):
return -np.dot(weights, returns)
# Contraintes : somme des poids = 1
constraints = ({'type': 'eq', 'fun': lambda weights: np.sum(weights) - 1})
# Les limites de chaque poids permettent la vente à découvert (pas de limite)
bounds = ((-np.inf, np.inf), (-np.inf, np.inf))
# Estimation initiale (répartition égale)
init_guess = [0.5, 0.5]
# Optimisation du portefeuille
opt_results = minimize(objective, init_guess, method='SLSQP', bounds=bounds, constraints=constraints)
print("Optimal Weights:", opt_results.x)
print("Expected Portfolio Return:", -opt_results.fun)Explication
Fonction objective - Définie pour maximiser le rendement attendu ; elle est négative ici parce que la fonction de minimisation recherche la valeur la plus basse.
Contraintes et limites - Veiller à ce que la somme des poids soit égale à 1 (maintien de l'investissement total) et autoriser des poids négatifs, représentant la vente à découvert.
Optimisation - Utilise scipy.optimize.minimize avec la méthode SLSQP (Sequential Least SQuares Programming), adaptée aux problèmes d'optimisation avec contraintes.
Ce code fournit une approche fondamentale de l'optimisation de portefeuille, y compris des éléments tels que la vente à découvert, en utilisant Python.
Bien qu'il ne modélise pas explicitement le manifold ou n'implique pas directement les nombres complexes, le concept d'autoriser des poids négatifs laisse entrevoir l'inclusion de stratégies de nombres complexes (comme la vente à découvert) dans l'optimisation de portefeuille.
Conclusion
L'application de la géométrie complexe à la finance, aux marchés et au trading offre un moyen unique d'analyse, de prédiction et de gestion des risques.
En explorant de nouvelles façons d'analyser la complexité et les modèles des données financières, les traders, les investisseurs et les analystes peuvent obtenir des informations plus approfondies sur les données du marché et améliorer leurs processus de prise de décision.
En rapport :
Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.
Hors ligne
- Utilisateurs enregistrés en ligne dans ce sujet: 0, invités: 1
- [Bot] ClaudeBot
