#1 19-06-2024 21:14:37

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 362

Trading de moments (probabilités) statistiques

Le trading de moments statistiques est une stratégie de trading quantitative qui s'appuie sur le concept mathématique des moments pour analyser et prédire le comportement du marché.

Elle implique l'utilisation de divers moments statistiques pour comprendre la distribution et les caractéristiques des prix des actifs, ce qui aide les traders à prendre de meilleures décisions.

L'optimisation de la moyenne-variance est une approche classique de la finance, mais des approches plus modernes comprennent la forme et les caractéristiques plus profondes des distributions - c'est-à-dire l'asymétrie et la queue de la distribution plutôt que, par exemple, de considérer la volatilité comme un écart-type de base.

Les événements de queue peuvent modifier considérablement les performances à long terme des stratégies de trading, d'où l'importance de comprendre les distributions de probabilités et leurs moments.

Points clés :

Saisir le retour à la moyenne

• Le moment trading statistique se concentre sur des concepts tels que le retour à la moyenne (qui permet aux traders de profiter des écarts de prix qui reviennent à la moyenne).

Mesures statistiques

• Les traders utilisent des moments tels que la moyenne, la variance, l'asymétrie et l'aplatissement pour identifier les opportunités de trading et comprendre leurs distributions.

Gestion du risque

• En comprenant les moments statistiques, les traders peuvent mieux optimiser leurs portefeuilles.

Aperçu des moments statistiques

Les moments statistiques sont des mesures quantitatives utilisées pour décrire la forme et les caractéristiques d'une distribution de probabilité.

Les moments les plus couramment utilisés en trading sont les quatre premiers :

• Moyenne

• Variance

• Asymétrie (skewness)

• Aplatissement (kurtosis)

Pour une distribution normale, l'asymétrie et l'aplatissement sont nuls. C'est la seule forme de distribution pour laquelle cela est vrai.

Toutefois, les distributions de rendements financiers présentent généralement une asymétrie et des queues grasses (aplatissement), comme dans le cas suivant :

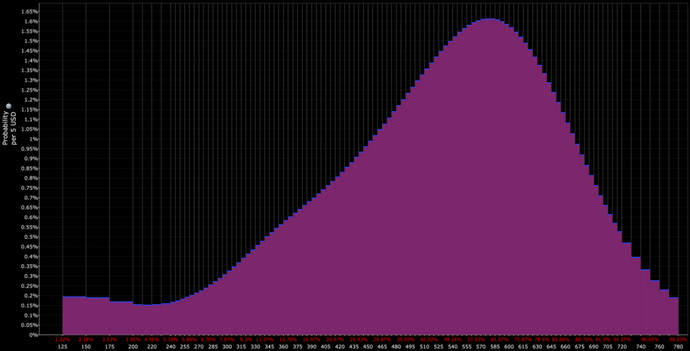
Moyenne (premier moment)

La moyenne est la valeur moyenne de tous les points de données d'une distribution.

Dans le domaine du trading, elle représente le rendement attendu d'un actif.

En analysant la moyenne, les traders peuvent identifier la tendance centrale des mouvements de prix et faire des prévisions sur les niveaux de prix futurs.

Variance (deuxième moment)

La variance mesure la dispersion des points de données autour de la moyenne.

Dans le contexte du trading, la variance indique la volatilité d'un actif.

Une variance élevée indique un risque plus important, car les prix sont plus dispersés, tandis qu'une variance faible indique des prix plus stables.

Asymétrie (troisième moment)

Le skewness mesure l'asymétrie de la distribution.

Une asymétrie positive indique que la distribution a une longue queue droite, ce qui suggère que les petites pertes sont fréquentes et les gains importants occasionnels.

Une asymétrie négative, en revanche, indique une longue queue gauche, ce qui laisse supposer des gains faibles fréquents et des pertes importantes occasionnelles.

Comprendre l'asymétrie aide les traders à anticiper la direction et l'ampleur des mouvements de prix potentiels.

Aplatissement (quatrième moment)

Le kurtosis mesure la "queue" de la distribution.

Un kurtosis élevé signifie que la distribution a des queues lourdes et des pics aigus, ce qui indique une probabilité plus élevée de mouvements de prix extrêmes.

Un kurtosis faible indique des queues plus légères et un pic plus plat, ce qui suggère moins de mouvements de prix extrêmes.

Les traders utilisent le kurtosis pour évaluer le risque d'événements extrêmes sur le marché.

Moments d'ordre supérieur au-delà du kurtosis

Les moments d'ordre supérieur, au-delà du quatrième moment, fournissent des informations plus approfondies sur la forme et le comportement d'une distribution. Ils sont souvent utilisés dans des analyses statistiques et financières plus avancées :

Cinquième moment

Mesure l'asymétrie et le comportement de la queue.

Étend l'asymétrie en capturant des écarts plus nuancés par rapport à la symétrie.

Sixième moment

Capture l'étendue et l'impact des valeurs extrêmes, élargit le kurtosis en identifiant des valeurs aberrantes plus extrêmes.

Septième et huitième moments

Rarement utilisés, ils peuvent fournir des détails supplémentaires sur la forme de la distribution, en se concentrant sur des aspects plus complexes de l'asymétrie et du comportement de la queue.

Ces moments d'ordre supérieur sont moins couramment utilisés en raison de leur complexité et de leur utilité pratique décroissante dans de nombreuses applications du monde réel.

Ils peuvent toutefois être utilisés dans des domaines nécessitant une évaluation précise des risques et une modélisation des événements extrêmes, comme dans certains secteurs de la finance et de l'assurance.

Application au trading

Le trading de moments statistiques applique ces moments pour créer des modèles qui prédisent les mouvements de prix et la volatilité futurs.

Voici comment chaque moment est utilisé :

Retour à la moyenne

Les traders qui utilisent des stratégies de retour à la moyenne partent du principe que les prix des actifs reviendront à leur moyenne historique au fil du temps.

En identifiant les écarts par rapport à la moyenne, ils peuvent acheter des actifs sous-évalués et vendre des actifs surévalués, en s'attendant à ce que les prix reviennent vers la moyenne.

Prévision de la volatilité

La variance est utilisée pour prévoir la volatilité.

Les traders analysent la variance historique pour prédire les fluctuations futures des prix et adapter leurs stratégies de trading en conséquence, et comprendre les changements structurels qui ont eu lieu et qui font que la volatilité future est susceptible de différer de la volatilité historique.

Par exemple, dans des environnements à forte volatilité, les traders peuvent réduire la taille de leurs positions pour gérer le risque.

(Les teneurs de marché élargissent généralement les écarts entre les cours acheteur et vendeur).

Analyse de l'asymétrie

L'analyse de l'asymétrie permet aux traders de prédire la direction des mouvements de prix futurs.

• Une asymétrie positive indique une distribution dont la queue est asymétrique et s'étend vers des valeurs plus positives.

• Une asymétrie négative indique une distribution avec une queue asymétrique allant vers des valeurs plus négatives.

Gestion du risque de queue

Le coefficient d'aplatissement est utilisé pour évaluer le risque d'événements extrêmes sur le marché.

Un kurtosis élevé suggère une probabilité plus élevée de variations importantes des prix, ce qui incite les traders à mettre en œuvre des stratégies de gestion des risques telles que des ordres stop-loss ou des opérations de couverture (par exemple, des options de vente) afin de protéger leurs portefeuilles.

Techniques de mise en œuvre

Le trading de moments statistiques nécessite des systèmes et des techniques informatiques pour analyser de grands ensembles de données et calculer les moments.

Les méthodes les plus courantes sont les suivantes :

Logiciels statistiques

Les traders utilisent souvent des logiciels statistiques tels que R, Python et MATLAB pour calculer les moments et effectuer l'analyse des données.

Ces outils offrent des bibliothèques et des fonctions puissantes pour la modélisation et la visualisation statistiques.

Apprentissage automatique

Les algorithmes d'apprentissage automatique peuvent améliorer l'analyse des moments statistiques en identifiant des modèles et des relations qui ne sont pas apparents dans les méthodes traditionnelles.

Des techniques telles que l'analyse de régression, le clustering et les réseaux neuronaux peuvent être appliquées pour améliorer la précision des prédictions.

Données en temps réel

Les plateformes de trading à haute fréquence et les API fournissent les flux de données nécessaires.

Avantages et limites

👍 Avantages

• Précision - Les moments statistiques fournissent des mesures quantitatives précises permettant d'améliorer la précision des modèles de trading.

• Gestion du risque - La compréhension des caractéristiques de distribution des prix des actifs permet aux traders de mieux gérer le risque et d'éviter les pertes extrêmes.

• Polyvalence - L'approche peut être appliquée à différentes classes d'actifs, notamment les actions, les matières premières et les devises.

• Logiciel - De nombreux logiciels (par exemple, Python) sont capables de calculer les quatre premiers moments/cumulants (moyenne, variance, skew, kurtosis) des données.

👎 Limites

• Complexité - Les besoins mathématiques et informatiques du trading des moments statistiques requièrent des compétences et des ressources.

• Dépendance à l'égard des données - La précision des calculs des moments dépend de la qualité et de l'exhaustivité des données historiques.

• Hypothèses de marché - L'hypothèse selon laquelle les moments historiques permettent de prédire le comportement futur n'est pas toujours valable, en particulier lorsque l'avenir est différent du passé.

---

Examinons quelques transactions impliquant le trading de moments statistiques :

Exemple 1 : Stratégie de retour à la moyenne

➡️ Choisissez une action, par exemple XYZ Corp, qui se négocie actuellement à 100 $ l'action.

➡️ Analysez les données historiques du cours de la société XYZ pour déterminer le cours moyen historique. Supposons que le prix moyen historique soit de 95 $.

➡️ Identifiez l'écart actuel par rapport à la moyenne. Dans ce cas, l'action se négocie à 100 $, soit 5 $ de plus que la moyenne historique.

➡️ Détermination du point d'entrée : Fixez un seuil d'écart qui signale une opération de retour à la moyenne. Supposons que ce seuil soit de 4 $. Comme le cours actuel est supérieur de 5 $ à la moyenne, il dépasse le seuil.

➡️ Vendez à découvert 100 actions de la société XYZ à 100 $ l'action, en prévoyant que le cours reviendra à la moyenne.

➡️ Surveillez l'évolution du cours.

➡️ Lorsque le cours revient à la moyenne de 95 $, couvrir la position courte en achetant 100 actions à 95 $ l'action.

Détails de l'opération

• Prix d'entrée : 100 $ par action

• Actions vendues à découvert : 100

• Prix de sortie : 95 $ par action

• Profit : (100 - 95) * 100 = 500 $

Exemple 2 : Prévision de la volatilité

➡️ Choisissez un actif. Appelons-le ABC Futures.

➡️ Calculez la variance historique des prix des contrats à terme ABC sur une période donnée. Supposons que la variance soit de 0,04 (4 %).

➡️ Utilisez la variance historique pour prévoir la volatilité future. Supposons que la variance prévue pour le mois suivant soit de 0,05 (5 %).

➡️ Ajustez la taille de la position en fonction de la volatilité prévue. Si la taille habituelle de la position est de 10 contrats, réduisez-la de 20 % en raison de l'augmentation de la volatilité prévue.

➡️ Achetez 8 contrats à terme ABC au lieu de 10 pour gérer le risque associé à une volatilité plus élevée.

➡️ Placez des ordres stop-loss ou des options pour vous protéger contre les mouvements de prix défavorables. Par exemple, fixer un stop-loss à 2 % en dessous du prix d'entrée.

Détails de l'opération

• Taille de la position standard : 10 contrats

• Taille de position ajustée : 8 contrats

• Prix d'entrée : Supposons que le prix d'entrée soit de 1 000 $ par contrat

• Niveau de stop-loss : 980 $ par contrat (2 % en dessous du prix d'entrée)

Exemple 3 : Analyse de l'asymétrie

L'asymétrie est une mesure de l'asymétrie de la distribution de probabilité des rendements pour un investissement donné.

Interprétation de l'asymétrie

• Asymétrie positive - Indique un potentiel de rendements positifs extrêmes, mais moins fréquents. Un trader peut y voir une opportunité de hausse importante.

• Asymétrie négative - Indique un potentiel de rendements extrêmement négatifs, suggérant un risque de pertes importantes. Un trader peut agir avec prudence ou couvrir ses positions.

Développement de la stratégie

• Asymétrie positive - Les traders peuvent opter pour des stratégies qui capitalisent sur la probabilité d'événements positifs, comme l'achat d'options d'achat hors de la monnaie.

• Asymétrie négative - Les traders peuvent mettre en œuvre des stratégies de gestion des risques telles que des ordres stop-loss ou l'achat d'options de vente pour se protéger contre les mouvements négatifs extrêmes.

Exemple pratique

• Supposons qu'un trader analyse une action et trouve une asymétrie de 0,8 (asymétrie positive). Il peut décider de prendre une position longue, en anticipant que l'action/l'actif a une probabilité plus élevée d'obtenir des rendements positifs.

• À l'inverse, si l'asymétrie est de -0,5 (asymétrie négative), il peut choisir d'éviter de prendre une position longue ou d'utiliser des options de vente/options de protection pour se prémunir contre d'éventuelles pertes importantes.

Exemple 4 : Gestion du risque de queue (Kurtosis)

➡️ Choisissez un actif.

➡️ Trouvez l'aplatissement attendu de la distribution des prix de l'actif. Supposez que l'aplatissement est élevé, ce qui indique la probabilité de mouvements de prix extrêmes.

➡️ Mettre en œuvre une stratégie de couverture contre les mouvements de prix extrêmes potentiels. Acheter des options de vente hors de la monnaie (OTM) à titre d'assurance.

➡️ Choisissez des options de vente OTM dont le prix d'exercice est inférieur de 10 % au prix actuel. Supposons que le cours actuel est de 200 dollars par action. Achetez donc des options de vente avec un prix d'exercice de 180 dollars.

➡️ Achetez 10 contrats d'options de vente (chaque contrat représente généralement 100 actions) avec un prix d'exercice de 180 $.

➡️ Ajustez si nécessaire en fonction des mouvements de prix et des changements dans l'aplatissement (kurtosis).

Détails de l'opération

• Prix actuel : 200 $ par action

• Prix d'exercice des options de vente : 180 $

• Nombre de contrats : 10

• Coût par contrat d'option : 2 $ par action (coût total = 10 * 100 * 2 $ = 2 000 $)

Conclusion

Le trading de moments statistiques est une stratégie qui exploite les propriétés mathématiques des distributions pour améliorer les décisions d'investissement.

En comprenant et en appliquant les concepts de moyenne, de variance, d'asymétrie et d'aplatissement (et éventuellement des moments d'ordre supérieur), les traders peuvent mieux comprendre la nature de leurs rendements attendus et apprendre à optimiser leurs portefeuilles - ou au moins être conscients de certains risques.

Brokers d'options

Investir comporte des risques de perte

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.