#1 04-02-2024 17:17:27

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 362

Modèles de treillis dans la finance et le trading

Les modèles de treillis sont largement utilisés dans l'évaluation des produits financiers dérivés, la gestion des risques et l'élaboration de stratégies de négociation et d'investissement.

Ils fournissent un cadre structuré et discret pour modéliser l'évolution des variables financières dans le temps.

Ils sont donc particulièrement utiles dans les scénarios où les modèles continus sont soit trop complexes, soit inappropriés.

Principaux enseignements

Flexibilité dans la fixation du prix

• Les modèles de treillis, comme les arbres binomiaux, permettent de fixer le prix d'options complexes, y compris les options américaines qui peuvent être exercées à tout moment.

Outil de gestion du risque

• Ils permettent aux traders d'évaluer et de couvrir les risques en simulant divers scénarios de marché et résultats d'options.

Applicable à tous les actifs

• Ces modèles sont polyvalents et utiles pour les actions, les taux d'intérêt et les dérivés de crédit.

Exemple de codage

• Nous présentons ci-dessous un exemple de codage Python d'un modèle de treillis (arbre binomial).

Voici un aperçu de leurs applications dans les domaines de la finance, des marchés et de la négociation :

Modèles d'évaluation des options en treillis

Arbres binomiaux et trinomiaux

Il s'agit des modèles de treillis les plus couramment utilisés pour l'évaluation des options.

Le modèle binomial décompose le délai d'expiration d'une option en un nombre potentiellement élevé d'intervalles de temps, ou étapes.

À chaque étape, le prix peut augmenter ou diminuer d'un facteur spécifique.

Les arbres trinomiaux étendent ce concept en autorisant trois mouvements possibles : à la hausse, à la baisse ou sans changement.

Des exemples de codage d'arbres binomiaux sont présentés à la fin de cet article.

Flexibilité de la modélisation

Les arbres binomiaux sont très utiles pour les options de type américain, qui peuvent être exercées à tout moment avant l'expiration, car ils peuvent facilement prendre en compte les caractéristiques de l'option qui dépendent de la trajectoire.

Modèles de treillis de taux d'intérêt

Modélisation des prix et des rendements des obligations

Les modèles de treillis peuvent simuler l'évolution des taux d'intérêt dans le temps.

Cela permet d'évaluer les produits dérivés sur les taux d'intérêt, tels que les options sur obligations, les caps et les floors.

Modèles Hull-White et Black-Derman-Toy

Ce sont des exemples de modèles de treillis appliqués aux mouvements des taux d'intérêt.

Modèles de treillis dans la modélisation du risque de crédit

Estimation de la probabilité de défaut

Ils sont utilisés pour estimer la probabilité de défaut d'un émetteur d'obligations ou d'une contrepartie dans une transaction de produits dérivés.

Exposition au risque de crédit

Utile pour calculer l'exposition future potentielle des positions dérivées.

Prend en compte les défaillances possibles.

Modèles de treillis dans l'analyse des options réelles et les décisions de financement des entreprises

Utilisés pour analyser les décisions d'investissement dans des actifs réels, où l'optionalité découle de la capacité de la direction à prendre des décisions futures qui affectent la valeur du projet ou de l'investissement.

Modèles de treillis dans la gestion de portefeuille et l'allocation d'actifs

Allocation stratégique

Peut être utilisé pour modéliser le comportement des prix des actifs dans différents scénarios économiques.

Aide à l'allocation stratégique des actifs.

Gestion du risque

Aide à évaluer le profil de risque d'un portefeuille dans différentes conditions de marché.

Modèles de treillis et simulations de marché

Les treillis peuvent être une alternative aux simulations Monte Carlo pour modéliser le comportement des prix des actifs, en particulier lorsqu'il s'agit d'options dépendantes de la trajectoire ou de produits dérivés complexes.

Les mathématiques des modèles de treillis

Voici un bref aperçu des mathématiques qui sous-tendent les modèles de treillis pour l'évaluation des options :

L'idée de base est de discrétiser les processus stochastiques continus de modèles tels que Black-Scholes dans une structure de treillis ou d'arbre (c'est-à-dire de les diviser en très petites étapes).

Quelques équations clés

Le prix de l'actif à chaque nœud suit une distribution binomiale* :

• S(t+Δt) = S(t)u, avec une probabilité p

• S(t+Δt) = S(t)d, avec une probabilité de 1 - p

Où u et d sont les facteurs de hausse et de baisse :

• u = e^σ√Δt

• d = 1/u

Les probabilités de transition neutres à l'égard du risque sont les suivantes :

• p = (R - d)/(u - d)

• 1 - p = (u - R)/(u - d)

Où R est le taux sans risque sur la période Δt.

Les paramètres u, d et p sont calibrés sur des données réelles.

Le prix de l'option est calculé à rebours des nœuds finaux à l'aide de l'évaluation risque-neutre :

• C(t) = (p*C(t+Δt, up) + (1-p)*C(t+Δt, down))/R

Où C(t) est le prix de l'option au moment t, et C(t+Δt, up) et C(t+Δt, down) sont les prix de l'option aux nœuds up et down à t+Δt.

En remontant l'arbre, le prix initial de l'option C(0) peut être calculé.

Le treillis fournit une approximation discrète du processus continu.

Il existe différentes formules en fonction du type d'option (call/put) et du moment de l'exercice (européen/américain).

*(Il convient de noter que l'hypothèse d'une distribution binomiale ne s'applique qu'à la variation du prix de l'actif. La distribution réelle du prix de l'actif ne sera pas parfaitement binomiale).

Avantages des modèles en treillis

Flexibilité

Ils peuvent être adaptés à différents types de produits dérivés et d'actifs sous-jacents.

Efficacité de calcul

Généralement plus efficaces que les modèles continus pour les options de type américain et les options exotiques.

Limites des modèles en treillis

Simplicité et réalité

Le mouvement simpliste haut/bas peut ne pas refléter les complexités réelles des marchés financiers.

Erreurs de discrétisation

Comme ils discrétisent le temps et les mouvements de prix, il peut y avoir des erreurs par rapport aux modèles continus.

Nombre limité de trajectoires discrètes

Les modèles en treillis ne suivent qu'un certain nombre de trajectoires discrètes.

Alternatives aux modèles de treillis

Les alternatives aux modèles de treillis sur les marchés financiers sont les suivantes :

Modèle de Black-Scholes

Un modèle à temps continu pour l'évaluation des options européennes.

Le modèle de Black-Scholes est une solution fermée qui simplifie les calculs, mais qui peut ne pas traiter avec précision les options américaines ou les caractéristiques dépendant de la trajectoire.

Simulations de Monte Carlo

Utilisées pour fixer le prix de produits dérivés complexes et évaluer le risque en simulant des milliers de trajectoires futures potentielles pour les prix des actifs.

Elles intègrent un large éventail de conditions de marché.

Méthodes de différences finies

Techniques numériques permettant de résoudre les équations différentielles apparaissant dans l'évaluation des options.

Utile pour une variété d'options exotiques et capable de traiter des caractéristiques d'exercice de type américain.

Modèles de volatilité locale

Étendent le cadre de Black-Scholes en permettant à la volatilité de varier à la fois en fonction du temps et du prix de l'actif sous-jacent.

Résumé

Ces méthodes présentent différents avantages, de l'efficacité informatique à la capacité de modéliser des comportements de marché complexes.

Elles fournissent aux traders quantiques et aux ingénieurs financiers une boîte à outils pour divers scénarios.

Développements récents et intégration de l'IA

Intégration avec l'apprentissage automatique

L'IA et l'apprentissage automatique sont utilisés pour améliorer les modèles de treillis, en particulier pour calibrer plus efficacement les paramètres du modèle.

Trading à haute fréquence

Dans le cadre du trading algorithmique et à haute fréquence, les modèles de treillis peuvent être intégrés dans des stratégies de tarification et de gestion des risques.

Exemple de codage - Modèles de treillis

Le modèle d'arbre binomial est un modèle à temps discret utilisé pour l'évaluation des options, et communément utilisé pour les options américaines, qui peuvent être exercées à tout moment avant l'expiration.

Le modèle fonctionne en divisant le temps jusqu'à l'expiration en un certain nombre d'intervalles discrets, ou étapes.

À chaque étape, le prix de l'action peut augmenter ou diminuer d'un certain facteur, et la valeur de l'option est calculée à rebours depuis l'expiration jusqu'à aujourd'hui.

Vous trouverez ci-dessous une simple implémentation Python d'un modèle d'arbre binomial pour une option d'achat européenne.

Nous utiliserons une option européenne pour des raisons de simplicité, car son évaluation ne nécessite pas de vérifier l'existence d'un exercice anticipé à chaque étape (contrairement à une option américaine).

Néanmoins, la logique est assez similaire et peut facilement être étendue aux options américaines avec des modifications mineures.

import numpy as np

def binomial_tree_call_option(S0, K, T, r, sigma, N):
"""
Price a European call option using the binomial tree model.

Parameters:
S0 : float
Initial stock price
K : float
Strike price of the option
T : float
Time to maturity in years
r : float
Risk-free interest rate
sigma : float
Volatility of the underlying asset
N : int
Number of steps in the binomial tree

Returns:
float
Price of the European call option
"""
# Calculate delta T
deltaT = T / N

# Calculate up and down factors
u = np.exp(sigma * np.sqrt(deltaT))
d = 1 / u

# Calculate risk-neutral probability
p = (np.exp(r * deltaT) - d) / (u - d)

# Initialize our array for stock prices
stock_price = np.zeros((N + 1, N + 1))
stock_price[0, 0] = S0

for i in range(1, N + 1):
stock_price[i, 0] = stock_price[i - 1, 0] * u
for j in range(1, i + 1):
stock_price[i, j] = stock_price[i - 1, j - 1] * d

# Initialize the option value at maturity
option_value = np.zeros((N + 1, N + 1))
for j in range(N + 1):
option_value[N, j] = max(0, stock_price[N, j] - K)

# Iterate backwards in time to calculate the option price
for i in range(N - 1, -1, -1):
for j in range(i + 1):
option_value[i, j] = (p * option_value[i + 1, j] + (1 - p) * option_value[i + 1, j + 1]) / np.exp(r * deltaT)

return option_value[0, 0]

# Example parameters
S0 = 100 # Initial stock price
K = 100 # Strike price
T = 1 # Time to maturity in years
r = 0.05 # Risk-free interest rate
sigma = 0.2 # Volatility
N = 50 # Number of steps

# Calculate the call option price
call_price = binomial_tree_call_option(S0, K, T, r, sigma, N)
print(f"The European call option price is: {call_price}")

Ce script définit une fonction binomial_tree_call_option pour calculer le prix d'une option d'achat européenne à l'aide du modèle de l'arbre binomial.

Vous pouvez ajuster les paramètres (S0, K, T, r, sigma, N) en fonction de l'option spécifique que vous souhaitez évaluer.

Le modèle commence par construire un arbre binomial pour le prix de l'action sous-jacente sur N étapes jusqu'à l'expiration, puis calcule la valeur de l'option à chaque nœud en commençant par l'expiration et en remontant jusqu'à aujourd'hui.

La probabilité neutre vis-à-vis du risque p est utilisée pour pondérer les gains attendus dans le futur, actualisés au taux sans risque r.

Graphique du modèle d'arbre binomial

Voici un code que nous pouvons utiliser pour générer un graphique du modèle de l'arbre binomial afin de simuler la trajectoire du prix d'une action au fil du temps.

import matplotlib.pyplot as plt

def plot_binomial_tree(S0, K, T, r, sigma, N):
"""

Parameters:
S0 : float
Initial stock price
K : float
Strike price of the option
T : float
Time to maturity in years
r : float
Risk-free interest rate
sigma : float
Volatility of the underlying asset
N : int
Number of steps in the binomial tree
"""
deltaT = T / N
u = np.exp(sigma * np.sqrt(deltaT))
d = 1 / u
p = (np.exp(r * deltaT) - d) / (u - d)

# Stock price tree
stock_price = np.zeros((N + 1, N + 1))
for i in range(N + 1):
for j in range(i + 1):
stock_price[i, j] = S0 * (u ** j) * (d ** (i - j))

# Option value tree
option_value = np.zeros((N + 1, N + 1))
for j in range(N + 1):
option_value[N, j] = max(0, stock_price[N, j] - K)
for i in range(N - 1, -1, -1):
for j in range(i + 1):
option_value[i, j] = (p * option_value[i + 1, j] + (1 - p) * option_value[i + 1, j + 1]) / np.exp(r * deltaT)

# Plotting
plt.figure(figsize=(10, 6))
for i in range(N + 1):
for j in range(i + 1):
if i < N:
plt.plot([i, i + 1], [stock_price[i, j], stock_price[i + 1, j]], color='gray', lw=1)
plt.plot([i, i + 1], [stock_price[i, j], stock_price[i + 1, j + 1]], color='gray', lw=1)
plt.scatter(i, stock_price[i, j], color='blue', s=10) # Stock price nodes

# Highlight option valuation at maturity
for j in range(N + 1):
if stock_price[N, j] - K > 0:
plt.scatter(N, stock_price[N, j], color='red', s=30) # In-the-money nodes at expiration

plt.title("Binomial Tree Model of Stock Price and Option Valuation at Expiration")
plt.xlabel("Time Steps")
plt.ylabel("Stock Price")
plt.grid(True)
plt.show()

# Plot the binomial tree with option valuation
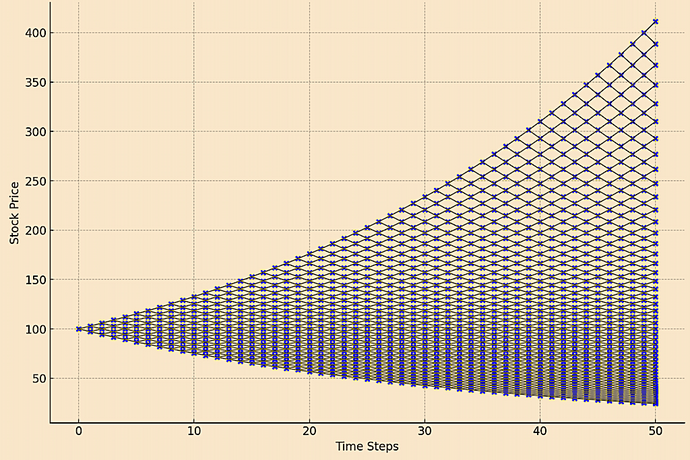
plot_binomial_tree(S0=100, K=100, T=1, r=0.05, sigma=0.2, N=50)

Voici le graphique montrant la trajectoire du modèle binomial pour le prix de l'action au fil du temps, selon les paramètres spécifiés.

Chaque nœud représente un prix possible de l'action à ce moment-là.

Vous pouvez remarquer le format en treillis qui illustre comment le prix de l'action peut évoluer à travers le modèle binomial jusqu'à l'expiration, avec une large distribution de résultats possibles.

Cette visualisation permet de comprendre la dynamique de l'évaluation des options dans le cadre du modèle binomial.

Modèle d'arbre binomial du prix de l'action

Conclusion

Les modèles de treillis restent un élément fondamental de la modélisation et de l'analyse financières.

Ils offrent un mélange de rigueur théorique et d'applicabilité pratique dans divers domaines de la finance.

Leur adaptabilité et leur efficacité les rendent utiles aux professionnels des marchés financiers et du trading.

Brokers d'options

Investir comporte des risques de perte

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.