#1 03-07-2024 12:58:05

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 231

La structure par termes des volatilités implicites

Le trading sur la structure par termes des volatilités implicites implique (STVI) des stratégies qui tirent parti des différences de volatilité implicite entre les différentes échéances des options sur le même actif sous-jacent.

Elle fait référence à la relation entre les volatilités implicites des options ayant le même actif sous-jacent mais des dates d'expiration différentes.

Points clés :

➡️ La structure par terme de la volatilité est une variation de la volatilité implicite entre les différentes échéances des options (reflétant les attentes du marché en matière de volatilité).

➡️ Exploiter les différences de volatilité - Utiliser les variations de la volatilité implicite entre les différentes échéances pour générer des profits.

➡️ Gestion du risque - Il est essentiel de surveiller les grecques, en particulier le vega et le gamma, afin d'équilibrer l'exposition.

Concepts clés

Volatilité implicite (IV)

• Définition - La volatilité implicite représente les attentes du marché concernant la volatilité de l'actif sous-jacent pendant la durée de vie de l'option.

• Calcul - Elle est dérivée du prix de marché de l'option à l'aide de modèles tels que Black-Scholes.

Structure par termes de la volatilité

• Définition - Cette structure illustre la façon dont la volatilité implicite varie pour des options ayant des échéances différentes.

• Forme - Elle peut prendre différentes formes (pente ascendante, pente descendante, bosse, etc.), reflétant les attentes du marché quant à la volatilité future.

Stratégies de trading

Spreads calendaires

Il s'agit d'acheter et de vendre des options ayant des dates d'expiration différentes mais le même prix d'exercice.

Types d'écarts

• Spread horizontal - Même prix d'exercice, différentes échéances.

• Spread diagonal - Différents prix d'exercice et différentes échéances.

Objectif

Profiter des changements dans la structure à terme de la volatilité.

Par exemple, si l'on s'attend à ce que la volatilité du premier mois diminue par rapport à la volatilité à plus long terme, les traders peuvent vendre des options à court terme et acheter des options à plus long terme.

Arbitrage de volatilité

Exploitation des différences entre la volatilité implicite et la volatilité réalisée ou entre les volatilités implicites de différentes échéances.

Techniques

• Stratégies Delta-Neutre - Construire des positions qui sont neutres par rapport à la direction de l'actif sous-jacent mais exposées aux changements de volatilité.

• Positions pondérées en fonction de la valeur Véga - Se concentrer sur la sensibilité du portefeuille aux variations de la volatilité.

Stratégies gamma long/court

• Gamma long - consiste à acheter des options pour profiter des hausses de volatilité.

• Gamma court - consiste à vendre des options pour profiter de la baisse de la volatilité implicite ou pour capturer la prime.

Gestion des risques

Asymétrie et sourire de la volatilité

• Asymétrie - Modèle dans lequel les options hors de l'argent (OTM) ont des volatilités implicites différentes de celles des options à l'argent (ATM).

• Sourire - Une distorsion symétrique où les options d'achat et de vente OTM profondes ont des volatilités implicites plus élevées que les options ATM.

• Impact sur la stratégie - Il est important de comprendre l'asymétrie et le sourire car ils ont un impact sur le prix des options et sur la rentabilité des stratégies de structure des échéances de la volatilité.

Grecques

• Delta - Mesure la sensibilité du prix de l'option aux variations du prix de l'actif sous-jacent.

• Gamma - Mesure le taux de variation du delta par rapport au prix de l'actif sous-jacent.

• Vega - Mesure la sensibilité du prix de l'option aux variations de la volatilité.

• Thêta - Mesure la décroissance temporelle du prix de l'option.

Voir aussi : grecques d'options

Application pratique

Évaluer les conditions du marché

Identifier la forme de la STVI et les attentes du marché en matière de volatilité.

Construire des positions

Développer des spreads calendaires ou des positions d'arbitrage de volatilité sur la base de la forme de la STVI.

Surveiller les effets des grecques

S'assurer que les expositions au risque du portefeuille sont gérées, en particulier le vega et le gamma.

Ajuster les positions

Ajuster dynamiquement les positions en fonction de l'évolution des marchés et de la structure à terme de la volatilité.

Exemple d'opération sur la structure par terme de la volatilité

Considérons un scénario dans lequel la STVI est en pente ascendante, indiquant une volatilité future plus élevée, mais où un trader estime que cette volatilité future est encore sous-évaluée (c'est-à-dire qu'elle devrait être encore plus élevée).

Il pourrait alors:

• Acheter des options à plus long terme (par exemple, six mois avant l'expiration) pour profiter des augmentations attendues de la volatilité.

• Vendre des options à plus court terme (par exemple, un mois avant l'échéance) pour capter la prime, en pariant que la volatilité à court terme restera inférieure à ce qu'impliquent les prix actuels.

Couverture delta

Pour isoler la volatilité et minimiser le risque directionnel, le trader utilise la couverture delta.

Le delta mesure la sensibilité d'une option aux variations du prix de l'actif sous-jacent. Voici comment le trader peut couvrir le delta dans le cadre de cette stratégie :

1) Calculer le delta

Déterminez le delta de l'option à long terme et de l'option à court terme.

Supposons que:

• l'option à long terme a un delta de 0,5 et

• l'option à court terme a un delta de 0,3

2) Delta net

Calculez le delta net de la position combinée.

Par exemple, si le trader achète une option à long terme et vend une option à court terme, le delta net est de 0,5 - 0,3 = 0,2.

3) Delta de couverture

Pour neutraliser ce delta, le trader prend une position opposée sur l'actif sous-jacent.

Dans ce cas, il vendra 0,2 unité de l'actif sous-jacent pour chaque écart créé.

4) Ajuster en continu

Lorsque le prix de l'actif sous-jacent varie, les deltas des options changent également. Le trader devra ajuster en permanence sa position sur l'actif sous-jacent afin de maintenir une position delta-neutre.

Dans l'ensemble

En couvrant le delta, le trader isole efficacement l'exposition de la position aux changements de volatilité.

Il peut ainsi profiter de l'augmentation attendue de la volatilité à long terme sans être affecté par les mouvements de prix de l'actif sous-jacent.

Surface de volatilité

Une surface de volatilité est un graphique tridimensionnel qui visualise la volatilité implicite des options pour différents prix d'exercice et différentes échéances pour un actif sous-jacent donné.

Elle offre une vue d'ensemble de la manière dont la volatilité implicite, une donnée importante dans la détermination du prix des options, varie selon les deux dimensions.

Composants clés

Prix d'exercice (axe X)

Le prix auquel l'option peut être exercée.

Les options peuvent être dans la monnaie, à la monnaie ou hors de la monnaie, en fonction du prix d'exercice par rapport au prix actuel de l'actif sous-jacent.

Échéance (axe des ordonnées)

Temps restant jusqu'à l'expiration de l'option, généralement mesuré en jours, mois ou années.

Volatilité implicite (axe Z)

Attentes du marché concernant la volatilité de l'actif sous-jacent pendant la durée de vie de l'option.

La volatilité implicite est dérivée du prix de marché de l'option à l'aide de modèles tels que Black-Scholes.

Diagramme de surface de volatilité

Nous pouvons concevoir un diagramme d'une surface de volatilité en créant des tableaux et en les traçant :

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

# Exemple de données pour une structure par terme de la volatilité en trois dimensions

strikes = np.array([50, 55, 60, 65, 70])

maturities = np.array([30, 90, 180, 365, 730])

implied_vols = np.array([

[0.20, 0.18, 0.15, 0.14, 0.13],

[0.22, 0.20, 0.18, 0.17, 0.16],

[0.25, 0.22, 0.20, 0.19, 0.18],

[0.28, 0.25, 0.22, 0.21, 0.20],

[0.30, 0.27, 0.24, 0.23, 0.22]

])

# Grille de maillage pour le traçage

X, Y = np.meshgrid(strikes, maturities)

Z = implied_vols

# Tracer la structure par terme de la volatilité en 3D

fig = plt.figure(figsize=(12, 8))

ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(X, Y, Z, cmap='viridis')

ax.set_title('3D Volatility Term Structure')

ax.set_xlabel('Strike Price')

ax.set_ylabel('Maturity (Days)')

ax.set_zlabel('Implied Volatility')

plt.show()

Surface de volatilité en 3D

Formes de la surface de volatilité

Sourire de la volatilité

Souvent observé dans les options sur actions, où les volatilités implicites sont plus élevées pour les options profondément dans la monnaie et hors de la monnaie que pour les options dans la monnaie.

Elle forme un U lorsqu'elle est représentée par rapport aux prix d'exercice pour une échéance fixe.

Par exemple :

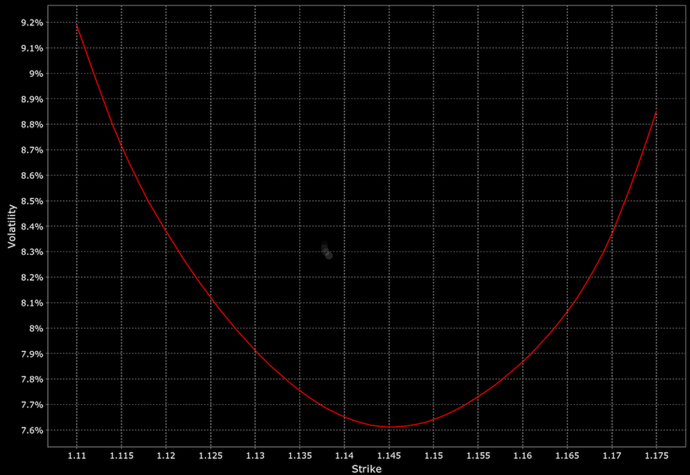
Asymétrie de la volatilité

Implique un schéma systématique dans lequel les volatilités implicites varient en fonction des prix d'exercice, souvent plus élevées pour les prix d'exercice inférieurs (options de vente) ou supérieurs (options d'achat).

Cela reflète le sentiment du marché et les pressions de couverture.

Voici deux exemples :

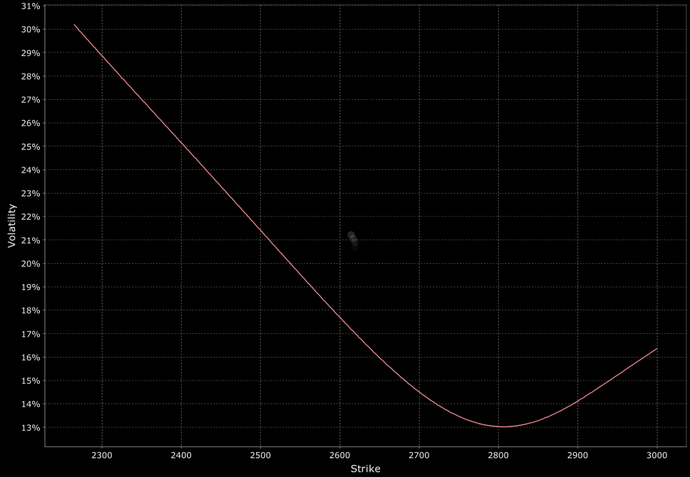
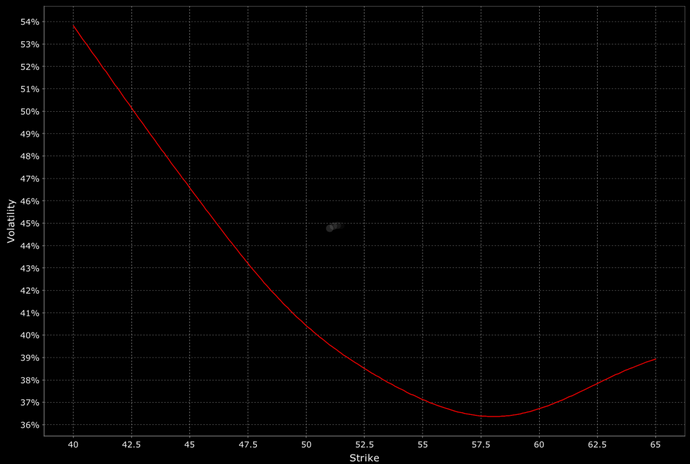
Structure par terme de la volatilité

La structure de la volatilité implicite entre les différentes échéances.

Elle peut être ascendante (impliquant une volatilité future plus élevée) ou descendante (impliquant une volatilité future plus faible).

Applications pratiques

Gestion du risque

Les traders utilisent la surface de volatilité pour comprendre le coût relatif des options et pour couvrir les portefeuilles.

La compréhension de la surface permet d'élaborer des stratégies de couverture plus efficaces.

Stratégies de tarification et de trading

En analysant la surface de volatilité, les traders peuvent identifier les options mal évaluées et mettre en œuvre des stratégies telles que l'arbitrage de volatilité, les spreads calendaires et les straddles.

Calibration des modèles

La surface de volatilité est essentielle pour calibrer les modèles d'évaluation des options afin de s'assurer qu'ils reflètent correctement les conditions du marché.

Des modèles comme le SABR ou les modèles de volatilité stochastique sont souvent utilisés à cette fin.

Construction de la surface de volatilité

La surface de volatilité est construite à l'aide de données de marché pour les prix des options pour différents prix d'exercice et échéances.

Des techniques sophistiquées d'interpolation et d'extrapolation sont utilisées pour combler les lacunes lorsque les données du marché sont rares, afin d'obtenir une surface lisse et continue.

Autres concepts

Structure par terme de la volatilité de la volatilité

La structure à terme de la volatilité de la volatilité représente la variation de la volatilité de la volatilité implicite pour différentes échéances d'options.

Elle donne un aperçu des attentes du marché quant à l'incertitude de la volatilité future.

Elle aide les traders et les gestionnaires de risques à mieux comprendre le potentiel d'évolution significative de la volatilité au fil du temps.

Le VVIX (volatilité du VIX) est l'indicateur le plus populaire de la structure à terme de la volatilité.

Sources de l'article

[*]Modélisation de la structure par terme en cas d'incertitude sur la volatilité[/*]
[*]Structure par terme de la volatilité implicite et prévisibilité des taux de change[/*]

Brokers d'options

Investir comporte des risques de perte

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.