Analyse en composantes principales (applications de trading)

Climax · 09-02-2024 12:29:06

Analyse en composantes principales (applications de trading et d'investissement)

L'analyse en composantes principales (ACP) est une méthode statistique utilisée pour simplifier la complexité des ensembles de données à haute dimension en réduisant la dimensionnalité.

Cette technique transforme les variables d'origine en un nouvel ensemble de variables - appelées composantes principales - qui ne sont pas corrélées et sont ordonnées de telle sorte que les premières conservent la plupart des variations présentes dans les variables d'origine.

Principaux enseignements :

L'analyse en composantes principales (ACP) réduit la complexité des données de marché.
Elle identifie les facteurs sous-jacents qui déterminent les mouvements de prix des actifs.
Elle permet aux traders de se concentrer sur ce qui est le plus important dans les données.
L'ACP permet d'optimiser les portefeuilles en isolant les principaux facteurs de rendement.

Applications de l'ACP dans le domaine du trading et de l'investissement

Diversification des portefeuilles et gestion des risques

L'ACP permet d'identifier les facteurs sous-jacents qui déterminent les rendements d'un portefeuille.

Les traders/investisseurs utilisent l'ACP pour comprendre l'exposition au risque de leur portefeuille à divers facteurs de marché.

En identifiant ces facteurs, ils peuvent ajuster leur portefeuille pour atteindre le niveau de risque souhaité.

L'ACP permet également d'éliminer les détails inutiles sur lesquels il n'est pas important de se concentrer.

Par exemple, un fonds de pension sait que les variations des prix du pétrole affectent son portefeuille.

Mais il sait aussi que ce n'est pas important tant qu'il est suffisamment diversifié et qu'il n'a pas besoin d'avoir une vision tactique de la matière première.

Analyse du marché et développement de la stratégie

Les traders utilisent l'ACP pour trouver des modèles dans les mouvements de prix des actifs.

Cette méthode est utile dans le cadre du trading algorithmique, où l'identification rapide des tendances du marché et des corrélations peut déboucher sur de bonnes stratégies.

L'ACP permet de simplifier les données du marché.

Elle permet aux traders de se concentrer sur les composantes principales qui ont un impact significatif sur les prix des actifs.

Par exemple, nous avons mentionné qu'au niveau macroéconomique, les prix des actifs sont principalement déterminés par les changements de quatre variables principales :

la croissance actualisée
l'inflation actualisée
les taux d'actualisation
les primes de risque

Bien qu'il existe de nombreux autres facteurs qui influencent les prix des actifs (en particulier au fur et à mesure que l'on descend dans les niches), ces variables sont considérées comme les principales composantes des moteurs des actifs et des portefeuilles au niveau macroéconomique.

Analyse de la courbe de rendement

L'ACP est largement utilisée pour analyser les courbes de rendement, qui sont importantes pour les investissements à revenu fixe.

Les quelques premières composantes principales peuvent expliquer le niveau, la pente et la courbure des courbes de rendement.

La compréhension de ces composantes aide les traders à prévoir les variations des taux d'intérêt et à prendre des décisions de qualité sur les marchés des obligations et des taux.

Modèles factoriels améliorés

Dans la recherche sur les actions, l'ACP est appliquée pour construire des modèles factoriels.

Elle permet d'identifier les facteurs qui expliquent les rendements d'une action ou d'un portefeuille.

Voici quelques exemples :

la taille
le momentum
la qualité
la valeur

En se concentrant sur ces facteurs, les analystes peuvent créer des modèles qui capturent mieux la dynamique des rendements boursiers.

Avantages de l'utilisation de l'ACP dans les transactions et les investissements

Réduction de la dimensionnalité

L'ACP réduit le nombre de variables, ce qui rend l'analyse plus facile à gérer.

Elle est particulièrement utile lorsqu'il s'agit de traiter de grands ensembles de données, ce qui est courant sur les marchés financiers.

Étant donné que l'analyse des données sur les marchés devient de plus en plus complexe et qu'elle est analysée selon de nouvelles méthodes (par exemple, la théorie des tenseurs, la géométrie de l'information, la géométrie différentielle), les techniques de réduction de la dimensionnalité permettent de rendre l'analyse plus gérable.

Réduction du bruit

L'ACP permet de filtrer le bruit et de se concentrer sur les variables qui contribuent le plus à la variance de l'ensemble de données.

Cela permet d'obtenir des modèles et des prédictions plus précis.

Visualisation perspicace des données

La réduction de la dimensionnalité des données à deux ou trois composantes principales permet une visualisation efficace (puisque nous ne pouvons réellement visualiser que trois composantes sur un graphique).

Cela permet d'identifier des modèles et des relations qui ne sont pas apparents dans les données à haute dimension.

Amélioration des performances des modèles algorithmiques

L'ACP peut améliorer les performances des modèles d'apprentissage automatique en réduisant l'ajustement excessif.

L'ensemble réduit de variables limite la complexité du modèle, ce qui le rend souvent plus généralisable à de nouvelles données.

Limites et considérations de l'APC

Perte d'informations

Si l'ACP réduit la dimensionnalité, elle élimine également certaines informations.

Les composantes éliminées peuvent contenir des informations importantes pour certaines analyses ou stratégies commerciales.

En général, l'idée qui sous-tend l'ACP est que les avantages de la réduction de la dimensionnalité l'emportent sur la perte d'informations afin de rendre l'analyse financière plus facile à réaliser.

Interprétabilité

Les composantes principales sont des combinaisons linéaires des variables originales et peuvent être difficiles à interpréter.

Cette nature abstraite peut être un inconvénient lorsqu'on essaie de comprendre les facteurs qui sous-tendent les composantes.

Sensibilité aux valeurs aberrantes

L'ACP est sensible aux valeurs aberrantes des données.

Les valeurs aberrantes peuvent fausser les résultats et conduire à des interprétations trompeuses.

Un prétraitement soigneux des données est essentiel pour éviter ce problème.

Hypothèse de linéarité

L'ACP suppose que les composantes principales sont une combinaison linéaire des variables originales.

Cela peut ne pas être le cas sur des marchés financiers complexes où les relations entre les variables sont souvent non linéaires.

Les mathématiques de l'analyse en composantes principales (ACP)

Étant donné un ensemble de données X composé de n observations et de p variables, l'ACP vise à trouver k vecteurs de composantes principales qui capturent les directions de la variance maximale.

Modéliser les données par une transformation linéaire :

[*]X = TP' + E[/*]

où :

T est une matrice n x k des scores des composantes principales
P est une matrice p x k des charges des composantes principales
E est le bruit résiduel

Trouver P pour maximiser la variance de T :

Var(Tp) = P'SBP
Sous réserve de : PT*P = I

Où : Sb est la matrice de covariance de X

Sb est la matrice de covariance de X
I est la matrice d'identité

En prenant la décomposition des valeurs propres :

Sb = VΛV'

Les colonnes de V correspondant aux k premières valeurs propres sont les directions des composantes principales P.

La projection des données sur P donne les scores des composantes T. Un petit nombre de composantes peut approximer X en reconstruisant TP'.

Résumé

L'ACP utilise la factorisation matricielle pour transformer linéairement les données et maximiser la variance, révélant ainsi la structure latente. La décomposition des valeurs propres fournit une solution informatique élégante.

Exemple de codage - ACP

Dans un autre article, nous avons examiné l'utilisation des manifolds de Riemann dans la géométrie différentielle pour l'optimisation des portefeuilles et la façon dont ils représentent les données financières sur des manifolds où la courbure et la topologie sont utiles pour comprendre les relations entre les données et aider à optimiser les portefeuilles.

Il pourrait s'agir d'exemples que nous pourrions essayer de réduire dans un cadre 2D de moyenne-variance à l'aide de l'ACP pour plus de simplicité.

Pour cet exemple, prenons l'exemple d'un manifold symplectique et réduisons-le de 3D à 2D pour plus de simplicité à l'aide de l'ACP.

La forme 3D :

Manifold symplectique en 3D

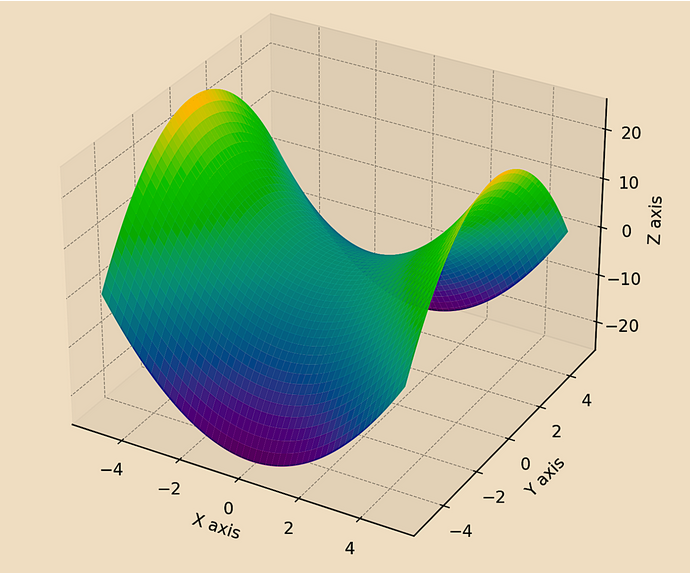
La forme 2D :

Manifold symplectique réduit par l'ACP en 2D

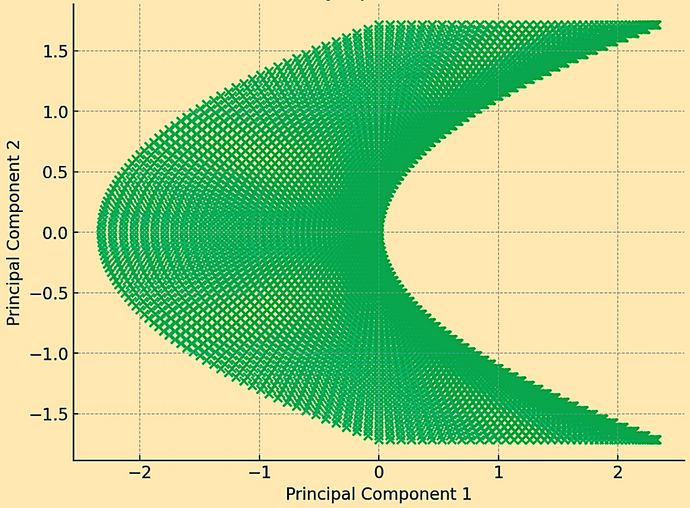
Le nuage de points montre comment le manifold, initialement en trois dimensions, est projeté sur deux composantes principales.

Ce processus permet de capturer l'essence de la structure du collecteur, en se concentrant sur les directions de variance les plus significatives.

En réduisant la dimensionnalité, l'ACP fournit une vue simplifiée qui peut être plus facilement analysée tout en conservant les caractéristiques clés du manifold original.

Le code pour ce faire :

from sklearn.decomposition import PCA

# Define a grid
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)

# Define a symplectic form, e.g., a simple saddle as an example
z = x**2 - y**2

# Flatten the grid and z values for PCA
X_flat = x.flatten()
Y_flat = y.flatten()
Z_flat = z.flatten()

# Combine into a single data structure
data = np.vstack((X_flat, Y_flat, Z_flat)).T

# Standardize the data before applying PCA
scaler = StandardScaler()
data_standardized = scaler.fit_transform(data)

# Apply PCA
pca = PCA(n_components=2)
data_reduced = pca.fit_transform(data_standardized)

# Plot the reduced data
plt.figure(figsize=(8, 6))
plt.scatter(data_reduced[:, 0], data_reduced[:, 1], alpha=0.6, cmap='viridis')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('PCA Reduced Symplectic Manifold to 2D')
plt.grid(True)
plt.show()

Alternatives à l'ACP

Quelques alternatives à l'analyse ACP :

t-Distributed Stochastic Neighbor Embedding (t-SNE) (intégration des voisins stochastiques distribués)

Efficace pour visualiser des données de haute dimension dans des dimensions inférieures (en particulier en 2D ou 3D) en conservant les structures de données locales.

Analyse en composantes indépendantes (ICA)

Se concentre sur la séparation d'un signal multivarié en composantes additives et indépendantes.

Utile pour le traitement des signaux et l'analyse des séries temporelles.

Analyse factorielle (AF)

Identifie les variables sous-jacentes (facteurs) qui expliquent les corrélations observées entre les variables.

Approximation et projection uniformes du milieu (UMAP)

Technique de réduction de la dimensionnalité qui maintient la structure globale des données.

Utile pour les grands ensembles de données et plus apte à préserver la structure globale que t-SNE.

Conclusion

L'ACP simplifie la complexité inhérente aux marchés financiers, ce qui permet une analyse plus ciblée et plus efficace.

Bien qu'elle comporte certaines limites, ses avantages en matière de gestion des risques, d'analyse des marchés et de construction de modèles en font une technique importante et largement utilisée dans le domaine de la finance quantitative.

Comme toute méthode analytique, elle doit être utilisée judicieusement et en conjonction avec d'autres outils et connaissances du domaine pour obtenir les meilleurs résultats.

#1 09-02-2024 12:29:06