Théorie des réseaux et percolation en finance

Climax · 17-02-2024 21:12:42

Théorie des réseaux et percolation en finance et trading

La théorie des réseaux et les modèles de percolation permettent de comprendre divers phénomènes financiers et boursiers.

Ces concepts, dérivés des mathématiques et de la physique, fournissent des cadres quantitatifs pour l'interconnexion et les vulnérabilités des marchés financiers.

Nous examinons ci-dessous les concepts clés, les applications et la manière dont les traders peuvent tirer parti de la théorie des réseaux et de la percolation dans leurs stratégies.

Les mathématiques qui sous-tendent la théorie des réseaux et la percolation s'appuient sur la théorie des graphes, l'algèbre linéaire et matricielle, la théorie des probabilités, la théorie des groupes, les processus stochastiques et la mécanique statistique pour étudier les réseaux complexes du monde réel.

L'accent est mis sur la topologie et les modèles qui émergent des interactions entre les nœuds locaux.

Principaux enseignements :

Analyse de l'interconnexion

La théorie des réseaux en finance met en évidence l'interconnexion des institutions financières et des marchés.
Les traders doivent être conscients que les actifs ne sont pas isolés.
L'échec ou le succès de l'un d'entre eux peut rapidement en affecter d'autres, un peu comme l'effet domino dans les systèmes en réseau.

Identification du risque systémique

La théorie de la percolation permet d'identifier les seuils à partir desquels une détresse financière localisée peut dégénérer en crise systémique.
La compréhension de ces points de basculement permet aux opérateurs de mieux évaluer et de réduire les risques systémiques dans leurs portefeuilles.

Stratégie de diversification des portefeuilles

L'analyse de la structure en réseau des marchés financiers permet aux opérateurs de concevoir de meilleures stratégies de diversification qui tiennent compte des corrélations cachées et du potentiel de contagion (et qui améliorent la résistance des portefeuilles aux chocs du marché).

Concepts clés de la théorie des réseaux

La théorie des réseaux se concentre sur l'étude des graphiques en tant que représentations des relations et des interactions dans un système complexe.

En finance, les réseaux peuvent représenter diverses entités (individus, institutions, marchés ou pays) et les liens qui les unissent (transactions financières, dépendances ou corrélations).

Les nœuds

Les nœuds représentent les entités du réseau, telles que les banques, les institutions financières, les actifs ou les marchés.

Arêtes

Les arêtes représentent les connexions ou les relations entre ces entités, telles que les prêts, la propriété ou les relations commerciales.

Mesures de centralité

Les mesures de centralité évaluent l'importance d'un nœud au sein du réseau, ce qui peut être révélateur d'un risque systémique ou d'une influence.

Coefficient de regroupement

Le coefficient de regroupement mesure le degré auquel les nœuds d'un réseau ont tendance à se regrouper.

Il met en évidence les risques potentiels de segmentation ou de concentration du marché.

Théorie de la percolation

La théorie de la percolation est un cadre mathématique utilisé pour étudier le comportement des grappes connectées dans un graphe aléatoire.

En finance, elle permet de modéliser la diffusion d'informations, de crises ou de défaillances à travers un réseau.

Elle examine comment de petits changements peuvent avoir des effets étendus en raison de l'interconnexion du système.

Modèles de seuil

Les modèles de seuil sont utilisés dans la théorie de la percolation pour déterminer le point critique à partir duquel un petit choc local peut se propager à travers le réseau, et potentiellement conduire à des défaillances systémiques.

Modèles en cascade

Les modèles de cascade décrivent comment les défaillances (ou les informations) se propagent en cascade dans le réseau, en identifiant les voies de contagion et les points de vulnérabilité.

Les mathématiques dans la théorie de la percolation

Les mathématiques impliquent l'étude de la connectivité dans les graphes aléatoires à l'aide de :

Les processus stochastiques et les cascades
Lois d'échelle et exposants critiques
Universalité et théorie des groupes de renormalisation

Théorie des réseaux et percolation Applications en finance et trading

Évaluation du risque systémique

En analysant la structure du réseau financier, les régulateurs et les participants peuvent identifier les risques systémiques et les vulnérabilités.

Les nœuds à forte centralité peuvent être trop interconnectés, ce qui pose des risques de contagion en cas de défaillance.

Diversification du portefeuille

La théorie des réseaux peut aider les traders et les investisseurs à mieux comprendre l'interconnexion des actifs de leur portefeuille.

Elle permet une meilleure diversification en identifiant les actifs moins susceptibles d'être affectés par les mêmes chocs systémiques.

Prévision et gestion des crises

Les modèles de percolation peuvent simuler la façon dont les chocs se propagent dans les réseaux financiers, ce qui permet de prévoir les crises et d'élaborer des stratégies pour en atténuer l'impact.

Analyse de la structure des marchés

La compréhension de la structure en réseau des marchés peut révéler des schémas de flux d'informations, une segmentation du marché ou des risques de concentration.

Théorie des réseaux et percolation dans la crise financière de 2007-2008

La crise financière de 2007-2008 est une étude de cas convaincante pour l'application de la théorie des réseaux et de la percolation.

Au cours de cette période, les institutions financières étaient fortement endettées et interconnectées, et certaines avaient une exposition excessive à des instruments complexes tels que les titres adossés à des créances hypothécaires et les produits dérivés.

La théorie des réseaux explique comment ces connexions ont facilité la propagation rapide de la détresse du secteur des prêts hypothécaires à risque (c'est-à-dire trop de dettes concentrées et pas assez de revenus ou de nouveaux financements pour en assurer le service) aux marchés financiers mondiaux.

Cela a démontré le risque systémique posé par des réseaux financiers étroitement liés.

La théorie de la percolation permet de comprendre comment la défaillance d'institutions clés (nœuds) a entraîné un effet en cascade et a gravement compromis la stabilité du réseau.

La crise a souligné l'importance de comprendre les structures des réseaux et le "seuil de percolation", c'est-à-dire le point au-delà duquel des défaillances localisées peuvent risquer ou entraîner un effondrement systémique généralisé.

Cet événement a mis en évidence la nécessité de mieux analyser les réseaux financiers afin de prévoir et, espérons-le, de prévenir les effets de telles crises à l'avenir.

Comment les traders peuvent utiliser la théorie des réseaux et la percolation

Identifier les risques de corrélation et de contagion

Les traders peuvent utiliser l'analyse des réseaux pour identifier les actifs ou les secteurs susceptibles d'être affectés par la contagion - et donc de voir leurs risques sous-estimés.

Ils peuvent ainsi couvrir ou ajuster leurs positions en conséquence.

Placement stratégique des transactions

En comprenant la structure du réseau, les traders peuvent anticiper les mouvements potentiels du marché en fonction de l'emplacement et de l'influence des nœuds et des arêtes importants.

Analyse de la liquidité

Les modèles de réseau peuvent aider les traders à comprendre la dynamique de la liquidité sur le marché, c'est-à-dire à identifier les goulets d'étranglement potentiels ou les opportunités d'arbitrage.

Stratégies événementielles

En utilisant la théorie de la percolation, les traders peuvent modéliser l'impact probable d'événements spécifiques (par exemple, défaillances, changements de politique) sur le marché et ajuster leurs stratégies pour exploiter les mouvements anticipés.

Exemple de codage - Théorie des réseaux et percolation

Faisons un peu de code Python (avec l'aide de la bibliothèque Python networkx) pour montrer l'application de la théorie des réseaux et de la percolation dans un réseau financier synthétique.

Voici un bref aperçu des étapes et de l'observation initiale :

Création du réseau

Un réseau synthétique d'entités financières (comme des actions, des secteurs ou des banques) est généré à l'aide du modèle Erdos-Renyi.

Les nœuds représentent les entités et les arêtes symbolisent les relations financières.

Attribution d'attributs

Des poids aléatoires sont attribués aux :

aux nœuds (représentant l'importance du marché) et
arêtes (indiquant la force des relations financières)

Visualisation du réseau

Le réseau est ensuite visualisé.

Il présente les nœuds et les arêtes avec des tailles et des largeurs variables, proportionnelles à l'importance qui leur est attribuée et à la force des relations.

Plus grande composante connectée

Dans un premier temps, la taille de la plus grande composante connectée est identifiée. (Cela représente la robustesse du réseau de marché).

Dans le cas présent, avant toute suppression de nœud, la plus grande composante connectée comprend 29 nœuds sur 30, ce qui indique une connectivité élevée et une robustesse potentielle face à des défaillances isolées.

import networkx as nx
import matplotlib.pyplot as plt
import numpy as np

# Create synthetic financial network
# Nodes represent financial entities (e.g., stocks, sectors, banks)
# Edges represent financial relationships (e.g., ownership, correlation, lending)

G = nx.erdos_renyi_graph(30, 0.15)

# Assign random weights to nodes to represent their size or importance in the market
for node in G.nodes:
G.nodes[node]['size'] = np.random.randint(50, 1000)

# Assign random weights to edges to represent the strength of financial relationships
for edge in G.edges:
G.edges[edge]['weight'] = np.random.uniform(0.1, 1)

# Visualize the network
plt.figure(figsize=(12, 8))
pos = nx.spring_layout(G) # positions for all nodes

# Draw nodes with sizes proportional to their market importance
node_sizes = [G.nodes[node]['size'] for node in G.nodes]
nx.draw_networkx_nodes(G, pos, node_size=node_sizes, node_color="skyblue", alpha=0.6)

# Draw edges with widths proportional to the strength of financial relationships
edge_widths = [G.edges[edge]['weight'] for edge in G.edges]
nx.draw_networkx_edges(G, pos, width=edge_widths, alpha=0.4)

plt.title("Synthetic Financial Network")
plt.axis('off')
plt.show()

# Identify the largest connected component as a measure of market robustness
largest_cc = max(nx.connected_components(G), key=len)
print(f"Size of the largest connected component: {len(largest_cc)} / {G.number_of_nodes()}")

# Perform a basic percolation by progressively removing nodes and observing the effect on the network's connectivity
removed_nodes = 0
while len(largest_cc) > 1 and removed_nodes < len(G.nodes):
# Randomly remove a node
node_to_remove = np.random.choice(list(G.nodes))
G.remove_node(node_to_remove)
removed_nodes += 1

# Recalculate the largest connected component
if nx.is_connected(G):
largest_cc = max(nx.connected_components(G), key=len)
else:
break # Stop if the network becomes disconnected

print(f"After removing {removed_nodes} nodes, size of the largest connected component: {len(largest_cc)} / {G.number_of_nodes()}")

L'image générée à partir de ce code est la suivante (elle montre un nœud séparé du reste) :

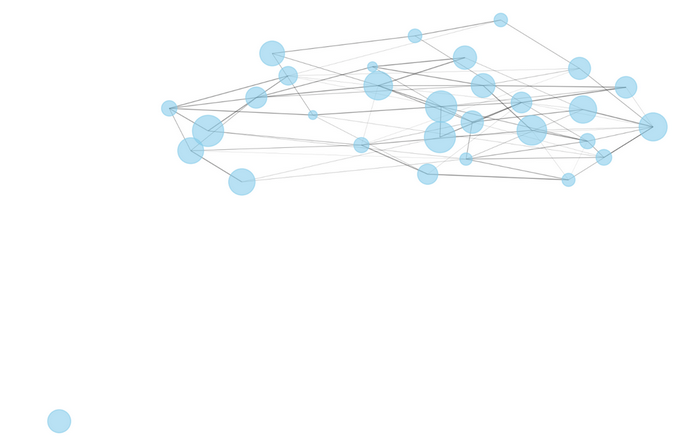
Réseau financier synthétique

Cette configuration permet d'étudier comment la percolation (c'est-à-dire la suppression progressive de nœuds) affecte la connectivité du réseau, un aspect important pour comprendre le risque systémique et la propagation des crises financières sur des marchés interconnectés.

Si nous faisions une analyse de percolation, cela impliquerait d'observer comment la suppression de nœuds (simulant des défaillances d'entités) a un impact sur la connectivité et la stabilité globales du réseau financier.

Exemple de codage - Analyse de percolation

Le code effectue une analyse de percolation sur un réseau financier synthétique.

Voici un résumé du processus et des résultats :

Réinitialisation du réseau

Un nouveau réseau Erdos-Renyi est généré pour simuler un réseau financier avec des connexions aléatoires entre les entités.

Processus de percolation

Des nœuds sont supprimés au hasard, un à la fois, pour simuler la défaillance ou le retrait d'entités financières du réseau.

Après chaque suppression, la taille de la plus grande composante connectée (indiquant le plus grand groupe d'entités interconnectées) est enregistrée.

Résultats de l'analyse

Le graphique que nous générons montre comment la taille de la plus grande composante connectée diminue au fur et à mesure que des nœuds sont supprimés.

Au départ, le réseau est robuste et présente une grande composante connectée.

Mais au fur et à mesure que des nœuds sont supprimés, la connectivité du réseau se détériore, ce qui démontre l'effet de percolation.

# Continued from previous setup for percolation analysis
G = nx.erdos_renyi_graph(30, 0.15)
for node in G.nodes:
G.nodes[node]['size'] = np.random.randint(50, 1000)

# Track the size of the largest connected component as nodes are removed
sizes_of_largest_component = [len(max(nx.connected_components(G), key=len))]

# Randomly remove nodes one by one and track the size of the largest connected component
np.random.seed(29) 
nodes_to_remove = np.random.permutation(G.nodes())
for node in nodes_to_remove:
G.remove_node(node)
if len(G) == 0: # If all nodes are removed, stop
break
largest_cc_size = len(max(nx.connected_components(G), key=len))
sizes_of_largest_component.append(largest_cc_size)

# Plot results of percolation analysis
plt.figure(figsize=(10, 6))
plt.plot(sizes_of_largest_component, marker='o', linestyle='-', color='b')
plt.title('Percolation Analysis in Financial Network')
plt.xlabel('Number of Nodes Removed')
plt.ylabel('Size of Largest Connected Component')
plt.grid(True)
plt.show()

Le graphique est présenté ci-dessous :

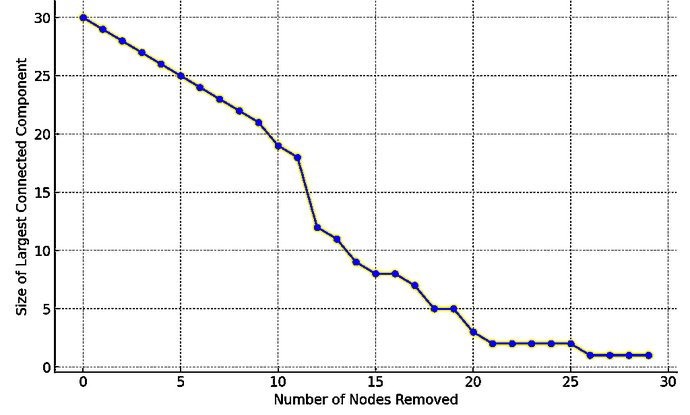
Effet de percolation dans un réseau financier

Résumé

Cette analyse aide à comprendre la résilience des réseaux financiers aux chocs.

Le point critique à partir duquel le réseau se désintègre (illustré par une forte diminution de la taille de la plus grande composante connectée) peut être considéré comme un seuil de risque systémique, au-delà duquel le réseau (ou le marché) ne peut plus fonctionner efficacement.

Conclusion

La théorie des réseaux et les modèles de percolation permettent de comprendre et d'exploiter les interdépendances des marchés financiers, principalement en ce qui concerne les entités qui y opèrent.

En s'appuyant sur ces concepts, les traders et les investisseurs peuvent mieux comprendre les risques systémiques, les modèles de corrélation et la dynamique générale du marché, ce qui peut les aider à prendre de meilleures décisions et à se positionner stratégiquement.

Néanmoins, ces modèles, même s'ils sont intéressants lorsqu'ils sont bien utilisés, sont des simplifications de la réalité et doivent être utilisés en conjonction avec d'autres outils d'analyse et la connaissance du marché.

Courtiers pour investir en bourse

Investir comporte des risques de perte

#1 17-02-2024 21:12:42