#1 20-02-2024 17:18:56

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 203

Processus Variance Gamma

Le processus Variance Gamma (VG) est un modèle mathématique utilisé sur les marchés financiers pour l'évaluation des options et pour saisir la dynamique des rendements des actifs.

Il est réputé pour sa capacité à modéliser l'asymétrie et la leptokurtose (queues grasses) observées dans la distribution des rendements - des caractéristiques souvent mal prises en compte par le modèle plus simple de Black-Scholes, qui suppose une distribution log-normale et une volatilité constante.

Le processus VG introduit des "sauts" dans les prix des actifs et une volatilité stochastique, ce qui offre une représentation plus précise des comportements du marché.

Principaux enseignements :

Capture les mouvements extrêmes

• Le processus Variance Gamma modélise la dynamique du marché, y compris les mouvements extrêmes rares mais impactants.

• Important pour les traders qui gèrent les risques de queue.

Incorpore la Skewness et la Leptokurtosis

• VG répond aux limites des modèles traditionnels en capturant la distribution asymétrique et à queue grasse des rendements.

• Permet une meilleure évaluation des prix et des risques.

Améliore la tarification des options

• Il fournit un cadre plus réaliste pour l'évaluation des options, en particulier pour les actifs avec des sauts observables et une volatilité variable.

Voici les concepts clés et les applications liés au processus VG :

Concepts clés du processus Gamma de variance

Volatilité stochastique et sauts

Contrairement aux modèles qui supposent une volatilité constante, le processus VG intègre à la fois la volatilité stochastique et les sauts dans les prix des actifs.

Il reflète plus précisément les observations empiriques des marchés financiers.

Processus Gamma

Le modèle VG est construit en subordonnant un mouvement brownien à un processus gamma.

Le processus gamma introduit l'élément "changement de temps", où la quantité de variance (volatilité) dans le mouvement brownien est elle-même aléatoire, modélisée par une distribution gamma.

Il en résulte un modèle qui peut produire des rendements présentant une asymétrie et une aplatissement.

Leptokurtose

Le processus VG est capable de capturer la leptokurtose, c'est-à-dire la présence de queues grasses dans la distribution des rendements.

Cela signifie qu'il peut modéliser plus précisément la probabilité de mouvements extrêmes sur le marché.

Skewness (asymétrie)

Le processus VG permet également de modéliser l'asymétrie dans la distribution des rendements, lorsque la distribution peut pencher vers des rendements plus positifs ou plus négatifs, une observation courante sur les marchés financiers réels.

Les mathématiques du processus Gamma de la variance

Voici un aperçu des mathématiques qui sous-tendent le processus Variance Gamma :

Idée maîtresse

Modéliser les rendements boursiers à l'aide d'un mouvement brownien dérivé subordonné à un processus Gamma.

• Xt = θGt + σW(Gt)

Où :

• Xt est le processus VG

• θ est le taux de dérive

• σ est la volatilité

• W(t) est un mouvement brownien

• Gt est un processus Gamma avec un taux moyen de 1/ν

Propriétés

• Conduit à des queues plus lourdes que le processus gaussien

• Permet une asymétrie et une aplatissement flexibles

• Possède des incréments indépendants et stationnaires

• Fonction caractéristique analytique

Utilisations mathématiques :

• Changements temporels et subordination des processus

• Propriétés du processus Gamma

• Fonctions caractéristiques et processus de Levy

Dans l'ensemble, les processus VG constituent un moyen simple d'introduire un comportement non gaussien dans les modèles de rendement des actifs à l'aide de la subordination probabiliste et des techniques de changement de temps.

Les mathématiques permettent d'ajuster les séries temporelles financières avec une flexibilité supplémentaire.

Applications du processus Gamma de variance

Fixation du prix des options

Le processus VG est largement utilisé pour l'évaluation des options européennes et exotiques, lorsque les modèles traditionnels tels que Black-Scholes ne parviennent pas à saisir les nuances du marché.

Il permet d'obtenir des prix plus précis en tenant compte de l'asymétrie et de l'aplatissement observés sur le marché.

Gestion du risque

En modélisant plus précisément les queues de la distribution des rendements, le processus VG permet de mieux quantifier et gérer le risque de mouvements extrêmes du marché, ce qui est important pour la gestion de portefeuille et la planification financière.

Analyse du marché

Les traders et les analystes utilisent les modèles VG pour évaluer la probabilité de sauts importants dans les prix des actifs.

Cela peut s'avérer essentiel pour les stratégies de négociation à court terme et pour la couverture contre les baisses de marché.

Titres à revenu fixe

Les processus de volatilité peuvent également être appliqués au marché des titres à revenu fixe pour évaluer les obligations et autres dérivés de taux d'intérêt, où les hypothèses de normalité et de volatilité constante ne sont généralement pas valables.

Trading de la volatilité

La capacité du modèle à intégrer la volatilité stochastique le rend utile pour négocier la volatilité en tant que classe d'actifs, par exemple par le biais d'options VIX, de swaps de variance et d'autres produits de volatilité.

Exemple de codage - Processus Variance Gamma

Prenons un exemple de codage d'un processus Variance Gamma.

import numpy as np
import matplotlib.pyplot as plt

# Paramètres pour le processus Variance Gamma
T = 1 # Time horizon
sigma = 0.12 # Volatility parameter for the Brownian motion part
nu = 0.1 # Rate of drift of the Variance Gamma process
theta = -0.14 # Drift of the Brownian motion part
gamma = 0.2 # Parameter to control the variance of the gamma process

# Paramètres temporels pour la simulation
N = 1000 # Number of steps
dt = T/N # Time step

# Simuler le processus Gamma de variance
# Étape 1 : Simuler le processus Gamma
t = np.arange(0, T, dt)
G = np.random.gamma(shape=dt/gamma, scale=gamma, size=N)

# Étape 2 : Simulation du mouvement brownien
W = np.random.normal(loc=0, scale=np.sqrt(dt), size=N)
X = theta*G + sigma*np.sqrt(G)*W + nu*G

# Calculer la somme cumulative pour obtenir les valeurs du processus
S = np.cumsum(X)

# Tracer le processus Variance Gamma
plt.figure(figsize=(10, 6))
plt.plot(t, S, label='Variance Gamma Process')
plt.title('Variance Gamma Process Simulation')
plt.xlabel('Time')
plt.ylabel('Process Value')
plt.legend()
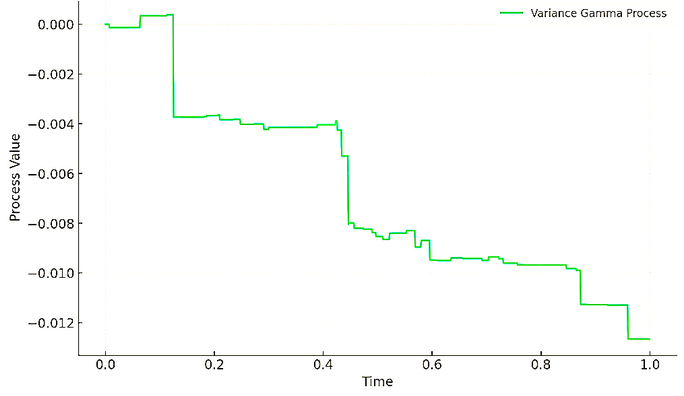
plt.show()

Le graphique tracé représente une simulation du processus Variance Gamma (VG) sur un horizon temporel de 1 an, en utilisant des paramètres spécifiés.

Dans cette simulation, le processus VG est caractérisé par :

• le paramètre de volatilité, σ=0,12

• taux de dérive, ν=0,1

• dérive de la partie mouvement brownien, θ=-0,14, et

• γ=0,2, contrôlant la variance du processus gamma.

La trajectoire résultante illustre la façon dont le processus VG peut modéliser la dynamique des prix des actifs avec des sauts.

Cela reflète son utilité pour capturer la leptokurtose et l'asymétrie observées dans les rendements des marchés financiers.

Solution du processus gamma de variance

Il peut s'agir, par exemple, d'un taux de change géré (c'est-à-dire ajusté périodiquement par les responsables politiques) :

• un taux de change géré (où il est périodiquement ajusté par les décideurs politiques)

• des niveaux de taux d'intérêt

• des évaluations d'actifs privés qui ne sont ajustées qu'occasionnellement

• certains types de produits dérivés

Conclusion

Le processus Variance Gamma permet de mieux comprendre le comportement des prix des actifs qui ne sont pas pris en compte par des modèles plus simples.

Sa capacité à modéliser la volatilité stochastique et les sauts en fait un modèle précieux pour l'évaluation des options, la gestion des risques et l'analyse des marchés dans différentes catégories d'actifs.

Brokers d'options

Investir comporte des risques de perte

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.