#1 16-01-2024 17:43:09

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 362

Optimisation multi-objectifs en finance, trading et marchés

L'optimisation multi-objectifs (MOO) fait référence aux processus mathématiques conçus pour optimiser simultanément plusieurs objectifs conflictuels.

Contrairement à l'optimisation mono-objectif, qui se concentre sur un seul objectif, l'optimisation multi-objectifs traite des scénarios dans lesquels des compromis doivent être faits entre deux ou plusieurs objectifs.

Cette complexité est courante dans des domaines tels que l'ingénierie, la finance, l'économie, l'élaboration de politiques et la logistique.

Principaux enseignements

Réalisation d'objectifs équilibrés

• L'optimisation multi-objectifs (MOO) en finance permet la poursuite simultanée de différents objectifs, tels que la maximisation des rendements et la minimisation des risques.

• Elle contribue à l'élaboration de stratégies d'investissement équilibrées.

Utilisation d'algorithmes avancés

• Utiliser des algorithmes, tels que les algorithmes génétiques et l'optimisation de Pareto, pour trouver efficacement des compromis entre des objectifs financiers contradictoires.

Prise de décision basée sur les données

• MOO intègre de vastes ensembles de données financières.

• Il améliore la précision de la prise de décision en matière de trading et d'analyse de marché en prenant en compte de multiples mesures de performance.

Exemple de codage

• Nous effectuons un type d'optimisation multi-objectif (optimisation de la moyenne, de la variance, de l'aplatissement et de l'asymétrie) dans un certain portefeuille ci-dessous.

Concepts fondamentaux

Objectifs et compromis

Dans la MOO, les objectifs représentent les différents buts à atteindre.

Ces objectifs sont souvent contradictoires, de sorte que l'amélioration de l'un d'entre eux peut en détériorer un autre.

Le défi principal consiste à trouver un équilibre ou un compromis entre ces objectifs concurrents.

Optimalité de Pareto

L'optimalité de Pareto est un concept clé de la MOO.

Une solution est optimale au sens du Pareto si aucun objectif ne peut être amélioré sans détériorer au moins un autre objectif.

L'ensemble des solutions optimales de Pareto forme le front de Pareto, qui est un outil de la MOO permettant de visualiser les compromis.

Espace de décision et espace d'objectifs

Deux espaces définissent la MOO :

• l'espace de décision et

• l'espace objectif

L'espace de décision contient toutes les solutions possibles, tandis que l'espace objectif associe ces solutions aux valeurs objectives correspondantes.

L'interaction entre ces espaces est fondamentale pour comprendre la MOO.

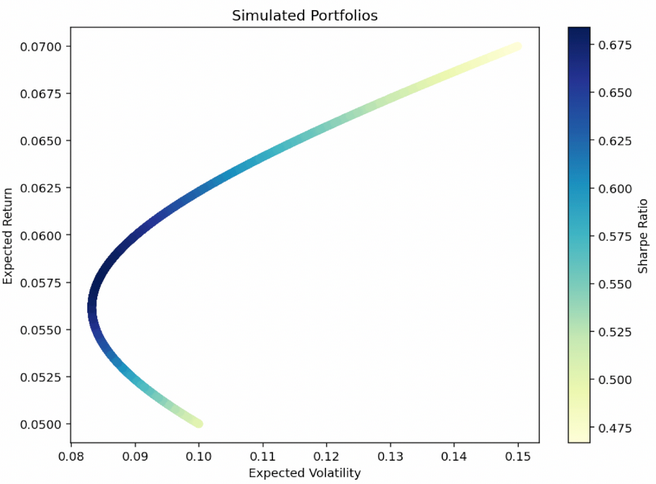
Le diagramme de la frontière d'efficacité pour l'optimisation de la moyenne-variance est un type d'exemple (la partie bleue la plus profonde du graphique représente la combinaison d'actifs la plus optimale) :

Méthodologies dans MOO

Techniques de scalarisation

La scalarisation consiste à convertir des objectifs multiples en un objectif unique, souvent par le biais de sommes pondérées.

Cette simplification permet d'utiliser les méthodes traditionnelles d'optimisation à objectif unique.

Mais elle nécessite une pondération minutieuse afin d'éviter tout biais en faveur de l'un ou l'autre objectif.

Algorithmes évolutifs

Les algorithmes évolutionnaires, comme les algorithmes génétiques, sont bien adaptés à la MOO en raison de leur capacité à explorer plusieurs solutions simultanément.

Ces algorithmes font évoluer les solutions au fil des générations et convergent idéalement vers le front de Pareto.

Prise de décision multicritères (analyse)

Les outils d'analyse décisionnelle multicritères (MCDA) aident à sélectionner la solution la plus appropriée sur le front de Pareto, en fonction des préférences et des priorités des parties prenantes.

Applications de l'optimisation multi-objectifs

Conception technique

En ingénierie, la MOO aide à concevoir des systèmes qui équilibrent le coût, l'efficacité et la performance.

Par exemple, dans la conception automobile, la MOO permet d'optimiser la consommation de carburant, la sécurité et le coût.

Optimisation des portefeuilles financiers

En finance, MOO est utilisé pour équilibrer le risque et le rendement dans la gestion de portefeuille.

Il s'agit de trouver un portefeuille qui offre le meilleur compromis entre les rendements attendus et les risques associés.

Il existe également le concept d'optimisation des moments supérieurs, tels que l'aplatissement et l'asymétrie.

Développement durable

Le MOO est utilisé dans le cadre du développement durable, où les objectifs environnementaux, économiques et sociaux doivent être équilibrés.

Il s'agit notamment d'optimiser l'utilisation des ressources tout en minimisant l'impact sur l'environnement et en maximisant le bien-être social.

Défis et orientations futures

Complexité informatique

La méthode MOO est très gourmande en ressources informatiques, en particulier lorsque le nombre d'objectifs augmente.

Le développement d'algorithmes plus efficaces est un domaine de recherche en cours.

Incertitude et robustesse

De nombreux problèmes du monde réel impliquent des inconnues dans les données et les paramètres du modèle.

L'amélioration de MOO pour gérer l'incertitude et fournir des solutions robustes est un axe de recherche clé.

Intégration interdisciplinaire

L'intégration de la MOO avec d'autres domaines, tels que l'apprentissage automatique et l'analyse de données, offre la possibilité de résoudre des problèmes d'optimisation de plus en plus complexes.

Exemple de codage - Optimisation multi-objectifs

Considérons l'optimisation d'un portefeuille en fonction de la moyenne, de la variance, de l'aplatissement et de l'asymétrie, sur la base des critères suivants :

• Actions : Rendement à terme de +6%, volatilité annualisée de 15% en utilisant l'écart type

• Obligations : Rendement à terme de +4 %, volatilité annualisée de 10 % en utilisant l'écart type

• Matières premières : Rendement à terme de +3%, volatilité annualisée de 15% en utilisant l'écart-type

• Or : +3% de rendement à terme, 15% de volatilité annualisée en utilisant l'écart-type +3% de rendement à terme, 15% de volatilité annualisée en utilisant l'écart-type

Pour créer une simulation de Monte Carlo en Python qui optimise un portefeuille pour la moyenne, la variance, l'aplatissement et l'asymétrie, en considérant les actifs donnés avec leurs rendements à terme et leurs volatilités, nous devons suivre les étapes suivantes :

• Générer des allocations de portefeuille aléatoires pour les actifs donnés.

• Calculer le rendement attendu, la variance, l'aplatissement et l'asymétrie du portefeuille (ou se contenter d'assigner des hypothèses, puisqu'il s'agit d'un exemple représentatif).

• Effectuer de nombreuses simulations pour trouver l'allocation optimale du portefeuille.

Voici un exemple de code Python pour y parvenir :

import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler

# Asset details
assets = {
"Stocks": {"return": 0.06, "volatility": 0.15, "skewness": 1, "kurtosis": 3},
"Bonds": {"return": 0.04, "volatility": 0.10, "skewness": 1, "kurtosis": 3},
"Commodities": {"return": 0.03, "volatility": 0.15, "skewness": 0, "kurtosis": 1},
"Gold": {"return": 0.03, "volatility": 0.15, "skewness": 1, "kurtosis": 1}
}

num_simulations = 10000
results = np.zeros((4, num_simulations))
weights_record = np.zeros((num_simulations, 4))

for i in range(num_simulations):
# Random allocations
weights = np.random.random(4)
weights /= np.sum(weights)
weights_record[i, :] = weights

# Portfolio metrics
portfolio_return = sum(weights * np.array([assets[a]["return"] for a in assets]))
portfolio_volatility = np.sqrt(sum((weights**2) * np.array([assets[a]["volatility"]**2 for a in assets])))
portfolio_skewness = sum(weights * np.array([assets[a]["skewness"] for a in assets]))
portfolio_kurtosis = sum(weights * np.array([assets[a]["kurtosis"] for a in assets]))

results[:, i] = [portfolio_return, portfolio_volatility, portfolio_skewness, portfolio_kurtosis]

results_frame = pd.DataFrame(results.T, columns=["Return", "Volatility", "Skewness", "Kurtosis"])

# Normalize the results to find the optimal portfolio
scaler = MinMaxScaler()
norm_results = scaler.fit_transform(results_frame)
norm_frame = pd.DataFrame(norm_results, columns=results_frame.columns)

# Optimizing for mean, variance, kurtosis, and skewness
# Higher mean and skewness, lower variance and kurtosis are preferred
optimal_idx = norm_frame['Return'].idxmax() - norm_frame['Volatility'].idxmin() + norm_frame['Skewness'].idxmax() - norm_frame['Kurtosis'].idxmin()

optimal_portfolio = results_frame.iloc[optimal_idx]
optimal_weights = weights_record[optimal_idx]
optimal_weights_df = pd.DataFrame(optimal_weights, index=["Stocks", "Bonds", "Commodities", "Gold"], columns=["Weight"])
optimal_weights_df.T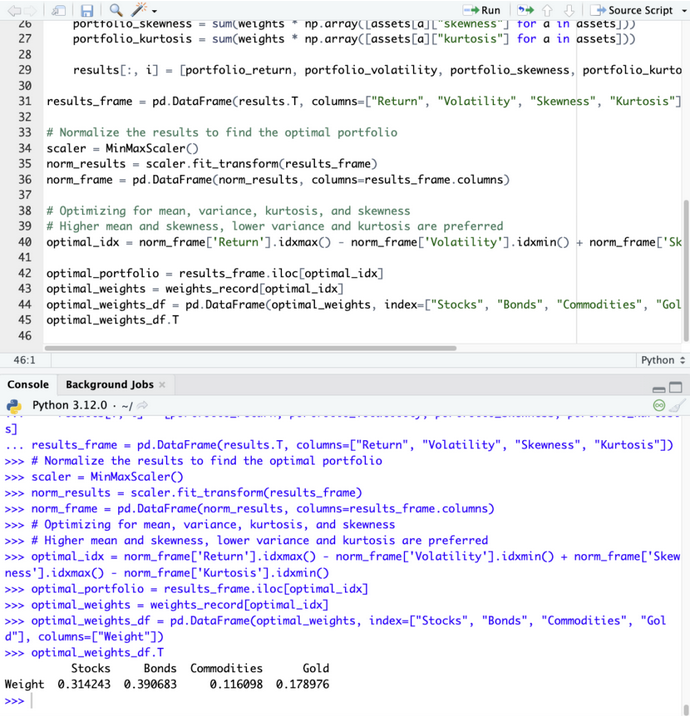

Nous constatons que l'allocation optimale pour cette optimisation multi-objectifs (moyenne, variance, kurtosis, skewness) est la suivante :

• Actions : 31.4%

• Obligations : 39.1%

• Matières premières : 11.6%

• Or : 17,9%

On peut aussi faire un diagramme :

# Optimal weights 

optimal_weights = [0.314243, 0.390683, 0.116098, 0.178976] 

assets = ["Stocks", "Bonds", "Commodities", "Gold"] 

# Creating a pie chart 

plt.figure(figsize=(8, 8)) 

plt.pie(optimal_weights, labels=assets, autopct='%1.1f%%', startangle=140) 

plt.title("Optimal Portfolio Allocation") 

plt.show()

Note : Ce code suppose que les actifs ne sont pas corrélés entre eux :

• Ce code suppose que les actifs ne sont pas corrélés.

• Toutes les mesures sont des hypothèses représentatives.

• La logique d'optimisation peut être ajustée en fonction de stratégies d'investissement spécifiques ou de préférences.

• Les scénarios réels peuvent nécessiter une gestion plus sophistiquée du risque et de la corrélation.

• Veillez à mettre ce code en retrait si vous l'utilisez vous-même (comme indiqué dans l'image ci-dessus).

Conclusion

L'optimisation multi-objectifs présente une approche sophistiquée pour traiter les problèmes du monde réel avec de multiples objectifs conflictuels.

Son application couvre de nombreux domaines, y compris la finance (par exemple, l'optimisation de portefeuille).

Elle offre un moyen structuré de trouver des compromis et de prendre des décisions en connaissance de cause.

L'évolution continue des méthodologies MOO et leur intégration avec d'autres technologies avancées promettent des capacités encore plus grandes dans la résolution de défis d'optimisation complexes.

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.