#1 23-09-2022 17:42:14

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 362

Règle empirique et son rôle dans le trading

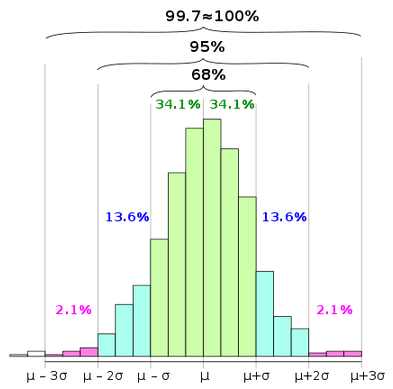
La règle empirique fait référence à la distribution normale et stipule que pour les données qui sont normalement distribuées, presque toutes les données se situent dans les trois écarts types de la moyenne.

En d'autres termes, si vous prenez une distribution normale et que vous la tracez sur un graphique, presque toutes les données se situeront dans les trois écarts types de la moyenne.

La règle empirique est aussi parfois appelée règle des 68-95-99,7 ou règle des trois sigmas.

Comment utilise-t-on la règle empirique ?

La règle empirique peut être utilisée pour déterminer la probabilité que quelque chose se produise.

Par exemple, si vous savez que la taille moyenne des personnes d'une certaine population est de 70 pouces, et que vous savez également que l'écart-type est de 3 pouces, vous pouvez utiliser la règle empirique pour déterminer combien de personnes de cette population sont susceptibles d'être plus grandes que 76 pouces.

Selon la règle empirique, environ 95 % des données se situent à moins de deux écarts types de la moyenne, ce qui signifie qu'environ 95 % des personnes de cette population ont une taille comprise entre 64 et 76 pouces.

De même, vous pouvez utiliser la règle empirique pour déterminer combien de personnes sont susceptibles d'être plus petites que 64 pouces ou plus grandes que 76 pouces.

Environ 2,5 % des données se situent en dehors de deux écarts types de la moyenne, ce qui signifie qu'environ 2,5 % des personnes de cette population seront plus petites que 64 pouces ou plus grandes que 76 pouces.

La règle empirique peut également être utilisée pour déterminer la probabilité qu'un événement se produise si vous connaissez la moyenne et l'écart type d'une population.

Par exemple, si vous savez que la note moyenne d'un test est de 80, et que vous savez également que l'écart-type est de 5, vous pouvez utiliser la règle empirique pour déterminer la probabilité qu'une personne obtienne une note de 90 ou plus à ce test.

Environ 95 % des données se situent à l'intérieur de deux écarts types de la moyenne, ce qui signifie qu'environ 95 % des personnes qui passent le test obtiendront une note comprise entre 70 et 90.

5 % des données se situeront en dehors de deux écarts types de la moyenne, ce qui signifie qu'environ 5 % des personnes qui passent le test obtiendront un score inférieur à 70 ou supérieur à 90.

La règle empirique peut être un outil utile pour comprendre les données, mais il est important de se rappeler que la règle ne s'applique qu'aux données qui sont normalement distribuées.

Toutes les données ne sont pas normalement distribuées et si vous essayez d'utiliser la règle empirique avec des données non normales, vous risquez d'obtenir des résultats inexacts.

La règle empirique et son rôle dans le trading

Certains événements sur les marchés sont souvent qualifiés d'"événements X-sigma", où X est un nombre entier représentant un certain écart-type.

Par exemple, s'il s'agit d'un "événement 3-sigma", cela signifie que 99,7% des données se produiront en dehors de ce qui s'est produit, ce qui le rend relativement rare.

De même, un "événement à 2 sigmas" serait un événement pour lequel 95 % des données se produiront en dehors de ce qui s'est produit, ce qui le rend moins rare.

Certains acteurs du marché pensent que certains événements sont si rares qu'ils ne peuvent être expliqués que par une forme d'intervention ou de manipulation (par exemple, par les banques centrales) et non par le fonctionnement naturel du marché.

La question de savoir si cela est vrai ou non est sujette à débat, mais la règle empirique peut être un outil utile pour comprendre la probabilité que certains événements se produisent.

Le problème de l'utilisation de la règle empirique sur les marchés financiers

La plupart des données de marché ont une queue de poisson, ce qui signifie que la distribution normale n'en est pas une bonne représentation.

La distribution normale a des queues fines, ce qui signifie qu'une fois que vous dépassez 3 écarts types, le modèle suggère que peu de données existent au-delà (c'est-à-dire seulement 0,3 % d'entre elles).

Dans ce cas, ce qui est considéré comme un "événement 7-sigma" (c'est-à-dire extrêmement rare) peut en fait ne pas être si rare que cela si les données qui y sont associées ne sont pas distribuées normalement.

Les événements rares ont tendance à se produire sur les marchés plus souvent que prévu, de sorte que les modèles financiers ne sont souvent pas construits avec l'hypothèse sous-jacente de normalité. Ils sont soit conçus sur mesure, soit construits à partir d'une base plus large, telle que la distribution t de Student.

C'est l'un des nombreux défis auxquels les traders et les investisseurs sont confrontés lorsqu'ils tentent de modéliser les marchés financiers.

Quels sont les avantages de l'utilisation de la règle empirique ?

Malgré les difficultés liées à l'utilisation de la règle empirique sur les marchés financiers, celle-ci présente tout de même certains avantages.

Le principal avantage est qu'elle peut vous aider à comprendre la probabilité que certains événements se produisent.

Cela peut être utile pour prendre des décisions de trading et d'investissement, car vous pouvez mieux comprendre la fréquence à laquelle un événement peut se produire.

Par exemple, si vous savez qu'une action a 1 % de chances d'augmenter de 5 % ou plus un jour donné, vous serez plus enclin à la trader si vous avez une stratégie qui tire profit des petits mouvements quotidiens.

En revanche, si vous savez qu'une action a 0,1 % de chances d'augmenter de 5 % un jour donné, vous serez peut-être moins enclin à la trader sur une période plus courte. En revanche, une action qui n'est pas volatile mais qui offre un rendement intéressant serait beaucoup plus intéressante pour un investisseur.

La règle empirique peut également vous aider à comprendre la distribution des données, ce qui peut être utile pour identifier les opportunités de trading.

L'utilisation de la règle empirique présente de nombreux autres avantages, mais ceux-ci sont parmi les principaux.

Conclusion - Règle empirique

Dans l'ensemble, la règle peut être un outil utile pour comprendre les données, mais il est important de se rappeler qu'elle a ses limites.

Plus précisément, la règle ne s'applique qu'aux données qui sont normalement distribuées, et la plupart des données de marché ne sont pas normalement distribuées.

Cela signifie que vous devez être prudent lorsque vous utilisez la règle sur les marchés financiers, car vous risquez de ne pas obtenir des résultats précis.

Malgré ses limites, la règle empirique peut être bénéfique à bien des égards, notamment en vous aidant à comprendre la probabilité que certains événements se produisent et à identifier les opportunités de trading.

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.