Vous n'êtes pas identifié(e).
- Contributions: Récentes | Sans réponse
#1 01-08-2023 15:59:07
- Climax
- Administrateur

- Inscription: 30-08-2008
- Messages: 6 411


Qu'est-ce que la convexité d'une obligation à coupon zéro ?
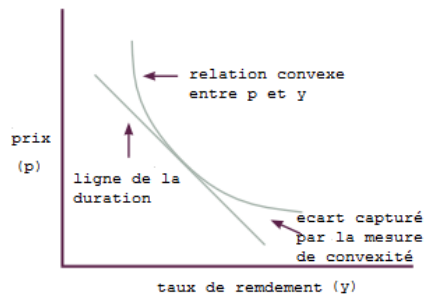
La convexité est une mesure de la courbure de la relation entre les prix et les rendements des obligations.
Elle montre comment la durée d'une obligation varie en fonction du taux d'intérêt.
Ce concept est particulièrement important dans le contexte des obligations à coupon zéro, qui sont des obligations qui ne paient pas d'intérêts pendant la durée de vie de l'obligation.
Les investisseurs achètent des obligations à coupon zéro avec une décote par rapport à leur valeur nominale, c'est-à-dire le montant qu'une obligation vaudra lorsqu'elle arrivera à échéance.
Le paiement prend plutôt la forme d'une appréciation du prix que de paiements de coupons.
Principaux enseignements :
➡️ La convexité est une mesure de la courbure de la relation entre les prix des obligations et les rendements obligataires, et elle montre comment la durée d'une obligation change lorsque le taux d'intérêt varie.
➡️ Les obligations à coupon zéro sont des instruments financiers uniques, émis avec une décote par rapport à leur valeur nominale et qui ne donnent pas lieu à des paiements d'intérêts périodiques. Leur convexité est plus élevée que celle des obligations à coupon de même échéance.
➡️ L'ajustement de convexité est important pour les obligations à coupon zéro en raison de leur convexité élevée. Il s'agit d'une correction appliquée au prix de l'obligation pour tenir compte de la convexité et qui peut affecter de manière significative le prix de l'obligation, en particulier lorsque les taux d'intérêt sont volatils.
➡️ La convexité d'une obligation à coupon zéro est le temps à courir jusqu'à l'échéance au carré.
➡️ Comprendre la convexité est très utile pour gérer le risque et prendre des décisions d'investissement éclairées.
Comprendre les obligations à coupon zéro
Les obligations à coupon zéro sont des instruments financiers uniques.
Elles sont émises avec une décote par rapport à leur valeur nominale et sont remboursées à leur valeur nominale à l'échéance.
La différence entre le prix d'achat et la valeur nominale représente le rendement de l'investisseur.
L'absence de paiements d'intérêts périodiques distingue les obligations à coupon zéro des obligations classiques.
La convexité et son importance
La convexité est une mesure de la sensibilité de la duration d'une obligation aux variations des taux d'intérêt.
En d'autres termes, elle mesure le taux de variation de la durée de l'obligation.
La convexité est un concept important dans la détermination du prix des obligations car elle permet aux opérateurs obligataires d'évaluer le risque associé aux variations des taux d'intérêt.
Convexité des obligations à coupon zéro
La convexité d'une obligation à coupon zéro est particulièrement intéressante.
Comme les obligations à coupon zéro n'effectuent pas de paiements d'intérêts périodiques, toute leur durée et leur convexité proviennent du paiement unique à l'échéance.
La convexité d'une obligation à coupon zéro est donc plus élevée que celle d'une obligation à coupon de même échéance.
Calcul de la convexité
La formule permettant de calculer la convexité d'une obligation est complexe et fait intervenir plusieurs variables, notamment le prix de l'obligation, son rendement et le temps écoulé jusqu'à chaque flux financier.
Pour les obligations à coupon zéro, la formule est simplifiée car il n'y a qu'un seul flux financier à l'échéance.
La convexité est la dérivée seconde du prix de l'obligation par rapport aux taux d'intérêt, tandis que la duration est la dérivée première.
Ajustement de la convexité
L'ajustement de convexité est une correction appliquée au prix d'une obligation pour tenir compte de la convexité de l'obligation.
Cet ajustement est particulièrement important pour les obligations à coupon zéro en raison de leur forte convexité.
L'ajustement de convexité peut affecter de manière significative le prix d'une obligation à coupon zéro, en particulier lorsque les taux d'intérêt sont volatils.
Exemple d'obligation à coupon zéro
Considérons une obligation à coupon zéro d'une valeur nominale de 1 000 dollars, avec un rendement annuel de 10 %.
L'obligation arrive à échéance dans cinq ans.
Prix
Ce prix représente le montant qu'un investisseur devrait payer pour acheter l'obligation aujourd'hui.
Dans le cas d'une obligation à coupon zéro, en raison de l'absence de paiement de coupon, il se calcule comme suit :
Le prix de l'obligation à coupon zéro d'une valeur nominale de 1 000 dollars, d'un rendement annuel de 10 % et d'une durée de 5 ans est d'environ 620,92 dollars.
Durée
La duration d'une obligation à coupon zéro est simplement sa durée jusqu'à l'échéance, qui est de 5 ans dans ce cas.
La duration est une mesure de la sensibilité du prix d'une obligation aux variations des taux d'intérêt.
Convexité
La mesure de convexité indique comment la durée de l'obligation varie en fonction du taux d'intérêt.
Elle montre comment la duration d'une obligation varie en fonction du taux d'intérêt.
Plus précisément, la convexité est le taux de variation de la duration le long de la courbe prix-rendement, et constitue donc une mesure de la sensibilité de l'obligation aux variations des taux d'intérêt.
Pour une obligation à coupon zéro, la formule de convexité est simplement le temps à courir jusqu'à l'échéance au carré. En effet, les flux de trésorerie d'une obligation à coupon zéro consistent en un paiement unique à l'échéance, de sorte que les calculs de la durée et de la convexité sont simples.
La raison pour laquelle il s'agit du temps à courir jusqu'à l'échéance au carré est due à la dérivation mathématique de la formule de convexité.
En général, la formule de convexité est la suivante :
Où :
P est le prix de l'obligation,
y est le rendement ou le taux d'intérêt,
n est le nombre de périodes,
Ct est le flux de trésorerie à la période t
Pour une obligation à coupon zéro, il n'y a qu'un seul flux financier à la fin de la période (à l'échéance), de sorte que la formule se simplifie à n∗(n+1), et comme n+1 est approximativement égal à n pour un grand n, elle se simplifie encore à n^2, qui est le temps à courir jusqu'à l'échéance au carré.
Plus la convexité est élevée, plus le prix de l'obligation est sensible aux variations des taux d'intérêt.
Cela peut être bénéfique dans un contexte de baisse des taux d'intérêt (car les prix des obligations augmenteront plus qu'ils ne le feraient pour une obligation ayant une convexité plus faible), mais peut également constituer un risque dans un contexte de hausse des taux d'intérêt (car les prix des obligations diminueront plus).
Résumé
Pour résumer :
Le prix de l'obligation à coupon zéro est d'environ 620,92 dollars.
La durée de cette obligation est de 5 ans.
La convexité de l'obligation est de 25.
Conclusion
Comprendre la convexité d'une obligation à coupon zéro est important pour les investisseurs et les traders.
Elle permet de savoir comment le prix de l'obligation évoluera en fonction des fluctuations des taux d'intérêt.
Cette connaissance peut aider les investisseurs à gérer le risque et à prendre des décisions d'investissement plus éclairées.
Courtiers pour investir en bourse
Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.
Hors ligne
- Utilisateurs enregistrés en ligne dans ce sujet: 0, invités: 1
- [Bot] ClaudeBot


