#1 23-09-2022 17:54:57

Climax

Administrateur

Inscription: 30-08-2008

Messages: 6 231

Régression linéaire multiple - Utilisation dans le trading

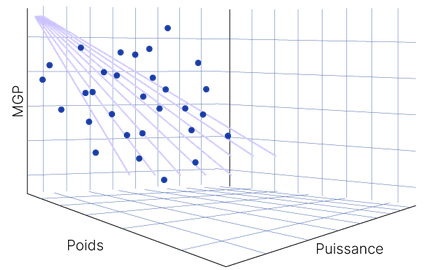
La régression linéaire multiple est une technique statistique utilisée pour prédire la valeur d'une variable dépendante (également appelée variable de résultat) en fonction des valeurs d'une ou plusieurs variables indépendantes (également appelées variables prédictives).

L'objectif de la régression linéaire multiple est de trouver la ligne ou la courbe la mieux ajustée qui représente la relation entre la variable dépendante et les variables indépendantes.

Afin de comprendre la régression linéaire multiple, il est important de comprendre d'abord la régression linéaire.

La régression linéaire

La régression linéaire est une technique statistique utilisée pour prédire la valeur d'une variable dépendante en fonction de la valeur d'une variable indépendante.

Par exemple, disons que vous souhaitez prédire le poids d'une personne en fonction de sa taille.

Dans ce cas, le poids serait la variable dépendante et la taille serait la variable indépendante.

Vous pouvez utiliser la régression linéaire pour trouver la ligne ou la courbe la mieux ajustée qui représente la relation entre le poids et la taille.

Une fois cette ligne ou cette courbe obtenue, vous pouvez l'utiliser pour prédire le poids d'une personne en fonction de sa taille.

La régression linéaire multiple est similaire à la régression linéaire, sauf qu'elle utilise plusieurs variables indépendantes au lieu d'une seule.

Dans ce cas, si vous vouliez prédire le poids d'une personne, vous n'utiliseriez pas seulement sa taille, mais aussi d'autres facteurs liés au mode de vie, etc.

Comment les modèles de régression multiple sont-ils utilisés en finance ?

Les modèles de régression multiple sont souvent utilisés en finance pour prédire la valeur future d'une variable dépendante (telle que le prix d'une action) en fonction des valeurs d'une ou plusieurs variables indépendantes (telles que d'autres prix d'actions).

Par exemple, supposons que vous souhaitiez prédire le prix futur de l'action de la société A sur la base des prix actuels de l'action de la société B et de l'action de la société C. Dans ce cas, le prix futur de l'action de la société A sera calculé à partir du prix de l'action de la société C.

Dans ce cas, le prix futur de l'action de la société A serait la variable dépendante et les prix actuels de l'action de la société B et de l'action de la société C seraient les variables indépendantes.

Vous pouvez utiliser la régression linéaire multiple pour trouver la ligne ou la courbe la mieux adaptée qui représente la relation entre le prix futur de l'action de l'entreprise A et les prix actuels de l'action de l'entreprise B et de l'action de l'entreprise C. Une fois que vous avez trouvé cette ligne ou cette courbe, vous pouvez la comparer à celle de l'action de l'entreprise C.

Une fois cette ligne ou cette courbe obtenue, vous pouvez l'utiliser pour prédire le prix futur de l'action de la société A en fonction des prix actuels de l'action de la société B et de l'action de la société C.

Il convient de noter que les modèles de ce type ne sont fiables que si toutes les variables ayant un impact sur le résultat sont incluses et si le passé est un bon prédicteur de l'avenir.

Lorsque ce n'est pas le cas, ces modèles peuvent donner de mauvais résultats.

Elle peut également aider à déterminer la force ou la faiblesse relative d'une relation.

Par exemple, si vous voulez déterminer les facteurs qui influencent le prix des actions d'un mineur d'or, vous pouvez utiliser le prix au comptant de l'or et le taux d'inflation. (Le taux d'inflation peut être un indicateur utile pour déterminer l'assouplissement ou le resserrement relatif de la politique monétaire qui, à son tour, oriente les flux de monnaie et de crédit).

Exemple : Modèle Fama-French

Le modèle à trois facteurs de Fama-French est un modèle de régression multiple qui décrit les rendements des actions en fonction de trois facteurs :

• le risque de marché

• le risque de taille, et

• risque lié à la valeur

Le modèle a été développé par Eugene Fama et Kenneth French en 1990.

Le facteur de risque du marché est le rendement du portefeuille du marché. Le facteur de risque lié à la taille est le rendement d'un portefeuille composé de petites actions moins le rendement d'un portefeuille composé de grandes actions.

Le facteur de risque lié à la valeur est le rendement d'un portefeuille composé d'actions à ratio comptable élevé par rapport au marché, moins le rendement d'un portefeuille composé d'actions à faible ratio comptable par rapport au marché.

Il a été démontré que le modèle à trois facteurs de Fama-French explique une part importante de la variation des rendements boursiers. Il s'agit d'un modèle populaire pour la recherche universitaire et il a été utilisé dans une variété d'applications.

Ces dernières années, le modèle a fait l'objet de critiques, certains estimant qu'il ne reflète pas fidèlement la véritable nature des rendements boursiers.

Cependant, le modèle reste un outil utile pour comprendre les moteurs des rendements boursiers.

Modèles dérivés de Fama-French

Depuis la publication du modèle original à 3 facteurs, un certain nombre de modèles dérivés ont été développés.

L'idée est que le modèle à 3 facteurs ne tient pas compte de toutes les variables et qu'il peut être amélioré.

Le plus notable d'entre eux est le modèle à quatre facteurs de Carhart, qui ajoute un facteur de momentum au modèle à trois facteurs de Fama-French.

Parmi les autres modèles dérivés, citons le modèle à cinq facteurs, le modèle à six facteurs et le modèle à sept facteurs.

Il a été démontré que le modèle à quatre facteurs de Carhart fournit une meilleure explication des rendements boursiers que le modèle original à trois facteurs de Fama-French.

Cependant, la question de savoir si les facteurs supplémentaires améliorent réellement le pouvoir explicatif du modèle ou s'ils capturent simplement des facteurs de risque connus d'une manière différente fait débat.

Le modèle à trois facteurs de Fama-French continue d'être un outil utile pour comprendre les rendements boursiers et devrait rester un élément important de la recherche financière dans les années à venir.

Quels sont les avantages de l'utilisation de la régression linéaire multiple ?

L'utilisation de la régression linéaire multiple présente de nombreux avantages, notamment :

1. La régression linéaire multiple peut être utilisée pour prédire la valeur d'une variable dépendante en fonction des valeurs d'une ou plusieurs variables indépendantes.

2. La régression linéaire multiple peut être utilisée pour trouver la ligne ou la courbe la mieux ajustée qui représente la relation entre la variable dépendante et les variables indépendantes.

3. La régression linéaire multiple peut être utilisée pour déterminer la force ou la faiblesse relative de la relation entre la variable dépendante et les variables indépendantes. 4.

4. La régression linéaire multiple peut être utilisée pour évaluer l'impact de plusieurs variables indépendantes sur une variable dépendante. 5.

5. La régression linéaire multiple peut être utilisée pour identifier les variables indépendantes qui sont les plus importantes pour prédire la valeur d'une variable dépendante.

Quelles sont les limites de l'utilisation de la régression linéaire multiple ?

L'utilisation de la régression linéaire multiple présente plusieurs limites, notamment :

1. La régression linéaire multiple exige que toutes les variables ayant un impact sur les résultats soient incluses dans le modèle. Si des variables importantes sont omises, les résultats de la régression linéaire multiple seront inexacts.

2. La régression linéaire multiple ne fonctionne que si le passé est un bon prédicteur de l'avenir. Si les variables incluses dans le modèle ne sont pas de bons prédicteurs de la variable dépendante, les résultats de la régression linéaire multiple ne seront pas précis.

3. La régression linéaire multiple peut être affectée par des valeurs aberrantes, ou des points de données qui sont éloignés du reste des données. Les valeurs aberrantes peuvent avoir un impact significatif sur les résultats d'une régression linéaire multiple et doivent être supprimées de l'ensemble des données si possible.

4. La régression linéaire multiple peut être affectée par la multicollinéarité, c'est-à-dire lorsque deux variables indépendantes ou plus sont fortement corrélées entre elles. Cela peut poser des problèmes car il peut être difficile de déterminer quelle variable indépendante a le plus grand impact sur la variable dépendante.

5. La régression linéaire multiple peut être affectée par l'hétéroscédasticité, c'est-à-dire lorsque la variance de la variable dépendante n'est pas constante pour toutes les valeurs des variables indépendantes. Cela peut poser des problèmes car il peut être difficile d'interpréter avec précision les résultats de la régression linéaire multiple.

Différence entre la régression linéaire et la régression multiple

La principale différence entre la régression linéaire et la régression multiple est que la régression linéaire utilise une seule variable indépendante pour prédire la valeur d'une variable dépendante, tandis que la régression multiple utilise deux variables indépendantes ou plus pour prédire la valeur d'une variable dépendante.

La régression linéaire et la régression multiple sont toutes deux des outils utiles pour l'analyse prédictive.

Cependant, la régression multiple est généralement plus précise que la régression linéaire car elle peut prendre en compte les relations entre plusieurs variables indépendantes et la variable dépendante.

Naturellement, il y a souvent plus d'une entrée qui affecte une sortie.

Par exemple, si l'on souhaite prédire le taux d'inflation par régression multiple, les entrées peuvent être les suivantes

• Le taux de chômage

• Divers taux d'intérêt (par exemple, taux à court terme, taux à 10 ans, taux hypothécaire à 30 ans)

• Le taux de croissance de l'économie

• Le prix du pétrole, des produits de base et d'autres intrants industriels.

Chacun de ces éléments aura un certain effet sur l'inflation, mais ils n'auront pas un effet égal. Il est donc important d'utiliser la régression multiple afin de déterminer l'importance relative de chaque facteur.

En outre, la régression multiple peut également tenir compte des relations non linéaires entre les variables indépendantes et la variable dépendante.

Conclusion - Régression linéaire multiple

La régression linéaire multiple est une technique statistique qui est utilisée pour estimer les relations entre une variable de réponse et une ou plusieurs variables prédictives.

La variable de réponse est également appelée variable dépendante, et la variable prédictive est également appelée variable indépendante.

La régression linéaire multiple peut être utilisée pour estimer les relations entre une variable de réponse et un ensemble de variables prédictives, qui peuvent être continues ou catégoriques.

Les estimations de coefficient produites par la régression linéaire multiple sont utilisées pour déterminer la force des relations entre la variable de réponse et les variables prédictives, et si ces relations sont statistiquement significatives.

La régression linéaire multiple peut être utile en finance car elle peut être utilisée pour estimer les relations entre les résultats (par exemple, les rendements boursiers) et un ensemble de variables prédictives, telles que le rendement du marché, la taille, la valeur, le momentum et la volatilité.

Les estimations des coefficients peuvent être utilisées pour prendre des décisions d'investissement, par exemple pour décider quelles actions acheter ou vendre, et quand les acheter ou les vendre.

---

Le trading de CFD implique un risque de perte significatif, il ne convient donc pas à tous les investisseurs. 74 à 89% des comptes d'investisseurs particuliers perdent de l'argent en négociant des CFD.